Application of the finite segment method to stabilisation of the force in a riser connection with a wellhead

Abstract

This paper presents a spatial model of riser dynamics formulated using the segment method and its applications. The model has been validated by comparison of the authors’ own results with those obtained from experimental measurements and Abaqus on the basis of forced vibration with large amplitude for the riser submerged in water. The influence of the sea environment is considered. Correctness and numerical effectiveness of the model enable us to formulate and solve the force stabilisation problem. A dynamic optimisation problem is formulated and solved. As a result vertical courses of movement of the upper end of the riser are obtained which compensate the horizontal movement of the base and stabilise the force in the connection of the riser with a wellhead.

1 Introduction

Deep sea drilling for hydrocarbons requires the use of very sophisticated technical equipment. Thus complex computational methods are used in the design phase of offshore devices. Calculation of statics and dynamics of risers is an important element of this process and is carried out before production. Risers are long elements with bending and longitudinal flexibilities; these risers are loaded with significant forces acting at their ends and large transverse forces caused by sea currents and hydrodynamic forces. Deflections of risers can be very large, and they may undergo elastoplastic deformations [1].

For modelling such structures as risers, the finite element method is used most often [2], which is reflected in many software packages like ANSYS, Abaqus or Riflex. However, many other methods are also used: finite difference method [3], lumped-mass method [4,5,6], finite segment method [7,8,9,10], or the similar rigid finite element method [11,12,13,14,15,16]. Most of the methods mentioned use Morison equations in order to describe the influence of the sea.

In this paper, we present the authors’ own formulation of the finite segment method for discretisation of a link with bending flexibility. The finite segment method has been used in modelling risers and cables for more than 50 years [7, 10, 17]. Its main idea lies in dividing a slender link into rigid elements connected by spherical joints treated as massless spring-damping elements in order to reflect torsional and bending flexibilities, and sometimes also longitudinal flexibility of the discretised links [18]. A similar approach derived from the rigid finite element method [19, 20] is used by Drąg [15, 16].

The finite segment method belongs to a group of methods used for dynamic analysis of slender systems, in which a continuous system is replaced by a system of rigid bodies reflecting inertial features of the system modelled. These rigid bodies are not point masses as in the lumped-mass method, but elements (segments) for which masses and moments of inertia are accurately determined. Using this method, it is not necessary to formulate partial differential equations for dynamics, but the equations of motion are usually derived from the Lagrange equations by means of multibody-system techniques. The choice of generalised coordinates is an important issue. Drąg in his papers [15, 16] uses absolute coordinates, which are three translational coordinates (describing the position of the chosen point of each rigid element) and up to three rotational coordinates describing the orientation of the rigid element. The translational coordinates are then eliminated by introducing reactions and constraint equations. The advantage of using the absolute coordinates is a pseudo-diagonal mass matrix, while the large number of coordinates and the necessity of stabilisation of constraint equations are disadvantages of the method. In the paper, we propose to use joint coordinates. In this case, the vector of generalised coordinates has a minimum number of components; these components are three coordinates of a chosen point of the link discretised and up to a three coordinates describing the orientation of each segment. This means that it is not necessary to introduce reactions and formulate constraint equations. Consequently, there is no need to stabilise the geometrical constraint equations as in the case of absolute coordinates. However, the disadvantage of the method is a full mass matrix. When large deformations are analysed, the mass matrix obtained using both approaches depends on generalised coordinates. In general, the finite segment method with the use of joint coordinates is more numerically effective for a moderate number of segments (less than 100) than when the absolute coordinates are used.

The finite segment method is admittedly not in all respect more efficient than the finite element method applied in commercial software packages, including those for simulation of statics and dynamics of offshore appliances. However, as far as analysis of slender links (cables, risers) is concerned, the finite segment method poses important advantages, such as simple physical interpretation, the ease of describing large deformations of links, and the possibility of special applications, including those presented in the paper.

The authors’ formulation of the finite segment method is implemented and validated by comparison of their own results with those presented by other researchers, especially those using experimental measurements, as well as with results obtained using professional software. Two experiments are considered—one examines natural frequencies of a riser under different tensions [21, 22], and the other is concerned with measurements of vibrations caused by oscillatory motion of the upper end of the riser [23,24,25]. Another method of validation is to compare the results of authors’ own calculations for forced vibrations of a riser with those obtained from Abaqus. In all cases of validation, good compatibility of results has been achieved. The validated model is then used to stabilise the force in the connection between the riser and a wellhead. The problem is formulated as a dynamic optimisation problem. The aim is to choose vertical displacements of the upper end of the riser which, despite the horizontal movement of the base (platform or vessel) and sea current, ensure that the force in the connection of the riser and the wellhead is kept as close as possible to the static position. It is assumed that the base follows a path on a surface [26]. The considerations are limited to compensation of horizontal movements of the upper end of the riser, since compensation of vertical movements is not difficult [16]. Optimisation calculations are carried out for an almost straight riser. The results obtained are interesting due to the possibility of the method presented being used for preparation of learning sets for ANN (artificial neural network) and its potential application to control of HCS (heave compensation system).

Fig. 1

Flexible link a before and after deformation, b its discretisation

Analysis of literature concerned with modelling of risers shows that most attention is devoted to analysis of static deflections and bending vibrations both in 2D and 3D analysis. Some research, however, shows that it is necessary to consider torsion. For example, [5, 27] demonstrate how to take into account the bending–torsion coupling effect, especially in the case of seabed interaction. The finite segment formulation presented in this paper, similar to [25, 28,29,30], omits the torsional flexibility of the riser model.

Most papers dealing with modelling of risers consider longitudinal flexibility. Consideration of elongation of slender systems is especially necessary when the analysis is concerned with top-tensioned risers or catenary lines. The elongation of the riser (500 m long) considered in this paper does not exceed 3 cm. This means that the influence of longitudinal deformations on displacements of the riser is negligible, which is why considerations in this paper are limited to analysis of spatial bending vibrations. Consequently, forces acting at the ends of the riser can be calculated in a different way (to be explained in Sect. 2).

2 Model of a slender link using the finite segment method

The basic idea of the finite segment method lies in the discretisation of a flexible link into rigid elements (segments) reflecting inertial features of the link. The segments are connected by means of joints consisting of massless and nondimensional spring-damping elements reflecting stiffness characteristics of the link (Fig. 1).

When the longitudinal flexibility is omitted, the following relation is true:

$$\begin{aligned} L={\widehat{P_0 P_n}}=\mathop \sum \limits _{i=0}^n l_i \end{aligned}$$

(1)

This means that the length of the deformed link along its curvature is constant and it enables quantity $\Delta$ shown in Fig. 1a, caused by large deformations of the flexible link, to be taken into account. In order to define the position of any point lying on a neutral axis of the link in segment i, notation presented in Fig. 2 is introduced.

The position of point P of segment i lying at distance $\xi$ from point $P_i$ depends on orientation of axes of reference coordinate system $\left\{ i \right\}$ with respect to axes of inertial frame of reference $\{ \}$.

Fig. 2

Segment i—notation used

In this paper, Euler angles ZYX presented in Fig. 3 are used. These angles define absolute rotations, in contrast to other papers [7, 18], in which Euler angles ZYX define orientation of system $\left\{ i\right\}$ with respect to the preceding segment $\left\{ {i-1} \right\}$ .

Fig. 3

Euler angles ZYX

The order of rotations which leads the end of segment i from position $P_{i+1}^0$ (when segment $P_i P_{i+1}^0$ is parallel to axis x of the inertial frame) to position $P_{i+1}$ is as follows:

• first rotation about axis $z^{{\prime }}$ parallel to z of angle $\psi _i$,

• then rotation about axis ${y}^{\prime \prime }$ of angle $\theta _i$,

• finally rotation of angle $\varphi _i$ about axis $x_i^{\prime }$ if torsion is considered.

It should be noted that the rotations are performed about axes assigned to the segment. Such angles of rotations are often used in airplane mechanics and are called heading, attitude and bank angles [31].

Coordinates of point P of segment i can be defined by the formula:

$$\begin{aligned} \mathbf{r}_i = \mathbf{r}_{P_i } +\mathbf{R}_i \mathbf{r}_{\varvec{i}}^{\prime } \end{aligned}$$

(2)

where $\mathbf{r}_{P_i }$ are coordinates of point $P_i$, $\mathbf{R}_i =\mathbf{R}_{\psi _i } \mathbf{R}_{\theta _i } \mathbf{R}_{\varphi _i }$, $\mathbf{R}_{\psi _i } {=}\left[ {{\begin{array}{ccc} {c\psi _i }&{}\quad {-s\psi _i }&{}\quad 0 \\ {s\psi _i }&{} \quad {c\psi _i }&{}\quad 0 \\ 0&{} \quad 0&{}\quad 1 \\ \end{array} }} \right]$, $\mathbf{R}_{\theta _i } {=}\left[ {{\begin{array}{ccc} {c\theta _i }&{}\quad 0&{}\quad {s\theta _i } \\ 0&{} \quad 1&{} \quad 0 \\ {-s\theta _i }&{} \quad 0&{}\quad {c\theta _i } \\ \end{array} }} \right] , \mathbf{R}_{\varphi _i } =\left[ {{\begin{array}{ccc} 1&{} \quad 0&{} \quad 0 \\ 0&{}\quad {c\varphi _i }&{}\quad {-s\varphi _i } \\ 0&{} \quad {s\varphi _i }&{}\quad {c\varphi _i } \\ \end{array} }} \right] , c\alpha _i =\hbox {cos}\alpha _i , s\alpha _i =\hbox {sin}\alpha _i , \alpha _i \in \left\{ {\psi _i ,\theta _i ,\varphi _i } \right\} , \mathbf{r}_i^{\prime } =\left[ {{\begin{array}{ccc} \xi &{}\quad 0&{}\quad 0 \\ \end{array} }} \right] ^{T}$.

In further consideration, torsion is omitted (angles $\varphi _i \equiv 0)$ and thus rotation matrices $\mathbf{R}_i$ take the following form:

$$\begin{aligned} \mathbf{R}_i =\mathbf{R}_{\psi _i } \mathbf{R}_{\theta _i } \end{aligned}$$

(3)

If we assume that points $P_0, \ldots , P_n$ lie on the neutral axis of the link, then coordinates of point $P_i$ can be defined as follows:

$$\begin{aligned} \mathbf{r}_{P_i } =\mathbf{r}_0 +\mathop \sum \limits _{j=0}^{i-1} l_j {\varvec{\upphi }} _j \end{aligned}$$

(4)

where ${\varvec{\upphi }} _j =\left[ {{\begin{array}{c} {c\psi _j c\theta _j } \\ {s\psi _j c\theta _j } \\ {-s\theta _j } \\ \end{array} }} \right]$ is the first column of matrix $\mathbf{R}_j$, and coordinates of point P are defined by the relation:

$$\begin{aligned} \mathbf{r}_i =\mathbf{r}_0 +\mathop \sum \limits _{j=0}^{i-1} l_j {\varvec{\upphi }} _j +\xi {\varvec{\upphi }} _i \end{aligned}$$

(5)

The system of segments $0,\ldots , n$ is defined by components of the vector with $N=3+2\left( {n+1} \right)$ elements:

$$\begin{aligned} {\mathbf{q}} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{r}}_0}}\\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\mathbf{q}}_0}}\\ \vdots \end{array}}\\ {{{\mathbf{q}}_i}}\\ {\begin{array}{*{20}{c}} \vdots \\ {{{\mathbf{q}}_n}} \end{array}} \end{array}} \end{array}} \right] \end{aligned}$$

(6)

where $\mathbf{r}_0 =\left[ {{\begin{array}{l} {x_0 } \\ y \\ {z_0 } \\ \end{array} }} \right]$ is the vector of coordinates of point $P_0$, $\mathbf{q}_i =\left[ {{\begin{array}{l} {\psi _i } \\ {\theta _i } \\ \end{array} }} \right]$ is the vector of coordinates describing relative motion of the $i\hbox {th}$ segment.

The equations of motion are derived from the Lagrange equations:

$$\begin{aligned} \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{q}}_j}}} {-} \frac{{\partial T}}{{\partial {q_j}}} {+} \frac{{\partial V}}{{\partial {q_j}}} + \frac{{\partial D}}{{\partial {{\dot{q}}_j}}} = {Q_j}, \,\mathrm{for }\,\,j = 1, \ldots ,N\nonumber \\ \end{aligned}$$

(7)

where T is kinetic energy of the link, V is the potential energy of the link, D is the function describing dissipation of energy (damping), $q_j, {\dot{q}}_j$ are generalised coordinates and velocities, respectively, $Q_j$ are generalised forces and N is the number of generalised coordinates.

The kinetic energy of the i-th segment is defined by the following expression:

$$\begin{aligned} {T_i} = \rho {A_i}\mathop \int \nolimits _0^{{l_i}} {\dot{\mathbf{r}}}_i^T{{\dot{\mathbf{r}}}_i}d\xi \end{aligned}$$

(8)

where $\rho$ is the material density, $A_i$ is the cross-sectional area of segment i.

When the riser is filled with fluid, and the added mass of water for a segment submerged is considered, the following takes place:

$$\begin{aligned} \rho A_i =\varrho _r A_{i,r} +\varrho _F A_{i,inn} +\varrho _w \left( {c_M -1} \right) A_{i,out} \end{aligned}$$

(9)

where $A_{i,r}$ is the cross-sectional area of the riser, $A_{i,inn}$ is the internal cross-sectional area of the riser, $A_{i,out}$ is the external cross-sectional area of the riser, $\varrho _r$ is the material density of the riser, $\varrho _F$ is the density of the fluid filling the riser, $\varrho _w$ is the density of water, $c_M$ is the inertial coefficient.

Having taken into account (5) after some transformations, energy $T_i$ can be expressed in the form:

$$\begin{aligned} {T_i}= & {} \frac{1}{2}{m_i}{\dot{\mathbf{r}}}_0^T{\dot{\mathbf{r}}_0} + {m_i}{\dot{\mathbf{r}}}_0^T\mathop \sum \limits _{j = 0}^i {b_{ij}}{\dot{\varvec{\upphi }} _i} \nonumber \\&+ \frac{1}{2}{m_i}\mathop \sum \limits _{j = 0}^i \dot{\varvec{\upphi }}_j^T\mathop \sum \limits _{k = 0}^i {d_{ijk}}{\dot{\varvec{\upphi }} _k} \end{aligned}$$

(10)

where $b_{ij} =\left\{ {{\begin{array}{ll} l_j&{} \quad \hbox {if }\,j<i \\ \frac{l_i }{2} &{} \quad \hbox {if }\,j=i \\ \end{array} }} \right. , d_{ijk} =\left\{ {\begin{array}{ll} b_{ij} b_{ik} &{}\hbox { if }j<i\, \hbox {or }\,k<i \\ \frac{1}{3}l_i^2&{} \hbox { if }j=i=k \\ \end{array} } \right.$, $m_i =\rho A_i l_i , m=\mathop \sum \nolimits _{j=0}^n m_j$.

The kinetic energy of the whole link can be written in the following form:

$$\begin{aligned} T= & {} \mathop \sum \limits _{i = 0}^n {T_i} = \frac{1}{2}m{\dot{\mathbf{r}}}_0^T{{\dot{\mathbf{r}}}_0} + {\dot{\mathbf{r}}}_0^T\mathop \sum \limits _{i = 0}^n {m_i}\mathop \sum \limits _{j = 0}^i {b_{ij}}{\dot{\varvec{\upphi }} _i} \nonumber \\&+\, \frac{1}{2}\mathop \sum \limits _{i = 0}^n {m_i}\mathop \sum \limits _{j = 0}^i \dot{\varvec{\upphi }} _j^T\mathop \sum \limits _{k = 0}^i {d_{ijk}}{\dot{\varvec{\upphi }} _k} \end{aligned}$$

(11)

where $m=\mathop \sum \nolimits _{i=0}^n m_i$ is the mass of the link.

The following identities can be proved by induction:

$$\begin{aligned}&\mathop \sum \limits _{i = 0}^n {m_i}\mathop \sum \limits _{j = 0}^i {b_{ij}}{\dot{\varvec{\upphi }} _i} = \mathop \sum \limits _{i = 0}^n { \bar{b}_i}{\dot{\varvec{\upphi }} _i} \end{aligned}$$

(12a)

$$\begin{aligned}&\mathop \sum \limits _{i = 0}^n {m_i}\mathop \sum \limits _{j = 0}^i \dot{\varvec{\upphi }} _j^T\mathop \sum \limits _{k = 0}^i {d_{ijk}}{\dot{\varvec{\upphi }} _k} = \mathop \sum \limits _{i = 0}^n \dot{\varvec{\upphi }} _i^T\mathop \sum \limits _{j = 0}^n {\bar{d}_{ij}}{\dot{\varvec{\upphi }} _j} \end{aligned}$$

(12b)

where ${\bar{b}} _i =\mathop \sum \nolimits _{j=i}^n m_j b_{ji}$, ${\bar{d}} _{ij} =\mathop \sum \nolimits _{l={\mathrm{max}}\left\{ {i,j} \right\} }^n m_l d_{lij}$.

In view of (12), the kinetic energy can be expressed as follows:

$$\begin{aligned} T= & {} \frac{1}{2}m{\dot{\mathbf{r}}}_0^T{{\dot{\mathbf{r}}}_0} + {\dot{\mathbf{r}}}_0^T\mathop \sum \limits _{i = 0}^n {m_i}{{\bar{b}}_i}{\dot{\varvec{\upphi }}_i} \nonumber \\&+\, \frac{1}{2}\mathop \sum \limits _{i = 0}^n \dot{\varvec{\upphi }} _i^T\mathop \sum \limits _{j = 0}^n {\bar{d}_{ij}}{\dot{\varvec{\upphi }} _j} \end{aligned}$$

(13)

It should be noted that coefficients ${\bar{b}}_i$ and ${\bar{d}} _{ij}$ are constant.

After differentiating ${\varvec{\upphi }}_i$ defined by (4) with respect to time t, the following is obtained:

$$\begin{aligned}&{\dot{\varvec{\upphi }} _i} = {\dot{{\psi }} _i}{{\varvec{\upphi }} _{i,\psi }} + {\dot{\theta }_i}{{\varvec{\upphi }} _{i,\theta }} \end{aligned}$$

(14a)

$$\begin{aligned}&{\ddot{\varvec{\upphi }} _i} = {\ddot{\psi }_i}{{\varvec{\upphi }} _{i,\psi }} + {\ddot{\theta }_i}{{\varvec{\upphi }} _{i,\theta }} + {{\dot{{\varvec{\upnu }} }}_i} \end{aligned}$$

(14b)

where ${{\dot{{\varvec{\nu }} }}_i} = \dot{\psi }_i^2{{\varvec{\upphi }} _{i,\psi \psi }} + 2{\dot{\psi }_i}{\dot{\theta }_i}{{\varvec{\upphi }} _{i,\psi \theta }} + \dot{\theta }_i^2{{\varvec{\upphi }} _{i,\theta \theta }}$, ${\varvec{\upphi }} _{i,\psi } =\left[ {{\begin{array}{c} {-s\psi _i c\theta _i } \\ {c\psi _i c\theta _i } \\ 0 \\ \end{array} }} \right]$, ${\varvec{\upphi }} _{i,\theta } =\left[ {{\begin{array}{c} {-c\psi _i s\theta _i } \\ {-s\psi _i s\theta _i } \\ {-c\theta _i } \\ \end{array} }} \right] , {\varvec{\upphi }} _{i,\psi \psi } =\left[ {{\begin{array}{c} {-c\psi _i c\theta _i } \\ {-s\psi _i c\theta _i } \\ 0 \\ \end{array} }} \right]$,    ${\varvec{\upphi }} _{i,\psi \theta } =\left[ {{\begin{array}{c} {s\psi _i s\theta _i } \\ {-c\psi _i s\theta _i } \\ 0 \\ \end{array} }} \right] , {\varvec{\upphi }} _{i,\theta \theta } =\left[ {{\begin{array}{c} {-c\psi _i c\theta _i } \\ {-s\psi _i c\theta _i } \\ {s\theta _i } \\ \end{array} }} \right] =-\,{\varvec{\upphi }} _i$.

The above relations enable us to define the following:

$$\begin{aligned}&{{{{\varvec{\upvarepsilon }} }}_{{{\mathbf{r}}_0}}} = \left[ {\begin{array}{*{20}{c}} {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{x}}_0}}} - \frac{{\partial T}}{{\partial {x_0}}}}\\ {\begin{array}{*{20}{c}} {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{y}}_0}}} - \frac{{\partial T}}{{\partial {y_0}}}}\\ {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{z}}_0}}} - \frac{{\partial T}}{{\partial {z_0}}}} \end{array}} \end{array}} \right] = {{\mathbf{M}}_{rr}}{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{rj}}{{\ddot{\mathbf{q}}}_j} + {{\mathbf{h}}_r} \nonumber \\\end{aligned}$$

(15a)

$$\begin{aligned}&{{{{\varvec{\upvarepsilon }} }}_{{{\mathbf{q}}_i}}} = \left[ {\begin{array}{*{20}{c}} {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{\psi }}_i}}} - \frac{{\partial T}}{{\partial {\psi _i}}}}\\ {\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{\dot{\theta }}_i}}} - \frac{{\partial T}}{{\partial {\theta _i}}}} \end{array}} \right] = {\mathbf{a}}_{ri}^T{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{ij}}{{\ddot{\mathbf{q}}}_j} + {{\mathbf{h}}_i}\nonumber \\ \end{aligned}$$

(15b)

where $\mathbf{M}_{rr} =\left[ {{\begin{array}{lll} m&{}\quad 0&{}\quad 0 \\ 0&{}\quad m&{}\quad 0 \\ 0&{}\quad 0&{}\quad m \\ \end{array} }} \right]$, $\mathbf{a}_{rj} ={\bar{b}}_j \mathbf{B}_j$, $\mathbf{B}_j =\left[ {{\begin{array}{ll} {{\varvec{\upphi }} _{j,\psi } }&{} {{\varvec{\upphi }} _{j,\theta } } \\ \end{array} }} \right]$, ${{\mathbf{h}}_r} = \mathop \sum \nolimits _{i = 0}^n {{\bar{b}} _i}{{{\dot{\varvec{\upnu }} }}_i}$, ${{\mathbf{a}}_{ij}} = {{\bar{d}} _{ij}}\left[ {\begin{array}{*{20}{c}} {{\varvec{\upphi }} _{i,\psi }^T{{\varvec{\upphi }} _{j,\psi }}}&{}|&{}{{\varvec{\upphi }} _{i,\psi }^T{{\varvec{\upphi }} _{j,\theta }}}\\ { - - - - }&{}|&{}{ - - - - }\\ {{\varvec{\upphi }} _{i,\theta }^T{{\varvec{\upphi }} _{j,\psi }}}&{}|&{}{{\varvec{\upphi }} _{i,\theta }^T{{\varvec{\upphi }} _{j,\theta }}} \end{array}} \right]$, ${\mathbf{{h}}_i} = \left[ {\begin{array}{*{20}{c}} {{\varvec{\upphi }} _{i,\psi }^T\mathop \sum \nolimits _{j = 0}^n {{\bar{d} }_{ij}}{{{{\dot{\varvec{\upnu }} }}}_j}}\\ { - - - - - - - - - - }\\ {{\varvec{\upphi }} _{i,\theta }^T\mathop \sum \nolimits _{j = 0}^n {{ \bar{d}}_{ij}}{{{\dot{{\varvec{\upnu }} }}}_j}} \end{array}} \right] .$

The potential energy of gravity forces of the link is defined by the following expression:

$$\begin{aligned} V_g =g\mathop \sum \limits _{i=0}^n m_i y_{Ci} \end{aligned}$$

(16)

where g is the gravity acceleration, $y_{Ci} =y_0 +\mathop \sum \nolimits _{j=0}^i b_{ij} s\psi _i c\theta _i$ are coordinates of the centre of mass of segment i.

Having used (12a), we obtain:

$$\begin{aligned}&\frac{\partial V_g }{\partial \mathbf{r}_0 }=\left[ {{\begin{array}{c} 0 \\ {mg} \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(17a)

$$\begin{aligned}&\frac{\partial V_g }{\partial \mathbf{q}_i }=\left[ {{\begin{array}{c} {c\psi _i c\theta _i } \\ {-s\psi _i s\theta _i } \\ \end{array} }} \right] {\bar{m}}_i \end{aligned}$$

(17b)

where ${\bar{m}}_i =g\mathop \sum \nolimits _{j=i}^n m_i b_{ji}$ is a constant value.

The energy of spring deformation and its derivatives can be calculated in a similar way to that presented by Wittbrodt et al. [20] and Drąg [16].

It follows from Fig. 4 that the energy of spring deformation of a link with circular cross section can be expressed as:

$$\begin{aligned} V_{s,i} =\frac{1}{2}c_i \left( {{\Delta }\alpha _i } \right) ^{2} \end{aligned}$$

(18)

where $c_i$ is the stiffness coefficient of bending, ${\Delta }\alpha _i$ is the angle between axes $x_{i-1}^{\prime }$ and $x_i^{\prime }$ dependent on $\mathbf{q}_{i-1}$ and $\mathbf{q}_i$.

Fig. 4

Angle ${\Delta }\alpha _i$, $\left\{ {x',y',z'} \right\}$—reference system with axes parallel to the local system of segment $i-1$

Angles ${\Delta }\psi _i$ and ${\Delta }\theta _i$ can be calculated in the form presented in [16].

Let

$$\begin{aligned} \mathbf{R}_{i,{\Delta }} =\mathbf{R}_{{\Delta }\psi _i } \mathbf{R}_{{\Delta }\theta _i } \end{aligned}$$

(19)

where ${\Delta }\psi _i =\psi _i -\psi _{i-1}$, ${\Delta }\theta _i =\theta _i -\theta _{i-1}$, and since due to orthonormality of matrix $\mathbf{R}_i$, the following takes place:

$$\begin{aligned} \mathbf{R}_{i, {\Delta }} =\mathbf{R}_{i-1}^T \mathbf{R}_i \end{aligned}$$

(20)

then elements of this matrix can be calculated when $\mathbf{q}_{i-1}$ and $\mathbf{q}_i$ are known. From (19), the following results are obtained:

$$\begin{aligned} \mathbf{R}_{i,{\Delta }} =\left[ {{\begin{array}{ccc} {c{\Delta }\psi _i c{\Delta }\theta _i }&{}\quad \cdots &{} \quad \cdots \\ {s{\Delta }\psi _i c{\Delta }\theta _i }&{} \quad \cdots &{} \quad \cdots \\ {-s{\Delta }\theta _i }&{}\quad \cdots &{}\quad \cdots \\ \end{array} }} \right] \end{aligned}$$

(21)

Angles ${\Delta }\psi _i$ and ${\Delta }\theta _i$ can be calculated from the relations:

$$\begin{aligned}&{\Delta }\psi _i =\hbox {arctg}\frac{\left( {\mathbf{R}_{i,{\Delta }} } \right) _{2,1} }{\left( {\mathbf{R}_{i,{\Delta }} } \right) _{1,1} } \end{aligned}$$

(22a)

$$\begin{aligned}&{\Delta }\theta _i =\hbox {arcsin}\left( {-\mathbf{R}_{i,{\Delta }} } \right) _{3,1} \end{aligned}$$

(22b)

where $\left( {\mathbf{R}_{i, {\Delta }} } \right) _{k,1}$ are elements of the first column of matrix $\mathbf{R}_{i, {\Delta }} \left( {k=1,2,3} \right)$.

Quantities ${\Delta }\alpha _i , { \Delta }\psi _i$ and ${\Delta }\theta _i$ are related in the following way:

$$\begin{aligned} \hbox {cos}\Delta \alpha _i =\hbox {cos}\Delta \psi _i \hbox {cos}\Delta \theta _i \end{aligned}$$

(23)

and thus [20]:

$$\begin{aligned} \frac{\partial V_{s,i} }{\partial \mathbf{q}_i }=c_i \frac{{\Delta }\alpha _i }{\hbox {sin}\Delta \alpha _i }\left[ {{\begin{array}{l} {\hbox {cos}\Delta \psi _i \hbox {sin}\Delta \theta _i } \\ {\hbox {sin}\Delta \psi _i \hbox {cos}\Delta \theta _i } \\ \end{array} }} \right] \end{aligned}$$

(24)

Having taken into account (15), (17) and (24), the equations of motion of the link without consideration of the influence of the sea can be presented in the form:

$$\begin{aligned}&{{\mathbf{M}}_{rr}}{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{rj}}{{\ddot{\mathbf{q}}}_j} + {{\mathbf{h}}_r} + \frac{{\partial {V_g}}}{{\partial {{\mathbf{r}}_0}}} = {{\mathbf{Q}}_r} \end{aligned}$$

(25a)

$$\begin{aligned}&{\mathbf{a}}_{ri}^T{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {\mathbf{a}}_{ij}^{}{{\ddot{\mathbf{q}}}_j} + {\mathbf{h}}_i^{} \nonumber \\&\qquad + \frac{{\partial {V_g}}}{{\partial {{\mathbf{q}}_i}}} + \frac{{\partial {V_s}}}{{\partial {{\mathbf{q}}_i}}} = {{\mathbf{Q}}_i}\quad \mathrm{for }\,\,i = 0,1,\ldots ,n \end{aligned}$$

(25b)

where $\mathbf{Q}_r$, $\mathbf{Q}_i$ are generalised forces defined in the following subsection, $\frac{\partial V_s }{\partial \mathbf{q}_i }= \frac{\partial V_{s,i} }{\partial \mathbf{q}_i }+\frac{\partial V_{s,i+1} }{\partial \mathbf{q}_i }$.

2.1 Influence of the water environment

The influence of the sea on the riser consists of the following forces:

• buoyancy forces,

• hydrodynamic forces,

• added mass forces.

Buoyancy forces acting only in the vertical direction can be calculated as:

$$\begin{aligned} \mathbf{F}_{r,i} =\left[ {{\begin{array}{lll} 0&{} \quad {F_{r,i,y} }&{}\quad 0 \\ \end{array} }} \right] ^{T} \end{aligned}$$

(26)

where $F_{r,i,y} =\varrho _w V_i g$,$V_i =A_{i,out} l_i$.

Having assumed that this force acts at the centre of mass of the segment, its coordinates are expressed as follows:

$$\begin{aligned} \mathbf{r}_{Ci} =\mathbf{r}_0 +\mathop \sum \limits _{j=0}^i b_{ij} {\varvec{\upphi }} _j \end{aligned}$$

(27)

From:

$$\begin{aligned}&\mathbf{Q}_{r,r} =\left( {\frac{\partial \mathbf{r}_{Ci} }{\partial \mathbf{r}_0 }} \right) ^{T}{} \mathbf{F}_{r,i} \end{aligned}$$

(28a)

$$\begin{aligned}&\mathbf{Q}_{r,ij} =\left[ {{\begin{array}{l} {\frac{\partial \mathbf{r}_{Ci} }{\partial \psi _j }} \\ {\frac{\partial \mathbf{r}_{Ci} }{\partial \theta _j }} \\ \end{array} }} \right] ^{T}{} \mathbf{F}_{r,i} \end{aligned}$$

(28b)

we can obtain generalised forces resulting from buoyancy forces acting on segment i in the form:

$$\begin{aligned}&\mathbf{Q}_{r,r} =\mathop \sum \limits _{j=0}^n \mathbf{F}_{r,j} \end{aligned}$$

(29a)

$$\begin{aligned}&\mathbf{Q}_{r,i} =\mathop \sum \limits _{j=i}^n \mathbf{Q}_{r,ij} =\mathbf{B}_j^T \mathop \sum \limits _{j=i}^n \mathbf{F}_{r,j} b_{ji}\,\, i=0,1,\ldots ,n\nonumber \\ \end{aligned}$$

(29b)

In order to calculate hydrodynamic damping forces, it is assumed that they can be expressed as in [26]:

$$\begin{aligned} d\mathbf{F}_{d,i}^{{\prime }} =\mathbf{S}_i^{{\prime }} d\xi \end{aligned}$$

(30)

where $\mathbf{S}_i^{\prime } =e_H \left[ {{\begin{array}{c} {D_x^{\prime } \left| {v_x^{\prime } } \right| v_x^{\prime } } \\ {D_{yz}^{\prime } \left| {v_{yz}^{\prime } } \right| v_y^{\prime } } \\ {D_{yz}^{\prime } \left| {v_{yz}^{\prime } } \right| v_z^{\prime } } \\ \end{array}}} \right] ^{T}$, $e_H =-\frac{1}{2}\varrho _w D_{i,\mathrm{out}}$, $D_{i,\mathrm{out}}$ is the external diameter of segment i of the riser, $\mathbf{{v}}^{\prime }=[v^{\prime }_x \quad v^{\prime }_y \quad v^{\prime }_z]^T$ is the relative velocity of water at point P of the riser (Fig. 2), and $v_{yz}^{\prime } =\sqrt{\left( {v_y^{\prime } } \right) ^{2}+\left( {v_z^{\prime } } \right) ^{2}}$, where $D_x^{\prime } , D_{yz}^{\prime }$ are coefficients of hydrodynamic damping.

Velocity $\mathbf{{v}}^{\prime }$ can be calculated from the formula:

$$\begin{aligned} {\mathbf{v'}} = {\mathbf{R}}_i^T\left( {{\mathbf{v}} - {{\mathbf{v}}_w}} \right) \end{aligned}$$

(31)

where ${\mathbf{v}} = {{\dot{\mathbf{r}}}_0} + \mathop \sum \nolimits _{j = 0}^{i - 1} {l_j}{\dot{\varvec{\upphi }} _j} + {\xi _i}{\dot{\varvec{\upphi }} _i}$ is the absolute velocity of point P, $\mathbf{v}_w$ is water velocity (sea current).

Force $d\mathbf{F}_{d,i}^{\prime }$ in the inertial frame of reference is expressed as:

$$\begin{aligned} d\mathbf{F}_{d,i} =\mathbf{R}_i \mathbf{S}_i^{\prime } \left( \xi \right) d\xi \end{aligned}$$

(32)

and its resulting generalised forces are:

$$\begin{aligned}&d\mathbf{Q}_{d,ir} =\left( {\frac{\partial \mathbf{r}}{\partial \mathbf{r}_0 }} \right) ^{T}d\mathbf{F}_{d,i} =\mathbf{I}_{3x3} d\mathbf{F}_{d,i} =d\mathbf{F}_{d,i} \nonumber \\\end{aligned}$$

(33a)

$$\begin{aligned}&d\mathbf{Q}_{d,ij} =\left[ {{\begin{array}{l} {\frac{\partial \mathbf{r}}{\partial \psi _j }} \\ {\frac{\partial \mathbf{r}}{\partial \theta _j }} \\ \end{array} }} \right] ^{T}d\mathbf{F}_{d,i} =\alpha _{ij} \mathbf{B}_j d\mathbf{F}_{d,i} \end{aligned}$$

(33b)

where $\mathbf{r}=\mathbf{r}_i$ defined by (2), $j=0,\ldots ,i-1$, and $\mathbf{I}_{3x3}$ is the identity matrix, $\alpha _{ij} =\left\{ {{\begin{array}{ll} l_j &{} \hbox {if }j<i \\ \xi &{} \hbox {if }j=i \\ \end{array} }} \right.$.

Forces $\mathbf{Q}_{d,ir}$ and $\mathbf{Q}_{d,ij}$ are the sum of forces $d\mathbf{Q}_{d,ir}$ and $d\mathbf{Q}_{d,ij}$:

$$\begin{aligned} \mathbf{Q}_{d,ir}= & {} \mathop \int \limits _0^{l_i } d\mathbf{Q}_{d,ir} \end{aligned}$$

(34a)

$$\begin{aligned} \mathbf{Q}_{d,ij}= & {} \mathop \int \limits _0^{l_i } d\mathbf{Q}_{d,ij} \end{aligned}$$

(34b)

If we introduce the following notation:

$$\begin{aligned}&\mathbf{S}_{i,0} =\mathbf{R}_i \mathop \int \limits _0^{l_i } \mathbf{S}_i^{\prime } \left( \xi \right) d\xi \end{aligned}$$

(35a)

$$\begin{aligned}&\mathbf{S}_{i,1} =\mathbf{R}_i \mathop \int \limits _0^{l_i } \xi \mathbf{S}_i^{\prime } \left( \xi \right) d\xi \end{aligned}$$

(35b)

then after some transformations the following is obtained:

$$\begin{aligned}&\mathbf{Q}_{d,ir} =\mathbf{S}_{i,0} \end{aligned}$$

(36a)

$$\begin{aligned}&\mathbf{Q}_{d,ij} =\mathbf{B}_j^T {{\varvec{\updelta }} }_{i,j} \end{aligned}$$

(36b)

where ${{\varvec{\updelta }} }_{i,j} =\left\{ {{\begin{array}{ll} l_j \mathbf{S}_{i,0}&{} \quad \hbox { if }j<i \\ \mathbf{S}_{i,1}&{} \quad \hbox {if }j=i \\ \end{array} }} \right.$.

Fig. 5

Constraints and their reactions at the bottom end of the riser

Table 1 Parameters of the riser used in the experiment [21]

Table 2 Influence of the number of segments n on natural frequencies for $T_U =389\hbox {N}$ exerted at the upper end of the riser

Table 3 Influence of the number of segments n on natural frequencies for $T_U =1925\hbox {N}$ exerted at the upper end of the riser

Table 4 Comparison of natural frequencies

Fig. 6

Error in the natural frequencies: calculation versus experiment

Fig. 7

Model of the riser for experimental measurements

Table 5 Characteristics of the riser model

Fig. 8

Displacements of chosen points: SM segment method, Experiment* and Simulation*—results presented in [23]

Integrals from (35) are calculated by means of Gauss formulae.

Having taken into account that:

$$\begin{aligned}&\mathbf{Q}_{d,r} =\mathop \sum \limits _{j=i}^n \mathbf{Q}_{d,jr} \end{aligned}$$

(37a)

$$\begin{aligned}&\mathbf{Q}_{d,i} =\mathop \sum \limits _{j=i}^n \mathbf{Q}_{d,ji} \end{aligned}$$

(37b)

the following formula for hydrodynamic damping forces is obtained:

$$\begin{aligned}&\mathbf{Q}_{d,r} =\mathop \sum \limits _{j=0}^n \mathbf{S}_{j,0} \end{aligned}$$

(38a)

$$\begin{aligned}&\mathbf{Q}_{d,i} =\mathop \sum \limits _{j=i}^n \mathbf{B}_j^T \mathbf{\delta }_{j,i} \end{aligned}$$

(38b)

Having taken into account (25), (29) and (38), the dynamic equilibrium equations of the riser can be written in the form:

$$\begin{aligned}&{{\mathbf{M}}_{rr}}{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{rj}}{{\ddot{\mathbf{q}}}_j} = {{\mathbf{f}}_r} + {\mathbf{F}}_0^{ext} \end{aligned}$$

(39a)

$$\begin{aligned}&{\mathbf{a}}_{ri}^T{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{ij}}{{\ddot{\mathbf{q}}}_j} = {{\mathbf{f}}_i}\quad i = 0,1, \ldots ,n \end{aligned}$$

(39b)

where $\mathbf{f}_r =-\mathbf{h}_r -\frac{\partial V_g }{\partial \mathbf{r}_0 }+\mathbf{Q}_{r,r} +\mathbf{Q}_{d,r}$, $\mathbf{f}_i =-\mathbf{h}_i -\frac{\partial V_g }{\partial \mathbf{q}_i }+\frac{\partial V_s }{\partial \mathbf{q}_i }+\mathbf{Q}_{r,i} +\mathbf{Q}_{d,\hbox {i}} , i=0,1,\ldots ,n$, $\mathbf{F}_0^{ext}$ is the vector of external forces acting at point $P_0$ (upper end of the riser).

When the motion of the upper end of the riser is known as a function of time:

$$\begin{aligned} \mathbf{r}_0 =\mathbf{r}_0 \left( t \right) \end{aligned}$$

(40)

which means that vectors ${{\dot{\mathbf{r}}}_0}\left( t \right) ,~{{\ddot{\mathbf{r}}}_0}\left( t \right)$ are also known, and Eq. (39b) can be written as follows:

$$\begin{aligned} \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{ij}}{{\ddot{\mathbf{q}}}_j} = {{\mathbf{f}}_i} - {\mathbf{a}}_{ri}^T{{\ddot{\mathbf{r}}}_0}\quad i = 0,1, \ldots ,n \end{aligned}$$

(41)

and forces causing this motion $\mathbf{F}_0^{ext}$can be calculated from (39a):

$$\begin{aligned} {\mathbf{F}}_0^{ext} = {{\mathbf{M}}_{rr}}{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{rj}}{{\ddot{\mathbf{q}}}_j} - {{\mathbf{f}}_r} \end{aligned}$$

(42)

Equations (39) or (41) form a system of $m=3+2\left( {n+1} \right)$ or $m=2\left( {n+1} \right)$ nonlinear differential equations of the second order with respect to t. The equations of motion are solved using the Runge–Kutta method with a constant integration step.

In the applications presented further in the paper, constraints are imposed on the riser, which involve placing its bottom end in a strictly defined position (Fig. 5) by means of the formula:

$$\begin{aligned} \mathbf{r}_E =\mathbf{r}_0 +\mathop \sum \limits _{j=0}^n l_j {\varvec{\upphi }} _j =\hbox {const} \end{aligned}$$

(43)

Table 6 Parameters of the riser

Fig. 9

Load on the riser a scheme of the forces acting on the riser end b course of forces $F_x$ and $F_z$

In such a case, the system considered includes additional reactions as components of vector $\mathbf{F}_E$ and constraint equations (43). Then, Eq. (39) takes the following form:

$$\begin{aligned}&{{\mathbf{M}}_{rr}}{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{rj}}{{\ddot{\mathbf{q}}}_j} - {{\mathbf{I}}_{3x3}}~{{\mathbf{F}}_E} = {{\mathbf{f}}_r} + {\mathbf{F}}_0^{ext} \end{aligned}$$

(44a)

$$\begin{aligned}&{\mathbf{a}}_{ri}^T{{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {{\mathbf{a}}_{ij}}{{\ddot{\mathbf{q}}}_j} - {{\mathbf{D}}_i}~{{\mathbf{F}}_E} = {{\mathbf{f}}_i}\quad i = 0,1, \ldots ,n\nonumber \\ \end{aligned}$$

(44b)

where $\mathbf{D}_i =-\,l_i \mathbf{B}_i^T$, and Eq. (43) can be written in the acceleration form as:

$$\begin{aligned} {{\ddot{\mathbf{r}}}_0} + \mathop \sum \limits _{j = 0}^n {l_j}{{\mathbf{B}}_j}{{\ddot{\mathbf{q}}}_j} = - \mathop \sum \limits _{j = 0}^n {l_j}{{\dot{\mathbf{v}}}_j} \end{aligned}$$

(45)

The Baumgart method is used for stabilisation of constraint equations. Initial conditions for the dynamics problem are calculated from Eqs. (39) or (41) and (43) as a solution of the static problem (${{\dot{\mathbf{r}}}_0} = {{\ddot{\mathbf{r}}}_0} = \mathbf{0};~{{\dot{\mathbf{q}}}_i} = {{\ddot{\mathbf{q}}}_i} = \mathbf{0},~i = 0,1, \ldots ,n)$. The system of nonlinear equations has been solved by means of Newton’s iterative method. Natural frequencies with and without tension at the upper end of the riser are calculated in Sect. 3.1. A procedure similar to that presented in [4, 12] is applied in order to calculate frequencies and avoid linearisation of Eqs. (39) or (41).

Fig. 10

Courses of the end of the riser in x direction a in the air, b in water

Fig. 11

Courses of the end of the riser in y direction a in the air, b in water

Fig. 12

Courses of the end of the riser in z direction a in the air, b in water

3 Validation of the model

3.1 Analysis of frequencies of free vibrations

Analysis of vortex-induced vibrations of risers is essential due to the possible fatigue damage caused by the vibrations. Thus, prediction of natural frequencies of risers is one of the crucial points in the design process of risers. The method presented enables us to calculate frequencies of free vibrations of the riser. In order to validate the model, the natural frequencies obtained using our model are compared with those from the experiment explained in [21], where Chaplin and co-authors describe experimental measurements taken on a model of a riser placed in a water tank and exposed to a stepped current. The data of the riser are presented in Table 1.

The installation of the riser consisted of universal joints at each end of the riser and a tensioning system at the upper end. Measurements of the first seven natural frequencies were taken for five different values of the top tensions.

The results of any discretisation method depend on the number of elements into which the system under consideration is divided. Thus, first the influence of the number of finite segments on the results obtained is examined for two different sets of tension applied at both ends of the riser. The results presented in Tables 2 and 3 show convergence of the results obtained for the segment method and its efficiency.

The comparative analysis is carried out not only with the experimental measurements given in [21] but also with results obtained by means of the variational iteration method (VIM) presented in [22], whose authors use the same experiment. It is assumed that the number of segments used for numerical simulations is ${{n}}={200}$. Table 4 presents comparison of the first seven natural frequencies calculated for five cases of different values of tension. The results calculated using the finite segment method are in very good agreement with both those measured in the experiment and calculated using the variational iteration method.

Figure 6 shows the relative percentage error of the simulation results compared to the measurements calculated according to the formula:

$$\begin{aligned} \varepsilon =\frac{\left| {\omega _{i,\exp } -\omega _{i,\mathrm{calc}} } \right| }{\omega _{i,\exp } }\quad 100\%\,\,i=1,\ldots ,7 \end{aligned}$$

(46)

where $\omega _{i,\exp }$, $\omega _{i,\mathrm{calc}}$ are values of the i-th natural frequency measured and calculated, respectively.

Analysis of the diagram shows that the error does not exceed 2% for most calculated values. The largest differences are obtained for the first case with the lowest tension, yet still the error is less than 6.5%, and in one case the second natural frequency is calculated with an error of about 10.5%. The distribution of errors is similar to that presented in [22], but it can be seen that in most cases the results from the finite segment method are closer to the experimental measurements than those obtained using the variational iteration method. The analysis presented generally confirms the applicability of the finite segment method for prediction of natural frequencies of rises.

3.2 Regular oscillatory vibrations

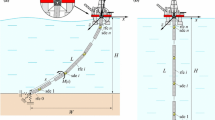
In this section, validation of the method is carried out on the basis of experiment used as a reference by many researchers [23,24,25]. A laboratory test stand consists of a long thin tube filled with water simulating a riser submerged in water with its upper end attached to a mechanism generating oscillatory motion along the x axis (Fig. 7). Additional weight W is attached at the bottom of the riser in order to keep the model straight in still water.

Cameras installed along the y axis measured x displacements at chosen points. Parameters of the riser are presented in Table 5.

Oscillatory motion exerted on the riser at point $P_0 =P$ with amplitude 0.1 m is shown in Fig. 8 as $x_P$. Numerical simulations were carried out for a riser divided into $n=20$ elements. Comparison of displacements in x direction at points A, C and E (Fig. 7) is presented in Fig. 8. The results of calculations are carried out using the finite segment method are compared with experimental measurements and simulation results presented in [23].

The comparison presented in Fig. 8 demonstrates good compatibility of the results obtained using the method presented in the paper with those from experiment and numerical simulation based on Hamilton’s principle [23].

3.2.1 Irregular forced vibrations

Validation of the model presented has also been carried out by comparing the results obtained from the authors’ own software with those from Abaqus. The comparison is concerned with forced vibrations of the riser both with and without consideration of the sea. The parameters of the riser analysed are presented in Table 6. Displacements of the free end of the riser loaded (Fig. 9a) with two forces changing in time and acting along x and z axes and with constant force $F_y=-\,30\hbox { kN}$ are analysed. Courses of forces changing in time are presented in Fig. 9b.

Calculations have been carried out using the model derived by means of the segment method (SM) dividing the riser into $n=50$ segments. First order, three-dimensional beam elements B31H have been used for discretisation in Abaqus; these elements enable longitudinal and transversal deformations to be taken into account. The same number of elements for both methods has been assumed. Displacements of the end of the riser in directions x, y, and z both without and with consideration of the sea are presented in Figs. 10, 11 and 12, respectively.

Analysis of displacement courses of the free end of the riser in interval ${<}0,100\hbox { s}{>}$ in all directions shows that results obtained by the finite segment method are compatible with those obtained using the finite element method (Abaqus). Enlargements presented in each figure show maximal and minimal displacements, and their values are presented in Table 7.

Differences between maximal and minimal displacements obtained by both methods for all directions when the riser is divided into 50 segments are listed in Table 8.

Table 7 Maximal and minimal displacements of the end of the riser along x, y, and z axes

Table 8 Absolute differences $\varepsilon _b$ for maximal and minimal values of riser displacements calculated using Abaqus and segment method for division of the riser into $n=50$ elements

Fig. 13

Projection of the trajectory of the end of the riser onto xz plane a in air, b in water

Fig. 14

Scheme of the system considered

Fig. 15

Trajectory of the upper end of the riser

The largest difference (20 cm) is related to displacements along the z axis when vibrations in air are considered; however, it has to be noted that displacements in this direction amount to $100 \hbox { m}$, which means that the relative error is 0.2%. Projections of the trajectory of the end of the riser onto plane xz are also compared, and it can be seen from Fig. 13 that the shape is similar for vibrations both without and with consideration of the sea.

It can be seen that the amplitudes when hydrodynamic damping is considered are almost an eighth of those obtained for vibrations in the air.

4 Stabilisation of the force in the connection with the wellhead

Forces occurring in the connection of a riser with a wellhead can considerably change in heavy seas and strong sea currents. Offshore equipment must be durable and reliable; therefore, it is desirable to ensure that values of these forces are as stable as possible within an accepted range despite the vertical and horizontal motion of the base (platform or vessel) .

The model proposed is numerically very effective and allows dynamic analysis for large displacements to be carried out. For example $n=25,t \in \langle 0,50\hbox {s}\rangle$, for with integration step $h=0.01\hbox {s}$, calculation time does not exceed $4\hbox { s}$. In order to illustrate the possibilities of the model, a dynamic optimisation task is formulated and solved. The problem involves selecting vertical movements of the upper end of the riser (Fig. 14) so that for a given horizontal motion of the base the forces in the connection with the wellhead are stable.

The upper end of the riser (point $P_0$) moves in the xz plane, reaching $\pm \,7\hbox { m}$ and $\pm \,3\hbox { m}$ alternately and following the trajectory presented in Fig. 15, while displacements and velocities in x and z directions change as in Fig. 16.

Two cases are considered. When simulations start, the upper end of the riser is placed at point $P_0(7\hbox { m}, 0\hbox { m}, 0\hbox { m})$, while coordinates of its bottom end are ${E}(-\,10\hbox { m},-\,499.39\hbox { m}, 0\hbox { m})$ in case A, which means that at the beginning the riser is initially slightly bent (Fig. 17a) or ${E}(-\,100\hbox { m},-\,477.16\hbox { m}, 0\hbox { m})$ in case B when the riser is initially bent (Fig. 17b).

In case B, a rotary spring with stiffness coefficient equal to $1\times 10^6\hbox { Nm}$ is placed at point $P_0$ in order to keep the deflection angle of the upper end of the riser within the limits recommended in the literature [32].

The dynamic optimisation task is formulated as minimisation of the functional:

$$\begin{aligned} {{\Omega }}\left( {{p_1}, \ldots ,{p_{m - 1}}} \right) = \sqrt{\frac{1}{T}\mathop \int \limits _0^T {{\left( {{F_E}\left( t \right) - F_E^0} \right) }^2}} \end{aligned}$$

(47)

where $p_i=y_0(t_i), i=0,\ldots ,m$ are values of the function which defines the vertical motion of the upper end of the riser at equally spaced points within time period ${<}0,T{>},F_E$ is the value of the resultant force occurring at the bottom end of the riser (E), $F_E^0$ is the initial value of the force, and T is the calculation time. Moreover, it is assumed that the minimum of functional (47) fulfils the following conditions:

$$\begin{aligned}&p_i^{\mathrm{min}} \le {p_i} \le p_i^{\mathrm{max}},\hbox { for } i = 1, \ldots ,m - 1 \end{aligned}$$

(48a)

$$\begin{aligned}&{p_0} = y\left( 0 \right) = {p_m} = y\left( T \right) = 0 \end{aligned}$$

(48b)

where $p_i^\mathrm{min}$, $p_i^\mathrm{max}$ are permissible minimal and maximal values of parameter $p_{i}$, respectively. The numerical effectiveness of the model is especially important because the solution of the dynamic optimisation problem formulated in such a way requires calculation of the functional for each combination of parameters $p_1,\ldots , p_{m-1}$, and thus integration of the equations of motion. Numerical calculations are carried out assuming $T=48\hbox { s}$, and interval is ${<} 0, T{>}$ divided into subintervals $m=12$, the first three of $1\hbox {s}$, the next seven of 3 s and last two 6 and 12 s. This means that the displacements of upper end of the riser are analysed not only during the motion of the base when $t\in {<}0,36\hbox {s}{>}$ , but also when the base is stationary for $t\in {<}36\hbox {s}, 48\,\hbox {s}{>}$. It is assumed that $m=11$ and minimal and maximal values, respectively, are equal to the following:

$$\begin{aligned} p_i^{{\mathrm{min}}} = - 2.5{\mathrm{m}}, p_i^{{\mathrm{max}}} = 0{\mathrm{m}} , \hbox {for }i = 1, \ldots ,m - 1 \end{aligned}$$

(49)

It is assumed that at the initial approximation (before optimisation) there are no vertical displacements at $P_0$ i.e. $p_i=0$ for $i=0,1,\ldots , m$. The comparison of the force courses at point (E) in the connection of the riser with the wellhead, obtained before and after solving the optimisation task, is presented in Fig. 18a. Due to the vertical motion of the upper end of the riser, the force in connection E decreases from 1150 kN to 500 kN; thus it is less than half of the initial value. Figure 18b shows force $F_0^\mathrm{ext}$ acting at the upper end of the riser and corresponding to initial approximation $y_0\equiv 0$ also before and after optimisation.

Fig. 16

a displacements in x and z directions, b velocities in x and z directions

Fig. 17

Initial position of the riser a case A, b case B

Fig. 18

Case A: course of the force before and after optimisation a at the bottom end of the riser (E), b at the upper end of the riser ($P_0$)

Fig. 19

Case A: vertical motion of the upper end of the riser a displacement, b velocity

Fig. 20

Case A: snapshots of the riser configuration at chosen moments a before, b after optimisation

Fig. 21

Case B: course of the force before and after optimisation a at the bottom end of the riser (E), b at the upper end of the riser $(P_0)$

Fig. 22

Case B: vertical motion of the upper end of the riser a displacement, b velocity

This considerable decrease in the force in connection E has been obtained as a result of applying vertical motion at the upper end of the riser in the form presented in Fig. 19.

The results presented are illustrative. Shapes of the riser at different moments of time before and after optimisation are presented in Fig. 20.

Results of calculations for case B are presented in Figs. 21 and 22.

In this case, reduction of the force acting at the bottom end of the riser (point E) is not as great as in case A. The reason is that when the riser is almost vertical (case A) forces acting at point E, when the upper end of the riser move about 14 m in x, z directions in a relatively short time, lead to a large increase in longitudinal forces. In case B, however, when the riser is significantly bent, the longitudinal forces are considerably smaller. It is important to note that as a result of the optimisation procedure for case A (slight bending of the riser) force $F_E$ is about a half of its initial value, yet still its optimal value is larger than the initial value of force $F_E$ for case B (large initial bending of the riser) .

5 Conclusions

The paper presents a different formulation of the finite segment method which uses absolute angles in contrast to the classical finite segment method, in which relative angles are used in order to describe the geometry of a slender system. Our method enables us to take into consideration the shortening of the distance between the joints, which means that the length of the slender link measured after deformation along the curvature is constant. The influence of the sea is taken into account. The method is validated by comparing the results obtained with those obtained from experimental measurements and Abaqus. The validation process shows the good correspondence of the results obtained by SM, both in natural frequencies and oscillatory vibrations, with results of measurements and calculations when different methods are applied. In addition, the comparison of results obtained with the method presented and those obtained using professional finite element method software confirms the correctness of the model and its numerical effectiveness. Even when the equations of motion are nonlinear, the integration time for less than 50 segments does not exceed 20 seconds over a time interval of 50 s with an integration step of 0.01s. Good numerical effectiveness of the method allows it to be used in solving the dynamic optimisation problem. In order to solve the optimisation problem, the equations of motion are integrated at each optimisation step (for each combination of parameters describing the objective function). In the application presented, the disturbances caused by horizontal motion of the base are neutralised by vertical motion of the upper end of the riser; this solves the problem of stabilising the force in the connection between the riser and the wellhead. The results of calculations demonstrate that even for unfavourable initial approximation of the optimisation problem (such as assuming that the upper end moves horizontally and slight initial bending) the force in the connection of the riser and wellhead is reduced considerably as a result of optimisation. Such a solution is likely to be feasible by using HCS (heave compensation system). Due to the very short calculation time, the method can be applied when teaching a neural network, which then can be used in control of the system in real time.