Skip to main content
SpringerLink
Log in

Sinusoidal control and limit cycle analysis of the dissipative Chaplygin sleigh

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

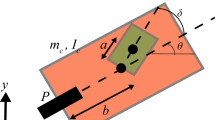
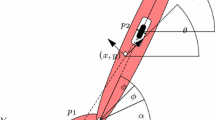
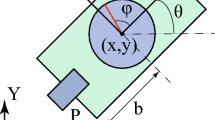
In this paper, we investigate the behavior of an underactuated mixed-dynamic nonholonomic system, a Chaplygin sleigh, subjected to viscous dissipation and sinusoidal forcing. The viscous dissipation is in the allowable directions of motion and preserves the nonholonomic constraint. The inclusion of such dissipative effects produces limit cycle oscillations in a reduced velocity space. We find analytical approximations to such limit cycles and use these to determine sinusoidal inputs to control the speed of the sleigh. We further show small changes to the sinusoidal input can steer the sleigh to any desired direction. Invariant structures like limit cycles can be expected to be seen in the dynamics of other nonholonomic systems when the effects of viscous dissipation are included. The findings we report here are therefore applicable to a broad class of both terrestrial and aquatic locomotion systems with nonholonomic constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Chaplygin, S.A.: On the theory of motion of nonholonomic systems. The theorem on the reducing multiplier. Math. Sb. 1, 303–314 (1911)

    Google Scholar 

  2. Caratheodory, C.: Der schlitten. J. Appl. Math. Mech. 13, 71–76 (1933)

    MATH  Google Scholar 

  3. Neimark, J.I., Fufaev, N.A.: Dynamics of Nonholonomic Systems. AMS, Providence (1972)

    MATH  Google Scholar 

  4. Blochm, A.M.: Nonholonomic Mechanics and Control. Springer, Berlin (2003)

    Book  Google Scholar 

  5. Chaplygin, S.A.: On the theory of motion of nonholonomic systems. The reducing-multiplier theorem. Regul. Chaotic Dyn. 13(4), 369–376 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ostrowski, J.: Computing reduced equations for robotic systems with constraints and symmetries. IEEE Trans. Robot. Autom. 15(1), 111–123 (1999)

    Article  Google Scholar 

  7. Osborne, J.M., Zenkov, D.V.: Steering the Chaplygin sleigh by a moving mass. In: Proceedings of the American Control Conference (2005)

  8. Kelly, S.D., Fairchild, M.J., Hassing, P.M., Tallapragada, P.: Proportional heading control for planar navigation: the Chaplygin beanie and fishlike robotic swimming. In: Proceedings of the American Control Conference (2012)

  9. Bizyaev, I.A., Borisov, A.V., Mamaev, I.S.: The Chaplygin sleigh with parametric excitation: chaotic dynamics and nonholonomic acceleration. Regul. Chaotic Dyn. 22(8), 955–975 (2017)

    Article  MathSciNet  Google Scholar 

  10. Bizyaev, I.A., Borisov, A.V., Kuznetsov, S.P.: Chaplygin sleigh with periodically oscillating internal mass. Europhys. Lett. 119(6), 60008 (2017)

    Article  Google Scholar 

  11. Tallapragada, P., Fedonyuk, V.: Steering a Chaplygin sleigh using periodic impulses. J. Comput. Nonlinear Dyn. 12(5), 054501 (2017)

    Article  Google Scholar 

  12. Borisov, A.V., Mamaev, I.S.: An inhomogeneous Chaplygin sleigh. Regul. Chaotic Dyn. 22(4), 435–447 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  13. Bizyaev, I.A., Borisov, A.V., Mamaev, I.S.: Dynamics of the Chaplygin sleigh on a cylinder. Regul. Chaotic Dyn. 21(1), 136–146 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Borisov, A.V., Mamaev, I.S., Bizyaev, I.A.: The Jacobi integral in nonholonomic mechanics. Regul. Chaotic Dyn. 20(3), 383–400 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Kuznetsov, S.P.: Regular and chaotic motions of the Chaplygin sleigh with periodically switched location of nonholonomic constraint. EPL (Europhys. Lett.) 118(1), 10007 (2017)

    Article  Google Scholar 

  16. Fedonyuk, V., Tallapragada, P.: The stick-slip motion of a Chaplygin sleigh witth a piecewise smooth nonholonomic constraint. In: Proceedings of the ASME DSCC (2015)

  17. Fedonyuk, V., Tallapragada, P.: Stick-slip motion of the chaplygin sleigh with a piecewise smooth nonholonomic constraint. J. Comput. Nonlinear Dyn. 12, 031021 (2017)

    Article  Google Scholar 

  18. Ostrowski, J.: Reduced equations for nonholonomic mechanical systems with dissipative forces. Rep. Math. Phys. 42(1), 185–209 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  19. Dear, T., Kelly, S.D., Travers, M., Choset, H.: Snakeboard motion planning with viscous friction and skidding. In: Proceedings of IEEE International Conference on Robotics and Automation, pp. 670–675 (2015)

  20. Borisov, A.V., Kuznetsov, S.P.: Regular and chaotic motions of a Chaplygin sleigh under periodic pulsed torque impacts. Regul. Chaotic Dyn. 21(7–8), 792–803 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Tallapragada, P.: A swimming robot with an internal rotor as a nonholonomic system. In: Proceedings of the American Control Conference (2015)

  22. Tallapragada, P., Kelly, S.D.: Integrability of velocity constraints modeling vortex shedding in ideal fluids. J. Comput. Nonlinear Dyn. 12(2), 021008 (2017)

    Article  Google Scholar 

  23. Pollard, B., Tallapragada, P.: An aquatic robot propelled by an internal rotor. IEEE/ASME Trans. Mechatron. 22(2), 931–939 (2016)

    Article  Google Scholar 

  24. Fedonyuk, V., Tallapragada, P., Wang, Y.: Limit cycle analysis and control of the dissipative Chaplygin sleigh. In: ASME Dynamic Systems and Control Conference (2017)

  25. Ijspeert, A.J.: Central pattern generators for locomotion control in animals and robots: a review. Neural Netw. 21(4), 642–653 (2008)

    Article  Google Scholar 

  26. Murray, R., Sastry, S.S.: Steering nonholonomic systems using sinusoids. In: Proceedings of the 29th Conference of Decision and Control (1990)

  27. Genesio, R., Tesi, A.: Harmonic balance methods for the analysis of chaotic dynamics in nonlinear systems. Automatica 28(3), 531–548 (1992)

    Article  MATH  Google Scholar 

  28. Basso, M., Genesio, R., Tesi, A.: A frequency method for predicting limit cycle bifurcations. Nonlinear Dyn. 13(4), 339360 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ostrowski, J.: Steering for a class of dynamic nonholonomic systems. IEEE Trans. Autom. Control 45, 14921497 (2000)

    Article  MathSciNet  Google Scholar 

  30. Bullo, F., Lewis, A.D.: Kinematic controllability and motion planning for the snakeboard. IEEE Trans. Robot. Autom. 9(3), 494–498 (2003)

    Article  Google Scholar 

  31. Chakon, O., Or, Y.: Analysis of underactuated dynamic locomotion systems using perturbation expansion: the twistcar toy example. J. Nonlinear Sci. 27, 1215–1234 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This paper is based upon work supported by the National Science Foundation under Grant Number CMMI 1563315.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Clemson University, Clemson, SC, 29631, USA

    Vitaliy Fedonyuk & Phanindra Tallapragada

Authors
  1. Vitaliy Fedonyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Phanindra Tallapragada
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vitaliy Fedonyuk.

Ethics declarations

Conflict of interest

The authors have no conflict of interest to report.

Additional information

NSF CMMI Grant 1563315.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fedonyuk, V., Tallapragada, P. Sinusoidal control and limit cycle analysis of the dissipative Chaplygin sleigh. Nonlinear Dyn 93, 835–846 (2018). https://doi.org/10.1007/s11071-018-4230-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4230-1

Keywords

Search

Navigation