Skip to main content
SpringerLink
Log in

Predicting non-stationary and stochastic activation of saddle-node bifurcation in non-smooth dynamical systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

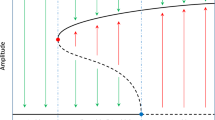
Saddle-node bifurcation can cause dynamical systems undergo large and sudden transitions in their response, which is very sensitive to stochastic and non-stationary influences that are unavoidable in practical applications. Therefore, it is essential to simultaneously consider these two factors for estimating critical system parameters that may trigger the sudden transition. Although many systems exhibit non-smooth dynamical behavior, estimating the onset of saddle-node bifurcation in them under the dual influence remains a challenge. In this work, a new theoretical framework is developed to provide an effective means for accurately predicting the probable time at which a non-smooth system undergoes saddle-node bifurcation while the governing parameters are swept in the presence of noise. The stochastic normal form of non-smooth saddle-node bifurcation is scaled to assess the influence of noise and non-stationary factors by employing a single parameter. The Fokker–Planck equation associated with the scaled normal form is then utilized to predict the distribution of the onset of bifurcations. Experimental efforts conducted using a double-well Duffing analog circuit successfully demonstrate that the theoretical framework developed in this study provides accurate prediction of the critical parameters that induce non-stationary and stochastic activation of saddle-node bifurcation in non-smooth dynamical systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Kuznetsov, Y.: Elements of Applied Bifurcation Theory, 2nd edn. Springer, New York (1998)

    MATH  Google Scholar 

  2. Kovacic, I., Brennan, M.: The Duffing Equation: Nonlinear Oscillators and Their Behaviour. Wiley, Hoboken (2011)

    Book  MATH  Google Scholar 

  3. Devoret, M., Esteve, D., Martinis, J., Cleland, A., Clarke, J.: Resonant activation of a Brownian particle out of a potential well: microwave-enhanced escape from the zero-voltage state of a Josephson junction. Phys. Rev. B 36(1), 58–73 (1987)

    Article  Google Scholar 

  4. Vijay, R., Devoret, M., Siddiqi, I.: Invited review article: the Josephson bifurcation amplifier. Rev. Sci. Instrum. 80(11), 111101 (2009)

    Article  Google Scholar 

  5. Aldridge, J., Cleland, A.: Noise-enabled precision measurements of a Duffing nanomechanical resonator. Phys. Rev. Lett. 94(15), 156403 (2005)

    Article  Google Scholar 

  6. Stambaugh, C., Chan, H.: Noise-activated switching in a driven nonlinear micromechanical oscillator. Phys. Rev. B 73(17), 172302 (2006)

    Article  Google Scholar 

  7. Harne, R.L., Wang, K.W.: Harnessing Bistable Structural Dynamics: For Vibration Control, Energy Harvesting and Sensing. Wiley, Hoboken (2017)

    Book  MATH  Google Scholar 

  8. Johnson, D.R., Thota, M., Semperlotti, F., Wang, K.W.: On achieving high and adaptable damping via a bistable oscillator. Smart Mater. Struct. 22(11), 115027 (2013)

    Article  Google Scholar 

  9. Wu, Z., Harne, R.L., Wang, K.W.: Energy harvester synthesis via coupled linear-bistable system with multi-stable dynamics. ASME J. Appl. Mech. 81(6), 061005 (2014)

    Article  Google Scholar 

  10. Harne, R.L., Wang, K.W.: A bifurcation-based coupled linear-bistable system for microscale mass sensing. J. Sound Vib. 333(8), 2241–2252 (2014)

    Article  Google Scholar 

  11. Koper, M.: Non-linear phenomena in electrochemical systems. J. Chem. Soc. Faraday Trans. 94(10), 1369–1378 (1998)

    Article  Google Scholar 

  12. Dakos, V., van Nes, E., D’Odorico, P., Scheffer, M.: Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology 93(2), 264–271 (2012)

    Article  Google Scholar 

  13. Scheffer, M., Carpenter, S., Lenton, T., Bascompte, J., Brock, W., Dakos, V., van de Koppel, J., van de Leemput, I., Levin, S., van Nes, E., Pascual, M., Vandermeer, J.: Anticipating critical transitions. Science 338(6105), 344–348 (2012)

    Article  Google Scholar 

  14. D’Souza, K., Epureanu, B., Pascual, M.: Forecasting bifurcations from large perturbation recoveries in feedback ecosystems. PLoS ONE 10(9), e0137779 (2015)

    Article  Google Scholar 

  15. Lenton, T.: Early warning of climate tipping points. Nat. Clim. Change 1(4), 201–209 (2011)

    Article  Google Scholar 

  16. Scheffer, M., Bascompte, J., Brock, W., Brovkin, V., Carpenter, S., Dakos, V., Held, H., van Nes, E., Rietkerk, M., Sugihara, G.: Early-warning signals for critical transitions. Nature 461(7260), 53–59 (2009)

    Article  Google Scholar 

  17. Hanggi, P.: Escape from a metastable state. J. Stat. Phys. 42(1–2), 105–148 (1986)

    Article  MathSciNet  Google Scholar 

  18. Meunier, C., Verga, A.: Noise and bifurcations. J. Stat. Phys. 50(1–2), 345–375 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  19. Dykman, M., Schwartz, I., Shapiro, M.: Scaling in activated escape of underdamped systems. Phys. Rev. E 72(2), 021102 (2005)

    Article  Google Scholar 

  20. Lu, C.-H., Evan-Iwanowski, R.: The nonstationary effects on a softening Duffing oscillator. Mech. Res. Commun. 21(6), 555–564 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  21. Mandel, P., Erneux, T.: The slow passage through a steady bifurcation: delay and memory effects. J. Stat. Phys. 48(5–6), 1059–1070 (1987)

    Article  MathSciNet  Google Scholar 

  22. Breban, R., Nusse, H., Ott, E.: Scaling properties of saddle-node bifurcations on fractal basin boundaries. Phys. Rev. E 68(6), 066213 (2003)

    Article  MathSciNet  Google Scholar 

  23. Berglund, N., Gentz, B.: Noise-Induced Phenomena in Slow-Fast Dynamical Systems: A Sample-Paths Approach. Springer, New York (2006)

    MATH  Google Scholar 

  24. Kuehn, C.: Multiple Time Scale Dynamics. Springer, New York (2015)

    Book  MATH  Google Scholar 

  25. Nicolis, C., Nicolis, G.: Dynamical responses to time-dependent control parameters in the presence of noise: a normal form approach. Phys. Rev. E 89(2), 022903 (2014)

    Article  Google Scholar 

  26. Miller, N., Shaw, S.: Escape statistics for parameter sweeps through bifurcations. Phys. Rev. E 85(4), 046202 (2012)

    Article  Google Scholar 

  27. Kim, J., Harne, R.L., Wang, K.W.: Predicting non-stationary and stochastic activation of saddle-node bifurcation. J. Comput. Nonlinear Dyn. 12(1), 011009 (2016)

    Article  Google Scholar 

  28. Leine, R., Van Campen, D., Keultjes, W.: Stick-slip whirl interaction in drillstring dynamics. J. Vib. Acoust. 124(2), 209–220 (2002)

    Article  Google Scholar 

  29. Sung, C., Yu, W.: Dynamics of a harmonically excited impact damper: bifurcations and chaotic motion. J. Sound Vib. 158(2), 317–329 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  30. Holmes, P., Full, R., Koditschek, D., Guckenheimer, J.: The dynamics of legged locomotion: models, analyses, and challenges. SIAM Rev. 48(2), 207–304 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  31. Iqbal, S., Zang, X., Zhu, Y., Zhao, J.: Bifurcations and chaos in passive dynamic walking: a review. Robot. Auton. Syst. 62(6), 889–909 (2014)

    Article  Google Scholar 

  32. Chua, L.: Chua’s circuit 10 years later. Int. J. Circuit Theory Appl. 22(4), 279–305 (1994)

    Article  Google Scholar 

  33. di Bernardo, M., Budd, C., Champneys, A., Kowalczyk, P., Nordmark, A., Tost, G., Piiroinen, P.: Bifurcations in nonsmooth dynamical systems. SIAM Rev. 50(4), 629–701 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Harne, R.L., Wang, K.W.: Robust sensing methodology for detecting change with bistable circuitry dynamics tailoring. Appl. Phys. Lett. 102(20), 203506 (2013)

    Article  Google Scholar 

  35. Kim, J., Harne, R.L., Wang, K.W.: Enhancing structural damage identification robustness to noise and damping with integrated bistable and adaptive piezoelectric circuitry. J. Vib. Acoust. 137(1), 011003 (2015)

    Article  Google Scholar 

  36. Zhao, X., Schaeffer, D., Berger, C., Krassowska, W., Gauthier, D.: Cardiac alternans arising from an unfolded border-collision bifurcation. J. Comput. Nonlinear Dyn. 3(4), 041004 (2008)

    Article  Google Scholar 

  37. Caballé, J., Jarque, X., Michetti, E.: Chaotic dynamics in credit constrained emerging economies. J. Econ. Dyn. Control 30(8), 1261–1275 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  38. Mosekilde, E., Laugesen, J.: Nonlinear dynamic phenomena in the Beer model. Syst. Dyn. Rev. 23(2–3), 229–252 (2007)

    Article  Google Scholar 

  39. Simpson, D.: Bifurcations in Piecewise-Smooth Continuous Systems. World Scientific, Singapore (2010)

    Book  MATH  Google Scholar 

  40. Leine, R., Nijmeijer, H.: Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Springer, New York (2013)

    MATH  Google Scholar 

  41. di Bernardo, M., Budd, C., Champneys, A., Kowalczyk, P.: Piecewise-Smooth Dynamical Systems: Theory and Applications. Springer, New York (2008)

    MATH  Google Scholar 

  42. Masri, S., Caughey, T.: On the stability of the impact damper. J. Appl. Mech. 33(3), 586–592 (1966)

    Article  MathSciNet  Google Scholar 

  43. Natsiavas, S.: Periodic response and stability of oscillators with symmetric trilinear restoring force. J. Sound Vib. 134(2), 315–331 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  44. Shaw, S., Holmes, P.: A periodically forced piecewise linear oscillator. J. Sound Vib. 90(1), 129–155 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  45. Luo, A.: The mapping dynamics of periodic motions for a three-piecewise linear system under a periodic excitation. J. Sound Vib. 283(3), 723–748 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  46. Kuehn, C.: Scaling of saddle-node bifurcations: degeneracies and rapid quantitative changes. J. Phys. A Math. Theor. 42(4), 045101 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  47. Dankowicz, H., Nordmark, A.B.: On the origin and bifurcations of stick-slip oscillations. Phys. D 136(3), 280–302 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  48. Risken, H.: The Fokker–Planck Equation. Springer, Berlin (1989)

    Book  MATH  Google Scholar 

  49. Tamaševičius, A., Mykolaitis, G., Pyragas, V., Pyragas, K.: Delayed feedback control of periodic orbits without torsion in nonautonomous chaotic systems: theory and experiment. Phys. Rev. E 76(2), 026203 (2007)

    Article  Google Scholar 

  50. Forgoston, E., Schwartz, I.: Escape rates in a stochastic environment with multiple scales. SIAM J. Appl. Dyn. Syst. 8(3), 1190–1217 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  51. Holmes, P.: A nonlinear oscillator with a strange attractor. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 292(1394), 419–448 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  52. Kovacic, I., Brennan, M.J.: The Duffing Equation: Nonlinear Oscillators and Their Behaviour. Wiley, Hoboken (2011)

    Book  MATH  Google Scholar 

  53. Rizzoni, G.: Fundamentals of Electrical Engineering. McGraw-Hill, New York (2009)

    Google Scholar 

  54. Higham, D.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This research was partially supported by the National Science Foundation under Award Nos. 1232436 and 1661568 and the University of Michigan Collegiate Professorship fund.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI, 48109, USA

    Jinki Kim & K. W. Wang

Authors
  1. Jinki Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. W. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jinki Kim.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kim, J., Wang, K.W. Predicting non-stationary and stochastic activation of saddle-node bifurcation in non-smooth dynamical systems. Nonlinear Dyn 93, 251–258 (2018). https://doi.org/10.1007/s11071-018-4189-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4189-y

Keywords

Search

Navigation