Skip to main content
SpringerLink
Log in

Topological entropy and geometric entropy and their application to the horizontal visibility graph for financial time series

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

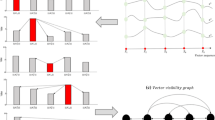
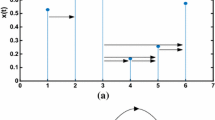
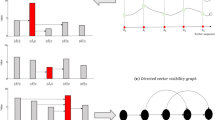
Abstract

In this paper, we introduce topological entropy (TE) based on time series, which characterizes the total exponential complexity of a quantified system with a single number. Combined with multiscale theory, we propose geometric entropy (GE), aiming to examine the correlation among different time series. In order to detect the properties of TE and GE, we apply them to an original symbolic method utilized to measure time series irreversibility, namely horizontal visibility algorithm. On this basis, we propose a time series irreversibility measure, i.e., normalized index. Then, we employ TE and GE based on the horizontal visibility graph symbolic algorithm to simulated time series, which is generated by the logistic map with different parameters. Through the comparison of the results, we find out that different simulated data have the same variation tendency of TE, which means that TE is capable of reflecting the similarity among different time series. On the basic of these results, we further analyze the irreversibility of simulated data and also get some interesting findings. From the GE results comparison, we conclude that the GE method can distinguish different time series and expose their correlation efficiently. As a farther validation, we explore the effects of these methods on the analysis of different stock time series. Results show that they can reflect a large number of interrelationships, and successfully quantify the changes in the complexity of different stock market data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Machado, J.A.T.: Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 62(1–2), 371–378 (2010)

    MathSciNet  MATH  Google Scholar 

  2. Yin, Y., Shang, P.: Weighted multiscale permutation entropy of financial time series. Nonlinear Dyn. 78(4), 2921–2939 (2014)

    Article  MathSciNet  Google Scholar 

  3. Fontaine, S., Dia, S., Renner, M.: Nonlinear friction dynamics on fibrous materials, application to the characterization of surface quality. Part I: global characterization of phase spaces. Nonlinear Dyn. 66(4), 647–665 (2011)

    Article  Google Scholar 

  4. Xiong, H., Shang, P.: Weighted multifractal cross-correlation analysis based on Shannon entropy. Commun. Nonlinear Sci. Numer. Simul. 30(1C3), 268–283 (2016)

    Article  MathSciNet  Google Scholar 

  5. Faranda, D., Pons, F.M.E., Giachino, E., Vaienti, S.: Early warnings indicators of financial crises via auto regressive moving average models. Commun. Nonlinear Sci. Numer. Simul. 29(1C3), 233–239 (2015)

    Article  MathSciNet  Google Scholar 

  6. Gabaix, X., Gopikrishnan, P., Plerou, V., Stanley, H.E.: A theory of power-law distributions in financial market fluctuations. Nature 423(6937), 267–270 (2003)

    Article  MATH  Google Scholar 

  7. Mantegna, R.N., Stanley, H.E., Chriss, N.A.: An introduction to econophysics: correlations and complexity in finance. Phys. Today 53(12), 570–571 (2000)

    Article  Google Scholar 

  8. Piqueira, J.R.C., Mortoza, L.P.D.: Brazilian exchange rate complexity: financial crisis effects. Commun. Nonlinear Sci. Numer. Simul. 17(4), 1690–1695 (2012)

    Article  Google Scholar 

  9. Machado, J.T., Duarte, F.B., Duarte, G.M.: Analysis of stock market indices through multidimensional scaling. Commun. Nonlinear Sci. Numer. Simul. 16(12), 4610–4618 (2011)

    Article  Google Scholar 

  10. Xu, M., Shang, P., Huang, J.: Modified generalized sample entropy and surrogate data analysis for stock markets. Commun. Nonlinear Sci. Numer. Simul. 35, 17–24 (2015)

    Article  MathSciNet  Google Scholar 

  11. Flanagan, R., Lacasa, L.: Irreversibility of financial time series: a graph-theoretical approach. Phys. Lett. A 380(20), 1689–1697 (2016)

    Article  Google Scholar 

  12. Forbes, K., Rigobon, R.: No contagion, only interdependence: measuring stock market comovements. J. Financ. 57(5), 2223–2261 (2002)

    Article  Google Scholar 

  13. Peter, F.J., Dimpfl, T., Huergo, L.: Using transfer entropy to measure information flows between financial markets. Stud. Nonlinear Dyn. Econom. 17(1), 85–102 (2015)

    MathSciNet  Google Scholar 

  14. Yin, Y., Shang, P.: Weighted permutation entropy based on different symbolic approaches for financial time series. Physica A 443, 137–148 (2016)

    Article  Google Scholar 

  15. Schreiber, T.: Measuring information transfer. Phys. Rev. Lett. 85(2), 461–464 (2000)

    Article  Google Scholar 

  16. Richman, J.S., Moorman, J.R.: Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278(6), H2039–H2049 (2000)

    Article  Google Scholar 

  17. Bandt, C., Pompe, B.: Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 88(17), 174102 (2002)

    Article  Google Scholar 

  18. Marschinski, R., Kantz, H.: Analysing the information flow between financial time series. Eur. Phys. J. B 30(2), 275–281 (2002)

    Article  MathSciNet  Google Scholar 

  19. Zhao, X., Shang, P., Pang, Y.: Power law and stretched exponential effects of extreme events in chinese stock markets. Fluct. Noise Lett. 09(2), 203–217 (2012)

    Article  Google Scholar 

  20. Adler, R.L., Marcus, B.: Topological Entropy and Equivalence of Dynamical Systems. American Mathematical Society, Providence (1979)

    MATH  Google Scholar 

  21. Nilsson, J.: On the entropy of a family of random substitutions. Monatshefte Fr Mathematik 168(3–4), 563–577 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  22. Denker, M., Grillenberger, C., Sigmund, K.: Topological entropy. In: Ergodic Theory on Compact Spaces. Lecture Notes in Mathematics, vol. 527, pp. 82–91. Springer, Berlin (1976)

  23. Zheleznyak, A.L.: An Approach to the Computation of the Topological Entropy. Springer, Berlin (1990)

    Book  Google Scholar 

  24. Weiss, H.: Some variational formulas for Hausdorff dimension, topological entropy, and SRB entropy for hyperbolic dynamical systems. J. Stat. Phys. 69(3), 879–886 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  25. Savkin, A.V.: Analysis and synthesis of networked control systems: topological entropy, observability, robustness and optimal control. Automatica 42, 51–62 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. Queffélec, M.: Dynamical Systems Associated with Sequences. Springer, Berlin (2010)

    Book  MATH  Google Scholar 

  27. Ghys, E., Langevin, R., Walczak, P.: Entropie geometrique des feuilletages. Acta Math. 160, 105–142 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang, S., Zhou, L., Zhou, Y.: Geometric entropy of group actions on regular curves. Adv. Math. 39(4), 467–471 (2010)

    MathSciNet  Google Scholar 

  29. Fujita, M.: Geometric entropy and hagedorn/deconfinement transition. J. High Energy Phys. 2008(9), 1–17 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Cysarz, D., Bettermann, H., Van, L.P.: Entropies of short binary sequences in heart period dynamics. Am. J. Physiol. Heart Circ. Physiol. 278(6), 183–202 (2000)

    Article  Google Scholar 

  31. Cysarz, D., Porta, A., Montano, N., Leeuwen, P.V., Kurths, J., Wessel, N.: Quantifying heart rate dynamics using different approaches of symbolic dynamics. Eur. Phys. J. Spec. Top. 222(2), 487–500 (2013)

    Article  Google Scholar 

  32. Lacasa, L., Nuñez, A., Roldán, É., Parrondo, J.M.R., Luque, B.: Time series irreversibility: a visibility graph approach. Eur. Phys. J. B 85(6), 217 (2012)

  33. Lacasa, L., Luque, B., Ballesteros, F., Luque, J., Nuño, J.C.: From time series to complex networks: the visibility graph. Proc. Natl. Acad. Sci. U. S. A. 105(13), 4972–4975 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Costa, M., Goldberger, A.L., Peng, C.K.: Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 71(2 Pt 1), 021906 (2005)

    Article  MathSciNet  Google Scholar 

  35. Xia, J., Shang, P.: Multiscale entropy analysis of financial time series. Fluct. Noise Lett. 11(11), 333–342 (2012)

    Google Scholar 

  36. Costa, M., Goldberger, A.L., Peng, C.K.: Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 92(8), 705–708 (2002)

    Google Scholar 

  37. Luque, B., Lacasa, L., Ballesteros, F., Luque, J.: Horizontal visibility graphs: exact results for random time series. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 80(2), 593–598 (2009)

    Google Scholar 

  38. Hsieh, D.A.: Chaos and nonlinear dynamics: application to financial markets. J. Financ. 46(5), 1839–1877 (1991)

    Article  Google Scholar 

  39. Guegan, D.: Chaos in economics and finance. Annu. Rev. Control 33(1), 89–93 (2009)

    Article  Google Scholar 

  40. Sauer, T., Yorke, J.A., Casdagli, M.: Embedology. J. Stat. Phys. 65(3), 579–616 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  41. Kazem, A., Sharifi, E., Hussain, F.K., Saberi, M., Hussain, O.K.: Support vector regression with chaos-based firefly algorithm for stock market price forecasting. Appl. Soft Comput. 13(2), 947–958 (2013)

    Article  Google Scholar 

  42. Masoller, C., Hong, Y., Ayad, S., Gustave, F., Barland, S., Pons, A.J., Gómez, S., Arenas, A.: Quantifying sudden changes in dynamical systems using symbolic networks. New J. Phys. 17(2), 023068 (2015)

    Article  MathSciNet  Google Scholar 

  43. Diks, C., Van Houwelingen, J., Takens, F., DeGoede, J.: Reversibility as a criterion for discriminating time series. Phys. Lett. A 201(2–3), 221–228 (1995)

    Article  Google Scholar 

  44. Cao, Y., Tung, W., Gao, J., Protopopescu, V.A., Hively, L.M.: Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 70(4), 046217 (2004)

    Article  MathSciNet  Google Scholar 

  45. Jayawardena, A., Li, W., Xu, P.: Neighbourhood selection for local modelling and prediction of hydrological time series. J. Hydrol. 258(1), 40–57 (2002)

    Article  Google Scholar 

  46. Schittenkopf, C., Dorffner, G., Dockner, E.J.: On nonlinear, stochastic dynamics in economic and financial time series. Stud. Nonlinear Dyn. Econom. 4(3), 101–121 (2000)

    Article  MATH  Google Scholar 

  47. Hong, W.C., Dong, Y., Chen, L.Y., Wei, S.Y.: SVR with hybrid chaotic genetic algorithms for tourism demand forecasting. Appl. Soft Comput. 11(2), 1881–1890 (2011)

    Article  Google Scholar 

  48. Hommes, C.H., Manzan, S.: Comments on testing for nonlinear structure and chaos in economic time series. J. Macroecon. 28(1), 169–174 (2006)

    Article  Google Scholar 

  49. Jin, L., Xin-Bao, N., Wei, W., Xiao-Fei, M.: Detecting dynamical complexity changes in time series using the base-scale entropy. Chin. Phys. 14(12), 2428 (2005)

    Article  Google Scholar 

Download references

Acknowledgements

The financial supports from the funds of the China National Science (61371130) and the Beijing National Science (4162047) are gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Science, Beijing Jiaotong University, Beijing, 100044, China

    Lei Rong & Pengjian Shang

Authors
  1. Lei Rong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pengjian Shang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lei Rong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rong, L., Shang, P. Topological entropy and geometric entropy and their application to the horizontal visibility graph for financial time series. Nonlinear Dyn 92, 41–58 (2018). https://doi.org/10.1007/s11071-018-4120-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4120-6

Keywords

Search

Navigation