Dynamical behaviour of a delayed three species predator–prey model with cooperation among the prey species

Abstract

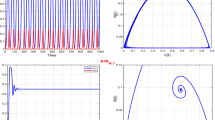
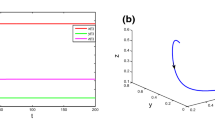
In this paper we have discussed about the dynamics of three species (two preys and one predator) delayed predator–prey model with cooperation among the preys against predation. We accept that the rate of change of density of population relies on the growth, death and in addition intra-species competition for the predators. The growth rate for preys is thought to be logistic. Delays are taken just in the growth components for each of the species. With this model we have demonstrated that the system has permanence. Taking the delays as the bifurcation parameter, the stability of the interior equilibrium point has been discussed analytically and numerically. Critical value of the delay is obtained where the Hopf-bifurcation happens. In presence of delay by constructing a Lyapunov function local asymptotic stability of the positive equilibrium point is discussed.

Appendix

$$\begin{aligned} L= & {} \frac{1}{x^*}, M=\frac{1}{y^*}, N=\frac{1}{z^*}\\ k_1= & {} \frac{1}{2l_1K_1L}+\left( c_2L+l_1c_2\tau _1\right. \\&+\,\frac{c_1c_2\tau _3+2c_2^2\tau _3+2c_2c_3\tau _3}{2} +\frac{a_1c_2\tau _1}{2}\\&+\,\frac{a_2L}{N}+\frac{l_2c_2\tau _1 K_2}{2K_1}+\frac{bc_2\tau _3}{2}+\frac{l_1c_3\tau _3}{2}\\&+\,\frac{a_2c_2\tau _3}{2L}+\frac{a_2c_2\tau _3}{2M}\\&\left. +\,\frac{2a_2c_2\tau _3}{N}+\frac{a_2c_3\tau _3}{2N}\right) \Big /\left( 2l_1L\left( -a_1N\right. \right. \\&-\,bN+\frac{a_2N}{L}+\frac{a_2N}{M}+\frac{a_1c_2\tau _3}{2}\\&+\,\frac{bc_2\tau _3}{2}+\frac{a_1c_2\tau _3}{2}+\frac{bc_3\tau _3}{2}+\frac{a_2c_2\tau _3}{2L}\\&+\,\frac{a_2c_3\tau _3}{2L}+\frac{a_2c_2\tau _3}{2M}+\frac{a_2c_3\tau _3}{2M}\\&\left. \left. +\,\frac{-2c_1N+c_1c_2\tau _3+c_1c_3\tau _3}{2}\right) \right) ,\\ k_2= & {} \frac{1}{2l_2K_2M}+\left( c_3M+l_2c_2\tau _2\right. \\&+\,\frac{c_1c_3\tau _3+2c_3^2\tau _3+2c_2c_3\tau _3}{2}+\frac{bc_3\tau _2}{2}\\&+\,\frac{a_2L}{N}+\frac{l_2c_3\tau _2 K_2}{2K_1}+\frac{bc_3\tau _3}{2}\\ \end{aligned}$$

$$\begin{aligned}&+\,\frac{l_2c_3\tau _3}{2}+\frac{a_2c_2\tau _3}{2L}+\frac{a_2c_3\tau _3}{2M}\\&\left. +\,\frac{2a_2c_3\tau _3}{N}+\frac{a_2c_3\tau _3}{2N}\right) \Big /(2l_1L(-a_1N-bN\\&+\,\frac{a_2N}{L}+\frac{a_2N}{M}+\frac{a_1c_2\tau _3}{2}+\frac{bc_2\tau _3}{2}\\&+\,\frac{a_1c_2\tau _3}{2}+\frac{bc_3\tau _3}{2}+\frac{a_2c_2\tau _3}{2L}\\&+\,\frac{a_2c_3\tau _3}{2L}+\frac{a_2c_2\tau _3}{2M}+\frac{a_2c_3\tau _3}{2M}\\&+\,\frac{-2c_1N+c_1c_2\tau _3+c_1c_3\tau _3}{2}\Bigg )\Bigg ),\\ k_3= & {} c_3N+\frac{a_2N}{M}+\frac{bc_2\tau _3}{2}+\frac{a_1c_3\tau _1}{2}\\&+\,\frac{a_2c_3\tau _2}{2}+bc_3\tau _3+\frac{bc_3\tau _2}{2}+\frac{a_2c_3\tau _1}{2M}\\&+\,\frac{a_2c_3\tau _3}{2L}+\frac{a_2c_3\tau _3}{2M}\\&+\,\frac{3a_2c_3\tau _3}{2L}+\frac{1}{2}(2c_2c_3\tau _3\\&+\,2c_3^2\tau _3\Bigg )\Big /\left( -a_1N-bN+\frac{a_2N}{L}\right. \\&+\,\frac{a_2N}{M}+\frac{a_1c_2\tau _3}{2}+\frac{bc_2\tau _3}{2}\\&+\,\frac{a_1c_2\tau _3}{2}+\frac{bc_3\tau _3}{2}+\frac{a_2c_2\tau _3}{2L}\\&+\,\frac{a_2c_3\tau _3}{2L}+\frac{a_2c_2\tau _3}{2M}+\frac{a_2c_3\tau _3}{2M}\\&+\,\frac{-2c_1N+c_1c_2\tau _3+c_1c_3\tau _3}{2}\Bigg ),\\ \end{aligned}$$

$$\begin{aligned} k_4= & {} k_5=k_6=1/\left( -a_1N-bN\right. \\&+\,\frac{a_2N}{L}+\frac{a_2N}{M}\\&+\,\frac{a_1c_2\tau _3}{2}+\frac{bc_2\tau _3}{2}+\frac{a_1c_2\tau _3}{2}\\&+\,\frac{bc_3\tau _3}{2}+\frac{a_2c_2\tau _3}{2L}+\frac{a_2c_3\tau _3}{2L}\\&+\,\frac{a_2c_2\tau _3}{2M}+\frac{a_2c_3\tau _3}{2M}\\&+\,\frac{-2c_1N+c_1c_2\tau _3+c_1c_3\tau _3}{2}\Bigg ),\\ \varLambda _1= & {} k_1\frac{l_1}{K_1}\left( -\frac{2}{x^*}+\frac{2l_1 \tau _1}{K_1}\right. \\&\left. +\,a_1 \tau _1-a_2 y^* \tau _1-a_2 z^* \tau _1\right) -k_2 \frac{l_2 a_2 z^* \tau _2}{K_2}\\&+\,k_3 \Bigg (2c_2^2\tau _3+2c_2 c_3 \tau _3-c_1 c_2 \tau _3\Bigg )+k_4\left[ \frac{c_2}{x^*}\right. \\&+\,\frac{a_2 c_2 z^*\tau _1}{2}-\frac{a_1c_2\tau _1}{2}+\frac{a_2c_2y^* \tau _1}{2}\\&-\,\frac{l_1}{K_1}\Bigg (-c_2 \tau _1+\frac{c_3 \tau _3}{2}\\&+\,\frac{c_3 \tau _1}{2}\left. -\frac{c_1 \tau _1}{2}+\frac{c_2 \tau _1}{2}\Bigg )\right] \\ \end{aligned}$$

$$\begin{aligned}&+\,k_5\left[ \frac{a_2 z^*}{x^*}+\frac{l_1 l_2}{K_1 K_2}\Bigg (\frac{\tau _2}{2}+\frac{\tau _1}{2}\Bigg )\right. \\&\left. -\,\frac{l_1}{2K_1}(2a_2 \tau _1 z^*-b\tau _1+a_2x^*\tau _1\Bigg )\right] \\&+\,k_6\left[ a_2c_2z^*\tau _3+\frac{a_2c_33z^*\tau _2}{2}-\frac{c_2l_2\tau _2}{2K_2}\right. \\&\left. +\,\frac{a_2c_2x^*\tau _3}{2}-\frac{bc_2\tau _3}{2}-\frac{l_2c_2\tau _3}{2K_2}\right] ,\\ \varLambda _2= & {} k_1\frac{-l_1 a_2z^*\tau _1}{K_1}+k_2\frac{l_2}{K_2}\left( -\frac{-2}{y^*}\right. \\&\left. +\,\frac{2l_2 \tau _2}{K_2}+b\tau _2-a_2\tau _2z^*-a_22\tau _2x^*\right) \\&+\,k_3\Bigg (2c_3^2\tau _3+2c_2c_3\tau _3-c_1c_3\tau _3\Bigg )\\&+k_4\Bigg (\frac{a_2c_2z^*\tau _1}{2}-\,\frac{c_3l_1\tau _1}{2K_1}+\frac{a_3c_3z^*\tau _3}{2}\\&+\frac{a_2c_3z^*\tau _3}{2}-\,\frac{l_1c_3\tau _3}{2K_1}+\frac{a_2c_3y^*\tau _3}{2}-\frac{a_1c_3\tau _3}{2}\Bigg )\\&+\,k_5\left[ \frac{a_2z^*}{y^*}+\frac{l_1l_2}{K_1K_2}\left( \frac{\tau _1+\tau _2}{2}\right) \right. \\&\left. -\,\frac{l_2}{2K_2}\left( a_2\tau _2 z^*-a_1\tau _2-\,a_2\tau _2y^*-a_1\tau _2z^*\right) \right] \\&+\,k_6\left[ \frac{c_3}{y^*}+\frac{a_2c_3\tau _2z^*}{2}\right. \\&+\,\frac{a_2c_3\tau _2x^*}{2}-\frac{bc_3\tau _2}{2}\\&\left. -\,\frac{l_2}{2K_2}(c_2\tau _3+4c_3\tau _2+c_2\tau _2-c_1\tau _2)\right] ,\\ \varLambda _3= & {} k_1\frac{l_1}{K_1}(a_1\tau _1-a_2y^*\tau _1)+\,k_2\frac{l_2}{K_2}(b\tau _2-a_2x^*\tau _2)\\&+\,k_3\left( -\frac{2c_1}{z^*}-c_1c_2\tau _3-c_1c_3\tau _3\right) \\&+\,k_4\Bigg (\frac{a_2y^*}{z^*}-\frac{a_1}{z^*}+\frac{c_1l_1\tau _1}{2K_1}-\,\frac{a_1c_2\tau _1}{2}\\&+\frac{a_2c_2y^*\tau _1}{2}+\,\frac{a_2c_3y^*\tau _3}{2}-\frac{a_1c_3\tau _3}{2}\Bigg )\\&+\,k_5\left[ \frac{l_1}{2K_1}(b\tau _1-a_2\tau _1x^*)\right. \\&\left. +\,\frac{l_2}{2K_2}(a_1\tau _2-a_2\tau _2y^*)\right] \\&+\,k_6\Bigg [\frac{a_2x^*-b}{z^*}+\frac{a_2c_2\tau _3x^*}{2}\\&-\,\frac{bc_2\tau _3}{2}+\frac{a_2c_3\tau _2x^*}{2}+\,\frac{c_1l_2\tau _2}{2K_2}-\frac{bc_3\tau _2}{2}\Bigg ]. \end{aligned}$$