Skip to main content
SpringerLink
Log in

Analysis of the lateral dynamics of a vehicle and driver model running straight ahead

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

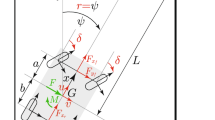
In this paper, we show that even an extremely simple nonlinear vehicle and driver model can show complex behaviors, like multi-stability and sensible dependence on the initial condition. The mechanical model of the car has two degrees of freedom, and the related equations of motion contain the nonlinear characteristics of the tires. The driver model is described by a single (nonlinear) equation, characterized by three parameters that describe how the driver steers the vehicle. Namely such parameters are the gain (steering angle per lateral deviation from desired path), the preview distance, and the reaction time delay. Bifurcation analysis is adopted to characterize straight ahead motion at different speeds, considering separately the two cases of understeering or oversteering cars. In the first case, we show that at suitable speeds the model can have three different attracting oscillating trajectories on which the system can work and that are reached due to different disturbances. In the second case, we confirm that instability arises if the forward speed is too high. The final results of the paper, bifurcation diagrams, can be used for many considerations critical both from the theoretical and from the practical viewpoints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Andrzejewski, R., Awrejcewicz, J.: Nonlinear Dynamics of a Wheeled Vehicle, vol. 10. Springer Science & Business Media, Berlin (2006)

    MATH  Google Scholar 

  2. Apel, A., Mitschke, M.: Adjusting vehicle characteristics by means of driver models. Int. J. Veh. Des. 18, 583–596 (1997)

    Google Scholar 

  3. Della Rossa, F., Mastinu, G., Piccardi, C.: Bifurcation analysis of an automobile model negotiating a curve. Veh. Syst. Dyn. 50, 1539–1562 (2012)

    Article  Google Scholar 

  4. Plochl, M., Edelmann, J.: Driver models in automobile dynamics application. Veh. Syst. Dyn. 45(7–8), 699–741 (2007)

    Article  Google Scholar 

  5. Della Rossa, F., Gobbi, M., Mastinu, G., Piccardi, C., Previati, G.: Bifurcation analysis of a car and driver model. Veh. Syst. Dyn. 52, 142–156 (2014)

    Article  Google Scholar 

  6. http://www.hytronics.at/

  7. http://www.vallelunga.it/

  8. Lozia, Z.: Modelling and simulation of a disturbance to the motion of a motor vehicle entering a skid pad as used for tests at driver improvement centres. In: Archiwum Motoryzacji vol. 69 PIMOT, Warsaw University of Technology (2015)

  9. Pacejka, H.: Tire and Vehicle Dynamics, 2nd edn. Elsevier, Amsterdam (2006)

    Google Scholar 

  10. Mastinu, G., Plöchl, M.: Road and Off-Road Vehicle System Dynamics Handbook. CRC, Boca Raton (2014)

    Google Scholar 

  11. Mitschke, M., Wallentowitz, H.: Dynamik der Kraftfahrzeuge, 4th edn. Springer, Berlin (2004)

    Book  Google Scholar 

  12. Gillespie T.D.: Fundamentals of vehicle dynamics. SAE International (1992)

  13. Abe, M.: Vehicle Handling Dynamics. Elsevier, Oxford (2015)

    Google Scholar 

  14. Jazar, R.N.: Vehicle Dynamics: Theory and Application. Springer, Berlin (2008)

    Book  Google Scholar 

  15. Andrzejewski, R., Awrejcewicz, J.: Nonlinear Dynamics of a Wheeled Vehicle. Springer, Berlin (2005)

    MATH  Google Scholar 

  16. Guiggiani, M.: The Science of Vehicle Dynamics. Springer, Berlin (2013)

    Google Scholar 

  17. Genta, G.: The Automotive Chassis. Springer, Berlin (2016)

    Google Scholar 

  18. Reimpell, J., et al.: The Automotive Chassis. Butterworth-Heineman, Oxford (2001)

    Google Scholar 

  19. Crolla, D.: Encyclopedia of Automotive Engineering. Wiley, Chichester (2015)

    Google Scholar 

  20. Dixon, J.: Tires. Suspension and Handling. Society of Automotive Engineers, Warrendale (1996)

    Google Scholar 

  21. Della Rossa, F., Sukharev, O., Mastinu, G.: Straight ahead running of a nonlinear car and driver model. In: AVEC, Munich (2016)

  22. Dhooge, A., Govaerts, W., Kuznetsov, Y.A.: MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math. Softw. 29, 141–164 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  23. Doedel, E.J., Champneys, A.R., Fairgrieve, T., et al.: AUTO-07P: continuation and bifurcation software for ordinary differential equations. Concordia University, Montreal (2007)

  24. Kuznetsov, YuA: Elements of Applied Bifurcation Theory. Springer, New York (2004)

  25. Mastinu, G., Della Rossa, F., Piccardi, C.: Nonlinear dynamics of a road vehicle running into a curve. Appl. Chaos Nonlinear Dyn. Sci. Eng. 2, 125–153 (2012)

    MathSciNet  Google Scholar 

  26. Pacejka, H.: Simplified analysis of steady-state turning. Veh. Syst. Dyn. 21, 269–296 (1973)

    Google Scholar 

  27. Gobbi, M., Mastinu, G., Previati, G., De Filippi, R., Lunetta, I., Moscatelli, D.: Optimal design of an electric power steering system for sport cars. In: 23rd International Symposium on Dynamics of Vehicles on Roads and Tracks, 19–23 Aug Qingdao, China (2013)

  28. True, H.: Multiple attractors and critical parameters and how to find them numerically: the right, the wrong and the gambling way. Veh. Syst. Dyn. 51(3), 443–459 (2013)

    Article  Google Scholar 

  29. Liu, Z., Payre, G., Bourassa, P.: Stability and oscillations in a time-delayed vehicle system with driver control. Nonlinear Dyn. 35, 159–173 (2004)

    Article  MATH  Google Scholar 

  30. Liu, Z., Payre, G., Bourassa, P.: Nonlinear oscillations and chaotic motions in a road vehicle system with driver steering control. Nonlinear Dyn. 9, 281–304 (1996)

    Article  Google Scholar 

  31. Tang, T., Li, C., Huang, H., Shang, H.: A new fundamental diagram theory with the individual difference of the driver’s perception ability. Nonlinear Dyn. 67, 2255–2265 (2012)

    Article  Google Scholar 

  32. Yi-Rong, K., Di-Hua, S., Shu-Hong, Y.: A new car-following model considering driver’s individual anticipation behavior. Nonlinear Dyn. 82, 1293–1302 (2015)

    Article  MathSciNet  Google Scholar 

  33. Wen, H., Rong, Y., Zeng, C., Qi, W.: The effect of driver’s characteristics on the stability of traffic flow under honk environment. Nonlinear Dyn. 84, 1517–1528 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Politecnico di Milano, Piazza Leonardo da Vinci 32, Milan, Italy

    Fabio Della Rossa & Gianpiero Mastinu

Authors
  1. Fabio Della Rossa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gianpiero Mastinu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fabio Della Rossa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Della Rossa, F., Mastinu, G. Analysis of the lateral dynamics of a vehicle and driver model running straight ahead. Nonlinear Dyn 92, 97–106 (2018). https://doi.org/10.1007/s11071-017-3478-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3478-1

Keywords

Search

Navigation