Dark spatiotemporal optical solitary waves in self-defocusing nonlinear media

Abstract

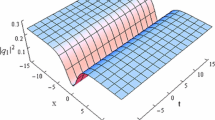
Dark three-dimensional spatiotemporal solitons or the “dark light bullets” in the self-defocusing nonlinear media with equal diffraction and dispersion lengths are demonstrated analytically. Our results show that the main characteristic of the dark light bullets can be described by the cylindrical Korteweg–de Vries (CKdV) equation. The dark wave packets are composed of the single-layer and multilayer toroidal rings. For the multilayer rings, there exist small inner rings enclosed in a large ring-shaped toroidal structure, when one chooses different orders of the soliton solutions of the CKdV equation. The radius of dark ring solitons increases with the propagation distance. Present results provide a feasible method for controlling the fundamental structure of these beams in the self-defocusing nonlinear media.

Appendix

In this Appendix, we show how to obtain multiple soliton solutions of the KdV Eq. (7), represented in the Hirota’s bilinear form. The details can be find in any good introductory account of the Hirota bilinear method, such as  [28]. To this end, we make use of the following logarithmic transformation: $w\left( {\zeta , T} \right) \,{=}\,-2\frac{\partial ^{2}\ln f\left( {\zeta ,T} \right) }{\partial T^{2}}$. Substituting it into Eq. (7), we obtain a bilinear form of the KdV equation for f, as:

(9)

As usual, the Hirota bilinear operator is defined as

$$\begin{aligned}&D_\zeta ^m D_T^n \left( {f\cdot g} \right) =\left( {\partial _\zeta -\partial _{{\zeta }'} } \right) ^{m}\left( {\partial _T -\partial _{{T}^{\prime }} } \right) ^{n}\nonumber \\&\quad \times f\left( {\zeta ,T} \right) \left. {g\left( {{\zeta }^{\prime },{T}^{\prime }} \right) } \right| _{\zeta ={\zeta }^{\prime },T={T}^{\prime }}. \end{aligned}$$

(10)

Special solutions for f can be obtained by expanding it perturbatively as $f\,{=}\,1+\lambda f_1 +\lambda ^{2}f_2 +\lambda ^{3}f_3+\cdots$, where $\lambda$ is supposed to be small. Plugging this ansatz into Eq. (9) and collecting terms pertaining to the same powers of $\lambda$, we obtain a system of linear partial differential equations. From the expansion terms $f_{1,} f_{2,} f_{3,{\ldots }}$ one forms the Nth-order solitary wave solutions of Eq. (7).

1.1 One-soliton solution

It is easily checked that if $f_1 \,{=}\,\hbox {e}^{\Omega _1 }$ with $\Omega _1\,{=}\,k_1 T-k_1^3 \zeta +\theta _{10}$, then $f_{2} \,{=}\,f_3 \,{=}\,\cdots \,{=}\,0$. Letting $\lambda \,{=}\,1$, we obtain the one-soliton solution of Eq. (7),

$$\begin{aligned} w_1 \left( {\zeta ,T} \right)= & {} -\frac{2k_1^2\text{ e }^{k_1 T-k_1^3 \zeta +\theta _{10} }}{\left( {1+\text{ e }^{k_1 T-k_1^3 \zeta +\theta _{10} }} \right) ^{2}}\nonumber \\= & {} -\frac{k_1^2 }{2}\hbox {sech}^{{2}}\left[ {\frac{k_1 T-k_1^3 \zeta +\theta _{10} }{2}} \right] , \end{aligned}$$

(11)

where $k_1$ and $\theta _{10}$ are the KdV soliton amplitude and the initial phase shift, respectively.

1.2 Two-soliton solution

Equation (9) is a linear equation, for which the superposition principle holds, so we may add a number of exponential terms to $f_2$; let us suppose that $f_1 \,{=}\,\text{ e }^{\Omega _1 }+\text{ e }^{\Omega _2 }, f_2 \,{=}\,\hbox {e}^{\Omega _1 +\Omega _2 +\Lambda _{{12}} }$, where $\Omega _j \,{=}\,k_j T-k_j^3 \zeta +\theta _{j0}\ (j=1,2)$ and $\text{ e }^{\Lambda _{12} }=\left( {\frac{k_1 -k_2 }{k_1 +k_2 }} \right) ^{2}$. Thus, letting $\lambda \,{=}\,1$, we obtain the two-soliton solution of Eq. (7),

$$\begin{aligned} w_{2} \left( {\zeta ,T} \right) =-2\frac{\partial ^{2}}{\partial T^{2}}\ln \left( \hbox {1}+\text{ e }^{\Omega _1 }+\text{ e }^{\Omega _2 }+\text{ e }^{\Omega _1 +\Omega _2 +\Lambda _{{12}} } \right) .\nonumber \\ \end{aligned}$$

(12)

1.3 Three-soliton solution

When $j\,{=}\,3$, the calculation of this case is a tedious but straightforward algebraic exercise. For $f_j\ (j\,{=}\,1,2,3)$, we choose: $f_1 \,{=}\,\text{ e }^{\Omega _1 }+\text{ e }^{\Omega _2 }+\text{ e }^{\Omega _3 },f_2 \,{=}\,\text{ e }^{\Omega _1 +\Omega _2 +\Lambda _{{12}} }+\text{ e }^{\Omega _1 +\Omega _3 +\Lambda _{{13}} }+\text{ e }^{\Omega _2 +\Omega _3 +\Lambda _{{23}} }, f_3 \,{=}\,\text{ e }^{\Omega _1 +\Omega _2 +\Omega _3 +\Lambda _{{12}} +\Lambda _{{13}} +\Lambda _{{23}} }$, where $\Omega _j \,{=}\,k_j T-k_j^3 \zeta +\theta _{j0}$, in which each term describes a one-soliton. A long calculation then leads to the similar expression of the three-soliton solution of Eq. (7):

$$\begin{aligned}&w_{3} \left( {\zeta ,T} \right) =-2\frac{\partial ^{2}}{\partial T^{2}}\ln \left( \hbox {1}+\text{ e }^{\Omega _1 }\right. \nonumber \\&\quad \left. +\,\text{ e }^{\Omega _2 }+\text{ e }^{\Omega _3 }+\text{ e }^{\Omega _1 +\Omega _2 +\Lambda _{{12}} }+\text{ e }^{\Omega _1 +\Omega _3 +\Lambda _{{13}} }\right. \nonumber \\&\quad \left. +\,\text{ e }^{\Omega _2 +\Omega _3 +\Lambda _{{23}} }+\text{ e }^{\Omega _1 +\Omega _2 +\Omega _3 +\Lambda _{{12}} +\Lambda _{{13}} +\Lambda _{{23}} } \right) , \end{aligned}$$

(13)

with $\text{ e }^{\Lambda _{jl} }=\left( {\frac{k_j -k_l }{k_j +k_l }} \right) ^{2}$, where $j<l$, $j,l=1,2,3$.

1.4 The Nth-soliton solution

More generally, one can write the Nth-order solitary wave solution of Eq. (7) in the form:

$$\begin{aligned}&w_N \left( {\zeta ,T} \right) \nonumber \\&\quad =-2\frac{\partial ^{2}}{\partial T^{2}}\ln \left[ \sum _{\mu =0,1} \exp \left( \sum _{j=0}^N \mu _j \left( {k_j T{-}k_j^3 \zeta {+}\theta _{j0} } \right) \right. \right. \nonumber \\&\quad \left. \left. \quad +\,\sum _{1\le j<l}^N {\mu _j \mu _l \Lambda _{jl} } \right) \right] , \end{aligned}$$

(14)

where $\exp \Lambda _{ij} \,{=}\,\frac{\left( {k_i -k_j } \right) ^{2}}{\left( {k_i +k_j } \right) ^{2}}$. The sum $\sum _{\mu =0,1}$ involves all possible combinations of $\mu _1 \,{=}\,0,1$; $\mu _2 \,{=}\,0,1$...; $\mu _N \,{=}\,0,1$. It indicates that there are $\hbox {2}^{N}$ terms. When all $\mu _j$ are zero, the corresponding term is 1, while when $\mu _{1} \,{=}\,\hbox {0}$ and other $\mu _j \,{=}\,\hbox {1}$, the corresponding term is $\exp \left( {\sum \nolimits _{j=2}^N {\left( {k_j T-k_j^3 \zeta +\theta _{j0} } \right) +\sum \nolimits _{2\le j<l}^N {\Lambda _{jl} } } } \right)$.