Skip to main content
SpringerLink
Log in

The Melnikov method of heteroclinic orbits for a class of planar hybrid piecewise-smooth systems and application

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

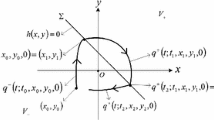
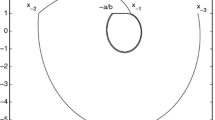
In this work, we extend the well-known Melnikov method for smooth systems to a class of planar hybrid piecewise-smooth systems, defined in three zones separated by two switching manifolds \(x=-\alpha \) and \(x=\beta \). We suppose that the dynamic in each zone is governed by a smooth system. When a trajectory reaches the switching manifolds, then reset maps describing impacting rules on the switching manifolds will be applied instantaneously before the trajectory enters into the other zone. We also assume that the unperturbed system is a piecewise-defined continuous Hamiltonian system and possesses a pair of heteroclinic orbits transversally crossing the switching manifolds. Then, we study the persistence of the heteroclinic orbits under a non-autonomous periodic perturbation and the reset maps. In order to obtain this objective, we derive a Melnikov-type function by using the Hamiltonian function to measure the distance of the perturbed stable and unstable manifolds in this system. Finally, we employ the obtained Melnikov-type function to study the persistence of a heteroclinic cycle and complicated dynamics near the heteroclinic cycle for a concrete planar piecewise-smooth system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Brogliato, B.: Nonsmooth Mechanics. Springer, London (1999)

    Book  MATH  Google Scholar 

  2. Bernardo, M.D., Kowalczyk, P., Nordmark, A.B.: Sliding bifurcations: a novel mechanism for the sudden onset of chaos in dry friction oscillators. Int. J. Bifurc. Chaos Appl. Sci. Eng. 13, 2935–2948 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  3. Banerjee, S., Verghese, G.: Nonlinear Phenomena in Power Electronics: Attractors, Bifurcations. Chaos and Nonlinear Control. Wiley-IEEE Press, New York (2001)

    Book  Google Scholar 

  4. Garcia, M., Chatterjee, A., Ruina, A., Coleman, M.: The simplest walking model:stability, complexity and scaling ASME. J. Biomech. Eng. 120, 281–288 (1998)

    Article  Google Scholar 

  5. Bernardo, M.D., Garofalo, L., Vasca, F.: Bifurcations in piecewise-smooth feedback systems. Int. J. Control 75, 1243–1259 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kunze, M.: Non-smooth Dynamical Systems. Springer, Berlin (2000)

    Book  MATH  Google Scholar 

  7. Awrejcewicz, J., Holicke, M.M.: Smooth and Nonsmooth High Dimensional Chaos and Melnikov-Type Method. World Scientific, Singapore (2007)

    MATH  Google Scholar 

  8. Bernardo, M.D., Budd, C.J., Champneys, A.R., Kowalczyk, P.: Piecewise-Smooth Dynamical Systems: Theory and Application. Springer, London (2008)

    MATH  Google Scholar 

  9. Leine, R.I., Van Campen, D.H., Van de Vrande, B.L.: Bifurcations in nonlinear discontinuous systems. Nonlinear Dyn. 23, 105–164 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  10. Makarenkov, O., Lamb, J.S.W.: Dynamics and bifurcations of nonsmooth systems: a survey. Phys. D 241, 1826–1844 (2012)

    Article  MathSciNet  Google Scholar 

  11. Melnikov, V.K.: On the stability of the center for time periodic perturbations. Tans. Moscow Math. Soc. 12, 1–57 (1963)

    MathSciNet  Google Scholar 

  12. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical System and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

  13. Wiggins, S.: Global Bifurcations and Chaos-Analytical Methods. Springer, New York (1988)

    Book  MATH  Google Scholar 

  14. Kukučka, P.: Melnikov method for discontinuous planar systems. Nonlinear Anal. 66, 2698–2719 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Battelli, F., Fečkan, M.: Homoclinic trajectories in discontinuous systems. J. Dyn. Differ. Equ. 20, 337–376 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Battelli, F., Fečkan, M.: Bifurcation and chaos near sliding homoclinics. J. Differ. Equ. 248, 2227–2262 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  17. Battelli, F., Fečkan, M.: Nonsmooth homoclinic orbits, Melnikov functions and chaos in discontinuous systems. Phys. D 241, 1962–1975 (2012)

    Article  MathSciNet  Google Scholar 

  18. Li, S.B., Zhang, W., Hao, Y.X.: Melnikov-type method for a class of discontinuous planar systems and applications. Int. J. Bifurc. Chaos 24(1450022), 1–18 (2014)

    MathSciNet  Google Scholar 

  19. Du, Z., Zhang, W.: Melnikov method for homoclinic bifurcations in nonlinear impact oscillators. Comput. Math. Appl. 50, 445–458 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  20. Granados, A., Hogan, S.J., Seara, T.M.: The Melnikov method and subharmonic orbits in a piecewise-smooth system. SIAM J. Appl. Dyn. Syst. 11, 801–830 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Carmona, V., Fernández-García, S., Freire, E., Torres, F.: Melnikov theory for a class of planar hybrid systems. Phys. D 248, 44–54 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Granados, A., Hogan, S.J., Seara, T.M.: The scattering map in two coupled piecewise-smooth systems, with numerical application to rocking blocks. Phys. D 269, 1–20 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li, S.B., Shen, C., Zhang, W., Hao, Y.X.: Homoclinic bifurcations and chaotic dynamics for a piecewise linear system under a periodic excitation and a viscous damping. Nonlinear Dyn. 79, 2395–2406 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Gao, J., Du, Z.: Homoclinic bifurcation in a quasiperiodically excited impact inverted pendulum. Nonlinear Dyn. 79, 445–458 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Castro, J., Alvarez, J.: Melnikov-type chaos of planar systems with two discontinuities. Int. J. Bifurc. Chaos 25, 1550027 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Tian, R.L., Zhou, Y.F., Zhang, B.L., Yang, X.W.: Chaotic threshold for a class of impulsive differential system. Nonlinear Dyn. 79, 445–458 (2015)

  27. Li, S.B., Ma, W.S., Zhang, W., Hao, Y.X.: Melnikov method for a three-zonal planar hybrid piecewise-smooth system and application. Int. J. Bifurc. Chaos 26(1650014), 1–13 (2016)

    MathSciNet  MATH  Google Scholar 

  28. Li, S.B., Ma, W.S., Zhang, W., Hao, Y.X.: Melnikov method for a class of planar hybrid piecewise-smooth systems. Int. J. Bifurc. Chaos 26(1650030), 1–12 (2016)

    MathSciNet  MATH  Google Scholar 

  29. Bertozzi, A.L.: Heteroclinic orbits and chaotic dynamics in planar fluid flow. SIAM J. Math. Anal. 19, 1271–1294 (1988)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the support of the National Natural Science Foundation of China (NNSFC) through Grant Nos. 11472298, 11290152, 11427801, 11272063, 11472056, the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB), the Natural Science Foundation of Tianjin City through Grant No. 13JCQNJC04400 and the Fundamental Research Funds for the Central Universities through Grant No. 3122013k005.

Author information

Authors and Affiliations

  1. College of Science, Civil Aviation University of China, Tianjin, 300300, China

    Shuangbao Li & Chao Shen

  2. Beijing Key Laboratory on Nonlinear Vibrations and Strength of Mechanical Structures, College of Mechanical Engineering, Beijing University of Technology, Beijing, 100022, China

    Wei Zhang

  3. College of Mechanical Engineering, Beijing Information Science and Technology University, Beijing, 100192, China

    Yuxin Hao

Authors
  1. Shuangbao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chao Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yuxin Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuangbao Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, S., Shen, C., Zhang, W. et al. The Melnikov method of heteroclinic orbits for a class of planar hybrid piecewise-smooth systems and application. Nonlinear Dyn 85, 1091–1104 (2016). https://doi.org/10.1007/s11071-016-2746-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2746-9

Keywords

Search

Navigation