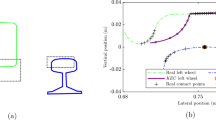Skip to main content
SpringerLink
Log in

A frictional contact finite element for wheel/rail dynamic simulations

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

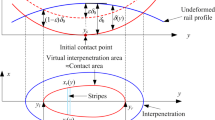
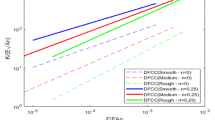
The main purpose of this paper is to develop a simple-model moving wheel/rail contact element, so that the sticking, sliding, and separation modes of the wheel/rail contact can be appropriately simulated. In the proposed finite element, the wheel and rail are simulated using the cubic-spline contact element, and a power function normal stiffness and a constant horizontal stiffness are connected to the cubic-spline contact stiffness. The three-dimensional (3D) contact finite element analysis for a realistic wheel and rail was used to accurately model the wheel/rail contact stiffness. The validated examples show that the proposed nonlinear moving wheel element can simulate the complicated sliding, sticking, and separation contact problems with good accuracy. The complicated contact modes, including the multiple contact situation between wheel flange and rail side, can also be simulated accurately. Moreover, the computer memory and CPU time required to achieve this are much less than needed with the 3D finite element contact model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Lin, Y.H., Trethewey, M.W.: Finite element analysis of elastic beams subjected to moving dynamic loads. J. Sound Vib. 136(2), 323–342 (1990)

    Article  Google Scholar 

  2. Fryba, L.: Vibration of Solids and Structures Under Moving Load. Thomas Telford, London (1999)

    Book  MATH  Google Scholar 

  3. Bowe, C.J., Mullarkey, T.P.: Wheel–rail contact elements incorporating irregularities. Adv. Eng. Softw. 36(11–12), 827–837 (2005)

    Article  Google Scholar 

  4. Sun, Y.Q., Dhanasekar, M., Roach, D.: A three-dimensional model for the lateral and vertical dynamics of wagon-track systems. Proc. Inst. Mech. Eng., Part F J. Rail Rapid Transit 217(1), 31–45 (2003)

    Article  Google Scholar 

  5. Ju, S.H., Lin, H.D., Hsueh, C.C., Wang, S.L.: A simple finite element model for vibration analyses induced by moving vehicles. Int. J. Numer. Method Eng. 68(12), 1232–1256 (2006)

    Article  MATH  Google Scholar 

  6. Xiao, X.B., Wen, Z.F., Jin, X.S., Sheg, X.Z.: Effects of track support failures on dynamic response of high speed tracks. Int. J. Nonlinear Sci. Numer. Simul. 8(4), 615–630 (2007)

    Article  Google Scholar 

  7. Rathod, C., Shabana, A.A.: Geometry and differentiability requirements in multibody railroad vehicle dynamic formulations. Nonlinear Dyn. 47(1–3), 249–261 (2007)

    MATH  Google Scholar 

  8. Dinh, V.N., Kim, K.D., Warnitchai, P.: Simulation procedure for vehicle–substructure dynamic interactions and wheel movements using linearized wheel–rail interfaces. Finite Elem. Anal. Des. 45(5), 341–356 (2009)

    Article  Google Scholar 

  9. Recuero, A.M., Escalona, J.L., Shabana, A.A.: Finite-element analysis of unsupported sleepers using three-dimensional wheel–rail contact formulation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 225(2), 153–165 (2011)

    Google Scholar 

  10. Yang, Y.B., Lin, B.H.: Vehicle–bridge interaction analysis by dynamic condensation method. J. Struct. Eng.-ASCE 121(11), 1636–1643 (1995)

    Article  Google Scholar 

  11. Au, F.T.K., Wang, J.J., Cheung, Y.K.: Impact study of cable-stayed railway bridges with random rail irregularities. Eng. Struct. 24(5), 529–541 (2002)

    Article  Google Scholar 

  12. Kwark, J.W., Choi, E.S., Kim, Y.J., Kim, B.S., Kim, S.I.: Dynamic behavior of two-span continuous concrete bridges under moving high-speed train. Comput. Struct. 82(4–5), 463–474 (2004)

    Article  Google Scholar 

  13. Xia, H., Zhang, N.: Dynamic analysis of railway bridge under high-speed train. Comput. Struct. 83(23–24), 1891–1901 (2005)

    Article  Google Scholar 

  14. Xia, H., Han, Y., Zhang, N., Guo, W.W.: Dynamic analysis of train–bridge system subjected to non-uniform seismic excitations. Earthq. Eng. Struct. Dyn. 35(12), 1563–1579 (2006)

  15. Auersch, L.: The excitation of ground vibration by rail traffic: theory of vehicle–track–soil interaction and measurements on high-speed lines. J. Sound Vib. 284(1–2), 103–132 (2005)

    Article  Google Scholar 

  16. Xi, S., Andreas, P.A.: Measurement and modeling of normal contact stiffness and contact damping at the meso scale. Trans. ASME 127(1), 52–60 (2005)

    Article  Google Scholar 

  17. Lei, X., Zhang, B.: Analyses of dynamic behavior of track transition with finite elements. J. Vib. Control 17(11), 1733–1747 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Gupta, S., Degrande, G., Lombaert, G.: Experimental validation of a numerical model for subway induced vibrations. J. Sound Vib. 321(3–5), 786–812 (2009)

    Article  Google Scholar 

  19. Connolly, D., Giannopoulos, A., Forde, M.C.: Numerical modelling of ground borne vibrations from high speed rail lines on embankments. Soil Dyn. Earthq. Eng. 46, 13–19 (2013)

    Article  Google Scholar 

  20. Seo, J.H., Sugiyama, H., Shabana, A.: Three-dimensional large deformation analysis of the multibody pantograph/catenary systems. Nonlinear Dyn. 42(2), 199–215 (2005)

    Article  MATH  Google Scholar 

  21. Tanabe, M., Matsumoto, N., Waku, H., Sogabe, M., Okuda, H.: A simple and efficient numerical method for dynamic interaction analysis of a high-speed train and railway structure during an earthquake. J. Comput. Nonlinear Dyn. 3(4), Article Number 041002 (2008)

  22. Dinh, V.N., Kima, K.D., Warnitchai, P.: Dynamic analysis of three-dimensional bridge–high-speed train interactions using a wheel–rail contact model. Eng. Struct. 31(12), 3090–3106 (2009)

    Article  Google Scholar 

  23. Nishimura, K., Terumichi, Y., Morimura, T., Sogabe, K.: Development of vehicle dynamics simulation for safety analyses of rail vehicles on excited tracks. J. Comput. Nonlinear Dyn. 4(1), Article Number 011001 (2009)

  24. Li, Q., Xu, Y.L., Wu, D.J., Chen, Z.W.: Computer-aided nonlinear vehicle–bridge interaction analysis. J. Vib. Control 16(12), 1791–1816 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ju, S.H.: A simple finite element for nonlinear wheel/rail contact and separation simulations. J. Vib. Control 20(3), 330–338 (2014)

    Article  Google Scholar 

  26. Pombo, J., Ambrosio, J.: An alternative method to include track irregularities in railway vehicle dynamic analyses. Nonlinear Dyn. 68(1–2), 161–176 (2012)

    Article  Google Scholar 

  27. Antolin, P., Zhang, N., Goicolea, J.M., Xia, H., Astiz, M., Oliva, J.: Consideration of nonlinear wheel–rail contact forces for dynamic vehicle–bridge interaction in high-speed railways. J. Sound Vib. 332(5), 1231–1251 (2013)

    Article  Google Scholar 

  28. Kouroussis, G., Verlinden, O.: Prediction of railway ground vibrations: accuracy of a coupled lumped mass model for representing the track/soil interaction. Soil Dyn. Earthq. Eng. 69, 220–226 (2015)

    Article  Google Scholar 

  29. Montenegro, P.A., Neves, S.G.M., Calcada, R.: Wheel–rail contact formulation for analyzing the lateral train–structure dynamic interaction. Comput. Struct. 152, 200–214 (2015)

    Article  Google Scholar 

  30. Ju, S.H.: A cubic–spline contact element for frictional contact problems. J. Chin. Inst. Eng. 21(2), 119–128 (1998)

    Article  Google Scholar 

Download references

Acknowledgments

This study was supported by the National Science Council, Republic of China, under contract number: NSC97-2221-E-006-116-MY3.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, National Cheng-Kung University, Tainan City, Taiwan, ROC

    S. H. Ju

Authors
  1. S. H. Ju
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. H. Ju.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ju, S.H. A frictional contact finite element for wheel/rail dynamic simulations. Nonlinear Dyn 85, 365–374 (2016). https://doi.org/10.1007/s11071-016-2691-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2691-7

Keywords

Search

Navigation