Skip to main content

Advertisement

SpringerLink
Log in

Vibration energy harvesting with a nonlinear structure

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

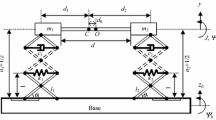
In the paper, beneficial nonlinearities incurred by an X-shape structure are explored for advantageous vibration energy harvesting performance. To this aim, a nonlinear structure beneficial for vibration energy harvesting is proposed, which is composed by X-shape supporting structures and a rigid body. By designing structure nonlinearities, which are determined by several key structure parameters, the power output peak of the harvesting system can be much improved and the effective frequency bandwidth for energy harvesting can be obviously increased, especially at the low frequency range. A coupling effect can be created among nonlinear stiffness and damping characteristics by constructing a 2-DOF vibration system, which has great influence on the energy harvesting performance. The proposed nonlinear energy harvesting systems can obviously outperform the corresponding linear systems in the whole frequency range and also demonstrate advantages compared with some other existing nonlinear energy harvesting systems in the literature. The results in this study provide a novel and practical method for the design of effective and efficient energy harvesting systems (especially in the low frequency range).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Tang, L.H., Yang, Y.W., Soh, C.K.: Toward broadband vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 21, 1867–1898 (2010)

    Article  Google Scholar 

  2. Chen, Z.S., Guo, B., Yang, Y.M., Cheng, C.C.: Metamaterials-based enhanced energy harvesting: a review. Phys. B 438, 1–8 (2014)

    Article  Google Scholar 

  3. Twiefel, J., Westermann, H.: Survey on broadband techniques for vibration energy harvesting. J. Intell. Mater. Syst. Struct. 24, 1291–1302 (2013)

    Article  Google Scholar 

  4. Harne, R.L., Wang, K.W.: A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22, 023001 (2013)

    Article  Google Scholar 

  5. Stephen, N.G.: On energy harvesting from ambient vibration. J. Sound Vib. 293, 409–425 (2006)

    Article  Google Scholar 

  6. Erturk, A., Inman, D.J.: An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 18, 025009 (2009)

    Article  Google Scholar 

  7. Liu, J.Q., Fang, H.B., Xu, Z.Y., Mao, X.H., Shen, X.C., Chen, D., Chen, D., Liao, H., Cai, B.C.: A MEMS-based piezoelectric power generator array for vibration energy harvesting. Microelectron. J. 39, 802–806 (2008)

    Article  Google Scholar 

  8. Marinkovic, B., Koser, H.: Demonstration of wide bandwidth energy harvesting from vibrations. Smart Mater. Struct. 21, 065006 (2012)

    Article  Google Scholar 

  9. Challa, V.R., Prasad, M.G., Shi, Y., Fisher, F.T.: A vibration energy harvesting device with bidirectional resonance frequency tenability. Smart Mater. Struct. 17, 015035 (2008)

    Article  Google Scholar 

  10. Kim, I.H., Jung, H.J., Lee, B.M., Jang, S.J.: Broadband energy-harvesting using a two degree-of-freedom vibrating body. Appl. Phys. Lett. 98, 214102 (2011)

    Article  Google Scholar 

  11. Jang, S.J., Rustighi, E., Brennan, M.J., Lee, Y.P., Jung, H.J.: Design of a 2DOF vibrational energy harvesting device. J. Intell. Mater. Syst. Struct. 22, 443–449 (2011)

    Article  Google Scholar 

  12. Brennan, M.J., Tang, B., Melo, G.P., Lopes Jr, V.: An investigation into the simultaneous use of a resonator as an energy harvester and a vibration absorber. J. Sound Vib. 333, 1331–1343 (2014)

    Article  Google Scholar 

  13. Luongo, A., Zulli, D.: Nonlinear energy sink to control elastic strings: the internal resonance case. Nonlinear Dyn. 81(1–2), 425–435 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  14. Tehrani, M.G., Elliott, S.J.: Extending the dynamic range of an energy harvester using nonlinear damping. J. Sound Vib. 333, 623–629 (2014)

    Article  Google Scholar 

  15. Cottone, F., Vocca, H., Gammaitoni, L.: Nonlinear energy harvesting. Phys. Rev. Lett. 102, 080601 (2009)

    Article  Google Scholar 

  16. McInnesa, C.R., Gormana, D.G., Cartmell, M.P.: Enhanced vibrational energy harvesting using nonlinear stochastic resonance. J. Sound Vib. 318, 655–662 (2008)

    Article  Google Scholar 

  17. Mann, B.P., Sims, N.D.: Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 319, 515–530 (2009)

    Article  Google Scholar 

  18. Stanton, S.C., Owens, B.A.M., Mann, B.P.: Harmonic balance analysis of the bistable piezoelectric inertial generator. J. Sound Vib. 331, 3617–3627 (2009)

    Article  Google Scholar 

  19. Stanton, S.C., McGehee, C.C., Mann, B.P.: Nonlinear dynamics for broadband energy harvesting: investigation of a bistable piezoelectric inertial generator. Phys. D 239, 640–653 (2010)

    Article  MATH  Google Scholar 

  20. Renno, J.M., Daqaq, M.F., Inman, D.J.: On the optimal energy harvesting from a vibration source. J. Sound Vib. 320, 386–405 (2009)

    Article  Google Scholar 

  21. Erturk, A., Inman, D.J.: Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 330, 2339–2353 (2011)

    Article  Google Scholar 

  22. Blarigan, L.V., Danzl, P., Moehlis, J.: A broadband vibrational energy harvester. Appl. Phys. Lett. 100, 253904 (2012)

    Article  Google Scholar 

  23. Harne, R.L., Thota, M., Wang, K.W.: Concise and high-fidelity predictive criteria for maximizing performance and robustness of bistable energy harvester. Appl. Phys. Lett. 102, 053903 (2013)

    Article  Google Scholar 

  24. Wu, Z., Harne, R.L., Wang, K.W.: Energy harvester synthesis via coupled linear-bistable system with multistable dynamics. J. Appl. Mech. 81, 061005 (2014)

    Article  Google Scholar 

  25. Harne, R.L., Wang, K.W.: Prospects for nonlinear energy harvesting systems designed near the elastic stability limit when driven by colored noise. J. Vib. Acoust. 136(2), 021009 (2014)

    Article  Google Scholar 

  26. Sardini, E., Serpelloni, M.: An efficient electromagnetic power harvesting device for low-frequency applications. Sens. Actuators A 172, 475–482 (2011)

    Article  Google Scholar 

  27. Ramlan, R., Brennan, M.J., Mace, B.R., Kovacic, I.: Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 59, 545–558 (2010)

    Article  MATH  Google Scholar 

  28. Ma, T.W., Zhang, H., Xu, N.S.: A novel parametrically excited non-linear energy harvester. Mech. Syst. Signal Process. 28, 323–332 (2012)

    Article  Google Scholar 

  29. Vijayan, K., Friswell, M.I., Khodaparast, H.H., Adhikari, S.: Non-linear energy harvesting from coupled impacting beams. Int. J. Mech. Sci. 96–97, 101–109 (2015)

    Article  Google Scholar 

  30. Sun, X.T., Jing, X.J., Xu, J., Cheng, L.: Vibration isolation via a scissor-like structured platform. J. Sound Vib. 333, 2404–2420 (2014)

  31. Xue, B.C.: Simulation study on scissor-like element vibrations. MSc Degree Thesis under supervision of X.J. Jing, The Hong Kong Polytechnic University (2012)

  32. Liu, C.C., Jing, X.J., Chen, Z.B.: Band stop vibration suppression using a passive X-shape structured lever-type isolation system. Mech. Syst. Signal Process. 68–69, 342–353 (2016)

    Article  Google Scholar 

  33. Alibert, J.J., Seppecher, P., Dell’isola, F.: Truss modular beams with deformation energy depending on higher displacement gradients. Math. Mech. Solids 8(1), 51–73 (2003)

  34. Dell’Isola, F., Lekszycki, T., Pawlikowski, M., Grygoruk, R., Greco, L.: Designing a light fabric metamaterial being highly macroscopically tough under directional extension: first experimental evidence. Z. Angew. Math. Phys. (2015). doi:10.1007/s00033-015-0556-4

    MathSciNet  MATH  Google Scholar 

  35. Placidi, L., Andreaus, U., Della Corte, A., Lekszycki, T.: Gedanken experiments for the determination of two-dimensional linear second gradient elasticity coefficients. Zeitschrift Fur Angewandte Mathematik Und Physik (2015). doi:10.1007/s00033-015-0588-9

    MathSciNet  MATH  Google Scholar 

  36. Li, B., Wang, S., Yuan, R., Zhi, C.: Dynamics analysis method study based on linear array deployable structure symmetry of scissor-like element. J. Northwest. Polytech. Univ. 33(4), 665–671 (2015)

    Google Scholar 

  37. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley Inter-science, New York (1979)

    MATH  Google Scholar 

  38. Rahimia, A., Zorlu, O., Muhtaroglu, A., Kulah, H.: An electromagnetic energy harvesting system for low frequency applications with a passive interface ASIC in standard CMOS. Sens. Actuators A 188, 158–166 (2012)

    Article  Google Scholar 

  39. Jing, X.J., Lang, Z.Q.: Frequency Domain Analysis and Design of Nonlinear Systems based on Volterra Series Expansion: A Parametric Characteristic Approach. Springer, Switzerland (2015)

    Book  MATH  Google Scholar 

  40. Xiao, Z., Jing, X.J., Cheng, L.: The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations. J. Sound Vib. 332(5), 1335–1354 (2013)

    Article  Google Scholar 

  41. Jing, X.J., Lang, Z.Q., Billings, S.A.: Nonlinear influence in the frequency domain: alternating series. Syst. Control Lett. 60(5), 295–309 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  42. Jing, X.J., Lang, Z.Q.: Frequency domain analysis of a dimensionless cubic nonlinear damping system subject to harmonic input. Nonlinear Dyn. 58(3), 469–485 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the support from a GRF project of Hong Kong RGC (Ref No.15206514), NSFC projects (No. 61374041 and 11402067) of China, Internal Competitive Research Grants of Hong Kong Polytechnic University, and a grant from the Innovation and Technology Commission of the HKSAR Government to the Hong Kong Branch of National Rail Transit Electrification and Automation Engineering Technology Research Center.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Hong Kong Polytechnic University, Hung Hom, HK, People’s Republic of China

    Chunchuan Liu & Xingjian Jing

  2. Hong Kong Branch of National Rail Transit Electrification and Automation Engineering Technology Research Center, Hong Kong, People’s Republic of China

    Chunchuan Liu

  3. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin, People’s Republic of China

    Chunchuan Liu

Authors
  1. Chunchuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xingjian Jing
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xingjian Jing.

Appendices

Appendix 1

$$\begin{aligned}&f_{11} ({\tilde{y}},{\tilde{\psi }})=\frac{l_1 \cos \theta _1 \left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) }{(2n_1 +1)\sqrt{l_1^2 -\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}}}\nonumber \\&\quad -\frac{\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) }{(2n_1 +1)}, \end{aligned}$$
(43)
$$\begin{aligned}&f_{12} ({\tilde{y}},{\tilde{\psi }})=\frac{l_2 \cos \theta _2 \left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) }{(2n_2 +1)\sqrt{l_2^2 -\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}}}\nonumber \\&-\frac{\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) }{2n_2 +1}, \end{aligned}$$
(44)
$$\begin{aligned}&f_{21} ({\tilde{y}},{\tilde{\psi }})=-\frac{dl_1 \cos \theta _1 \left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) }{(2n_1 +1)\sqrt{l_1^2 -\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}}}\nonumber \\&+\,\frac{d\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) }{2n_1 +1}, \end{aligned}$$
(45)
$$\begin{aligned}&f_{22} ({\tilde{y}},{\tilde{\psi }})=\frac{dl_2 \cos \theta _2 \left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) }{(2n_2 +1)\sqrt{l_2^2 -\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}}}\nonumber \\&-\frac{d\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) }{2n_2 +1}, \end{aligned}$$
(46)
$$\begin{aligned}&g_{11} ({\tilde{y}},{\tilde{\psi }})=\frac{\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}}{(2n_1 +1)^{2}\left[ {l_1^2 -\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}} \right] }, \end{aligned}$$
(47)
$$\begin{aligned}&g_{12} ({\tilde{y}},{\tilde{\psi }})=\frac{\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}}{(2n_2 +1)^{2}\left[ {l_2^2 -\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}} \right] }, \end{aligned}$$
(48)
$$\begin{aligned}&g_{21} ({\tilde{y}},{\tilde{\psi }})=\frac{d_1^2 \left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}}{(2n_1 +1)^{2}\left[ {l_1^2 -\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}} \right] },\nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned}&g_{22} ({\tilde{y}},{\tilde{\psi }})=\frac{d_1^2 \left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}}{(2n_2 +1)^{2}\left[ {l_2^2 -\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}} \right] }, \end{aligned}$$
(50)
$$\begin{aligned}&g_{01} ({\tilde{y}},{\tilde{\psi }})=-\frac{d_1 \left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}}{(2n_1 +1)^{2}\left[ {l_1^2 -\left( {l_1 \sin \theta _1 +\frac{{\tilde{y}}-{\tilde{\psi }}d_1 }{2n_1 +1}} \right) ^{2}} \right] }, \end{aligned}$$
(51)
$$\begin{aligned}&g_{02} ({\tilde{y}},{\tilde{\psi }})=\frac{d_1 \left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}}{(2n_2 +1)^{2}\left[ {l_2^2 -\left( {l_2 \sin \theta _2 +\frac{{\tilde{y}}+{\tilde{\psi }}d_1 }{2n_2 +1}} \right) ^{2}} \right] },\nonumber \\ \end{aligned}$$
(52)

Appendix 2

$$\begin{aligned} \varGamma _{11}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}, \end{aligned}$$
(53)
$$\begin{aligned} \varGamma _{12}= & {} \frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}},\end{aligned}$$
(54)
$$\begin{aligned} \varGamma _{21}= & {} \frac{6\tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 }\nonumber \\&+\frac{6\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 },\end{aligned}$$
(55)
$$\begin{aligned} \varGamma _{22}= & {} \frac{6\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }\nonumber \\&-\frac{6\tan \theta _1 }{(2n_1 +1)^{3}l_1^1 \cos ^{3}\theta _1 },\end{aligned}$$
(56)
$$\begin{aligned} \varGamma _{31}= & {} \frac{2\left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }\nonumber \\&+\frac{2\left( {3-2\cos 2\theta _2 } \right) }{(2n_2 +1)^{4}l_2^2 \cos \theta _2^6 },\end{aligned}$$
(57)
$$\begin{aligned} \varGamma _{32}= & {} \frac{2\left( {3-2\cos 2\theta _2 } \right) }{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 }\nonumber \\&-\frac{2\left( {3-2\cos 2\theta _1 } \right) }{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 },\end{aligned}$$
(58)
$$\begin{aligned} \varLambda _{01}= & {} \frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}}+\frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}},\end{aligned}$$
(59)
$$\begin{aligned} \varLambda _{02}= & {} \frac{4\tan ^{2}\theta _2 }{(2n_2 +1)^{2}}-\frac{4\tan ^{2}\theta _1 }{(2n_1 +1)^{2}},\end{aligned}$$
(60)
$$\begin{aligned} \varLambda _{11}= & {} \frac{8\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 }\nonumber \\&+\frac{8\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 },\end{aligned}$$
(61)
$$\begin{aligned} \varLambda _{12}= & {} \frac{8\tan \theta _2 }{(2n_2 +1)^{3}l_2 \cos ^{3}\theta _2 }\nonumber \\&-\frac{8\tan \theta _1 }{(2n_1 +1)^{3}l_1 \cos ^{3}\theta _1 },\end{aligned}$$
(62)
$$\begin{aligned} \varLambda _{21}= & {} \frac{4(1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }\nonumber \\&+\frac{4(1+3\sin ^{2}\theta _2 )}{(2n_1 +1)^{4}l_2^2 \cos ^{6}\theta _2 },\end{aligned}$$
(63)
$$\begin{aligned} \varLambda _{22}= & {} \frac{4(1+3\sin ^{2}\theta _2 )}{(2n_2 +1)^{4}l_2^2 \cos ^{6}\theta _2 }\nonumber \\&-\frac{4(1+3\sin ^{2}\theta _1 )}{(2n_1 +1)^{4}l_1^2 \cos ^{6}\theta _1 }. \end{aligned}$$
(64)

Appendix 3

$$\begin{aligned}&A_0 \varGamma _{11} \!+\!d_1 B_0 \varGamma _{12} \!+\!\left( A_0^2 \!+\!B_0^2 d_1^2 \!+\!\frac{A_1^2 \!+\!d_1^2 B_1^2 }{2}\right) \varGamma _{21}\nonumber \\&\quad +\,d_1 A_0 B_0 \varGamma _{22} +\left( A_0^3 +3d_1^2 A_0 B_0^2 \right. \nonumber \\&\left. \quad +\,\frac{3A_0 A_1^2 +3d_1^2 A_0 B_1^2 }{2}\right) \varGamma _{31} +\left( 3d_1 B_0 A_0^2 +d_1^3 B_0^3\right. \nonumber \\&\left. \quad +\,\frac{3d_1 A_1^2 B_0 +3d_1^3 B_0 B_1^2 }{2}\right) \varGamma _{32} +\left( d_1 A_1 B_1 \varGamma _{22} \right. \nonumber \\&\left. \quad +\,6d_1^2 A_1 B_0 B_1 \varGamma _{31} +6d_1 A_0 A_1 B_1 \varGamma _{32} \right) \nonumber \\&\quad \times \frac{\cos (\varphi _1 -\varphi _2 )}{2}=0, \end{aligned}$$
(65)
$$\begin{aligned}&A_0 \varGamma _{12} +d_1 B_0 \varGamma _{11} +d_1 A_0 B_0 \varGamma _{21}\nonumber \\&\left. \quad +\,\left( A_0^2 +d_1^2 B_0^2 +\frac{A_1^2 +d_1^2 B_1^2 }{2}\right) \right. \nonumber \\&\varGamma _{22} +\left( 3d_1 B_0 A_0^2 +d_1^3 B_0^3\right. \nonumber \\&\left. \quad +\,\frac{3d_1 A_1^2 B_0 +3d_1^3 B_0 B_1^2 }{2}\right) \varGamma _{31} +\left( A_0^3 +3d_1^2 A_0 B_0^2\right. \nonumber \\&\left. \quad +\,\frac{3A_0 A_1^2 +3d_1^2 A_0 B_1^2 }{2}\right) \varGamma _{32} \nonumber \\&\quad +\,\left( \frac{1}{2}d_1 A_1 B_1 \varGamma _{21} +3d_1^2 A_1 B_0 B_1 \varGamma _{32}\nonumber \right. \\&\left. \quad +\,3d_1 A_0 A_1 B_1 \varGamma _{31}\right) \cos (\varphi _1 -\varphi _2)=0, \end{aligned}$$
(66)
$$\begin{aligned}&A_1 \varGamma _{11} +2A_0 A_1 \varGamma _{21} +d_1 B_0 A_1 \varGamma _{22}\nonumber \\&\quad +\,\left( 3A_0^2 A_1 +3d_1^2 A_1 B_0^2 \right. \nonumber \\&\left. \quad +\,\frac{A_1^3 }{4}+\frac{3}{2}d_1^2 A_1 B_1^2 \right) \varGamma _{31} +6d_1 A_0 A_1 B_0 \varGamma _{32} \nonumber \\&\quad +\left[ d_1 B_1 \varGamma _{12} +2d_1^2 B_0 B_1 \varGamma _{21} +d_1 A_0 B_1 \varGamma _{22}\right. \nonumber \\&\left. \quad +\,6d_1^2 A_0 B_0 B_1 \varGamma _{31} +\left( 3d_1 A_0^2 B_1\right. \right. \nonumber \\&\left. \left. \quad +\,3d_1^3 B_0^2 B_1 +\frac{9}{4}d_1 A_1^2 B_1 \right. \right. \nonumber \\&\left. \left. \quad +\,\frac{1}{4}d_1^3 B_1^3 \right) \varGamma _{32} \right] \cos (\varphi _1 -\varphi _2 )\nonumber \\&\quad +\,\frac{3}{4}d_1^2 A_1 B_1^2 \varGamma _{31} \cos 2(\varphi _1 -\varphi _2 )\nonumber \\&\quad +\,2\xi \varOmega d_1 \left[ B_1 \varLambda _{02} +A_0 B_1 \varLambda _{12} \right. \nonumber \\&\left. \quad +\,d_1 B_0 B_1 \varLambda _{11} +2d_1 A_0 B_0 B_1 \varLambda _{21} +\left( A_0^2 B_1 \right. \right. \nonumber \\&\left. \left. \quad +\,d_1^2 B_0^2 B_1 +\frac{3}{4}A_1^2 B_1 +\frac{1}{4}d_1^2 B_1^3 \right) \varLambda _{22} \right] \sin (\varphi _1 -\varphi _2 ) \nonumber \\&\quad +\,\frac{1}{2}\xi \varOmega d_1^2 B_1^2 A_1 \varLambda _{21} \sin 2(\varphi _1 -\varphi _2 )\nonumber \\&\quad -\varOmega ^{2}A_1 -\varOmega ^{2}Z_0 \cos \varphi _1 =0, \end{aligned}$$
(67)
$$\begin{aligned}&\left[ d_1 B_1 \varGamma _{12} +2d_1^2 B_0 B_1 \varGamma _{21} +d_1 A_0 B_1 \varGamma _{22}\right. \nonumber \\&\left. \quad +\,6d_1^2 A_0 B_0 B_1 \varGamma _{31} + \left( 3d_1 A_0^2 B_1 \varGamma _{32}\right. \right. \nonumber \\&\left. \left. \quad +\,3d_1^3 B_0^2 B_1 +\frac{3}{4}d_1 A_1^2 B_1 \right. \right. \nonumber \\&\left. \left. \quad +\,\frac{1}{4}d_1^3 B_1^3 \right) \varGamma _{32} \right] \sin (\varphi _1 -\varphi _2 )\nonumber \\&\quad +\,\frac{3}{4}d_1^2 A_1 B_1^2 \varGamma _{31} \sin 2(\varphi _1 -\varphi _2 )\nonumber \\&\quad -\,2\xi \varOmega \left[ A_1 \varLambda _{01} +A_0 A_1 \varLambda _{11}\right. \nonumber \\&\left. \quad +\,d_1 B_0 A_1 \varLambda _{12} +\left( A_0^2 A_1 +d_1^2 B_0^2 A_1 +\frac{A_1^3 }{4}\right. \right. \nonumber \\&\left. \left. \quad +\,\frac{d_1^2 }{2}A_1 B_1^2 \right) \varLambda _{21} +2d_1 A_0 B_0 A_1 \right. \varLambda _{22} \nonumber \\&\left. \quad +\,\frac{d_1^2 }{4}A_1 B_1^2 \varLambda _{21} \cos 2(\varphi _1-\varphi _2 )\right] \nonumber \\&\quad -2\xi d_1 \varOmega \left[ B_1 \varLambda _{02} +A_0 B_1 \varLambda _{12}\right. \nonumber \\&\left. \quad +\,d_1 B_0 B_1 \varLambda _{11} +2d_1 A_0 B_0 B_1 \varLambda _{21} \right. \nonumber \\&\left. \quad +\left( A_0^2 B_1 +d_1^2 B_0^2 B_1 +\frac{d_1^2 }{4}B_1^3 \right) \varLambda _{22} \right] \cos (\varphi _1 -\varphi _2 )\nonumber \\&\quad -\varOmega ^{2}Z_0 \sin \varphi _1 =0 , \end{aligned}$$
(68)
$$\begin{aligned}&\beta d_1 \left\{ d_1 B_1 \varGamma _{11} +d_1 A_0 B_1 \varGamma _{21} +2d_1^2 B_0 B_1 \varGamma _{22}\right. \nonumber \\&\left. \quad +\left( 3d_1 A_0^2 B_1 +3d_1^3 B_0^2 B_1 +\frac{3}{2}d_1 \varGamma _{31} A_1^2 B_1 +\frac{1}{4}d_1^3 B_1^3 \right) \varGamma _{31} \right. \nonumber \\&\left. \quad +\,6d_1^2 A_0 B_0 B_1 \varGamma _{32} +\left[ A_1 \varGamma _{12} +d_1 B_0 A_1 \varGamma _{21}\right. \right. \nonumber \\&\left. \left. \quad +\,2A_0 A_1 \varGamma _{22} +6d_1 A_0 A_1 B_0 \varGamma _{31} +\left( 3A_0^2 A_1 +3d_1^2 A_1 B_0^2 \right. \right. \right. \nonumber \\&\left. \left. \left. \quad +\,\frac{A_1^3 }{4}+\frac{9}{4}d_1^2 A_1 B_1^2 \right) \varGamma _{32} \right] \cos (\varphi _1 -\varphi _2 )\right. \nonumber \\&\left. \quad +\,\frac{3}{4}d_1 A_1^2 B_1 \varGamma _{31} \cos 2(\varphi _1 -\varphi _2 )\right. \nonumber \\&\left. \quad -\,2\xi \varOmega \left[ A_1 \varLambda _{02} +d_1 B_0 A_1 \varLambda _{11} \right. \right. \nonumber \\&\left. \left. \quad +\,A_0 A_1 \varLambda _{12} +2d_1 A_0 B_0 A_1 \varLambda _{21} +\left( A_0^2 A_1 +d_1^2 B_0^2 A_1\right. \right. \right. \nonumber \\&\left. \left. \left. \quad +\,\frac{1}{4}A_1^3 +\frac{1}{2}d_1^2 B_1^2 A_1 \right) \varLambda _{22} \right] \sin (\varphi _1 -\varphi _2 ) \right. \nonumber \\&\left. \quad -\xi \varOmega d_1 A_1^2 B_1 \varLambda _{21} \sin 2(\varphi _1 -\varphi _2 )\right\} \nonumber \\&\quad -\varOmega ^{2}B_1 -\varOmega ^{2}\Psi _0 \cos \varphi _2=0, \end{aligned}$$
(69)
$$\begin{aligned}&\beta d_1 \left\{ \left[ A_1 \varGamma _{12} +2A_0 A_1 \varGamma _{22} +d_1 B_0 A_1 \varGamma _{21}\right. \right. \nonumber \\&\left. \left. \quad +\,6d_1 A_0 A_1 B_0 \varGamma _{31} -\frac{3}{4}d_1 A_1^2 B_1 \varGamma _{31} \sin 2(\varphi _1 -\varphi _2 ) \right. \right. \nonumber \\&\left. \left. \quad +\left( 3A_0^2 A_1 +3d_1^2 A_1 B_0^2 +\frac{A_1^3 }{4}\right) \varGamma _{32} \right] \sin (\varphi _1 -\varphi _2 )\right. \nonumber \\&\left. \quad +\,2\xi d_1 \varOmega \left( B_1 \varLambda _{01} +A_0 B_1 \varLambda _{11} +d_1 B_0 B_1 \varLambda _{12} \right. \right. \nonumber \\&\left. \left. \quad +\,A_0^2 B_1 \varLambda _{21} +d_1^2 B_0^2 B_1 \varLambda _{21} +2d_1 A_0 B_0 B_1 \varLambda _{22}\right. \right. \nonumber \\&\left. \left. \quad +\,\frac{1}{2}A_1^2 B_1 \varLambda _{21} +\frac{1}{4}d_1^2 B_1^3 \varLambda _{21} \right) +2\xi \varOmega \left[ \left( \varLambda _{02} A_1 \right. \right. \right. \nonumber \\&\left. \left. \left. \quad +\,A_0 A_1 \varLambda _{12} +d_1 B_0 A_1 \varLambda _{11} +A_0^2 A_1 \varLambda _{22} +d_1^2 B_0^2 A_1 \varLambda _{22}\right. \right. \right. \nonumber \\&\left. \left. \left. \quad +\,2d_1 A_0 B_0 A_1 \varLambda _{21} +\frac{A_1^3 }{4}\varLambda _{22} \right. \right. \right. \nonumber \\&\left. \left. \left. \quad +\,\frac{3}{4}d_1^2 B_1^2 A_1 \varLambda _{22} \right) \cos (\varphi _1 -\varphi _2 )\right. \right. \nonumber \\&\left. \left. \quad +\,\frac{1}{2}d_1 A_1^2 B_1 \varLambda _{21} \cos 2(\varphi _1 -\varphi _2 )\right] \right\} +\varOmega ^{2}\Psi _0 \sin \varphi _2 =0,\nonumber \\ \end{aligned}$$
(70)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Jing, X. Vibration energy harvesting with a nonlinear structure. Nonlinear Dyn 84, 2079–2098 (2016). https://doi.org/10.1007/s11071-016-2630-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2630-7

Keywords

Search

Navigation