Skip to main content
SpringerLink
Log in

A neural network model of spontaneous up and down transitions

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

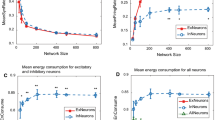
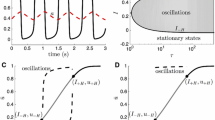
Spontaneous periodic up and down transitions are considered to be a significant phenomenon that is characteristic of slow-wave sleep. We studied a neural network model of spontaneous up and down transitions based on our former study of a single-neuron model. We expanded the model by using two types of neurons—excitatory and inhibitory neurons—and redefining the connecting function between two neurons instead of assuming a constant connection, so that the model is closer to the in vivo network. Using this model, we studied the relationship between the transitions and network parameters such as size, structure and the ratio of excitatory to inhibitory neurons. We found that the network parameters have little impact on these spontaneous periodic up and down transitions. However, the intrinsic currents were found to play a leading role in the process. Then, we studied the transitions in the presence of stimulation and found that the addition of stimulation did have an effect on the network transitions. Through the observation and analysis of the findings, we have tried to explain the dynamics of up and down transitions and to lay the foundation for future work on the role of these transitions in cortex activity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Parga, N., Abbott, L.F.: Network model of spontaneous activity exhibiting synchronous transitions between up and down states. Front. Neurosci. 1(1), 57 (2007)

    Article  Google Scholar 

  2. Anderson, J., Lampl, I., Reichova, I., Carandini, M., Ferster, D.: Stimulus dependence of two-state fluctuations of membrane potential in cat visual cortex. Nat. Neurosci. 3(6), 617–621 (2000)

    Article  Google Scholar 

  3. Lampl, I., Reichova, I., Ferster, D.: Synchronous membrane potential fluctuations in neurons of the cat visual cortex. Neuron 22(2), 361–374 (1999)

    Article  Google Scholar 

  4. Steriade, M., Nuñez, A., Amzica, F.: Intracellular analysis of relations between the slow (1 Hz) neocortical oscillation and other sleep rhythms of the electroencephalogram. J. Neurosci. 13(8), 3266–3283 (1993)

    Google Scholar 

  5. Petersen, C.C., Hahn, T.T., Mehta, M., Grinvald, A., Sakmann, B.: Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex. Proc. Natl. Acad. Sci. 100(23), 13638–13643 (2003)

    Article  Google Scholar 

  6. Araki, O.: Computer simulations of synchrony and oscillations evoked by two coherent inputs. Cogn. Neurodyn. 7(2), 133–141 (2013)

    Article  Google Scholar 

  7. Ma, J., Hu, B., Wang, C., Jin, W.: Simulating the formation of spiral wave in the neuronal system. Nonlinear Dyn. 73(1), 73–83 (2013)

    Article  MathSciNet  Google Scholar 

  8. Wang, G., Jin, W., Wang, A.: Synchronous firing patterns and transitions in small-world neuronal network. Nonlinear Dyn. 81(3), 1453–1458 (2015)

    Article  MathSciNet  Google Scholar 

  9. Zhou, J., Wu, Q., Xiang, L.: Impulsive pinning complex dynamical networks and applications to firing neuronal synchronization. Nonlinear Dyn. 69(3), 1393–1403 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Liu, Y., Wang, R., Zhang, Z., Jiao, X.: Analysis of stability of neural network with inhibitory neurons. Cogn. Neurodyn. 4(1), 61–68 (2010)

    Article  Google Scholar 

  11. Gu, H., Pan, B., Li, Y.: The dependence of synchronization transition processes of coupled neurons with coexisting spiking and bursting on the control parameter, initial value, and attraction domain. Nonlinear Dyn. 82(3), 1191–1210 (2015)

    Article  MathSciNet  Google Scholar 

  12. Njap, F., Claussen, J.C., Moser, A., Hofmann, U.G.: Modeling effect of GABAergic current in a basal ganglia computational model. Cogn. Neurodyn. 6(4), 333–341 (2012)

    Article  Google Scholar 

  13. Zheng, C., Zhang, T.: Alteration of phase-phase coupling between theta and gamma rhythms in a depression-model of rats. Cogn. Neurodyn. 7(2), 167–172 (2013)

    Article  Google Scholar 

  14. Wang, Q., Zheng, Y., Ma, J.: Cooperative dynamics in neuronal networks. Chaos Solions Fractals 56(7), 19–27 (2013)

    Google Scholar 

  15. Perc, M.: Spatial coherence resonance in excitable media. Phys. Rev. E 72(1), 016207 (2005)

    Article  MathSciNet  Google Scholar 

  16. Gosak, M., Marhl, M., Perc, M.: Spatial coherence resonance in excitable biochemical media induced by internal noise. Biophys. Chem. 128(2), 210–214 (2007)

    Article  MATH  Google Scholar 

  17. Perc, M., Gosak, M., Marhl, M.: Periodic calcium waves in coupled cells induced by internal noise. Chem. Phys. Lett. 437(1), 143–147 (2007)

    Article  Google Scholar 

  18. DiFrancesco, D.: Pacemaker mechanisms in cardiac tissue. Annu. Rev. Physiol. 55(1), 455–472 (1993)

    Article  Google Scholar 

  19. Lüthi, A., McCormick, D.A.: H-current: properties of a neuronal and network pacemaker. Neuron 21(1), 9–12 (1998)

    Article  Google Scholar 

  20. Pape, H.C.: Queer current and pacemaker: the hyperpolarization-activated cation current in neurons. Annu. Rev. Physiol. 58(1), 299–327 (1996)

    Article  Google Scholar 

  21. Dickson, C.T., Magistretti, J., Shalinsky, M.H., Fransén, E., Hasselmo, M.E., Alonso, A.: Properties and role of Ih in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J. Neurophysiol. 83(5), 2562–2579 (2000)

    Google Scholar 

  22. Wilson, A., Cowan, J.D.: Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12(1), 1–24 (1972)

    Article  Google Scholar 

  23. Compte, A., Sanchez-Vives, M.V., McCormick, D.A., Wang, X.J.: Cellular and network mechanisms of slow oscillatory activity (1 Hz) and wave propagations in a cortical network model. J. Neurophysiol. 89, 2707–2725 (2003)

    Article  Google Scholar 

  24. Holcman, D., Tsodyks, M.: The emergence of up and down states in cortical networks. PLOS Comput. Biol. 2, 174–181 (2006)

    Article  Google Scholar 

  25. Yang, Z., Wang, Q., Danca, M.F., Zhang, J.: Complex dynamics of compound bursting with burst episode composed of different bursts. Nonlinear Dyn. 70(3), 2003–2013 (2012)

    Article  MathSciNet  Google Scholar 

  26. Ma, J., Tang, J.: A review for dynamics of collective behaviors of network of neurons. Sci. China Technol. Sci. 58, 2038–2045 (2015)

    Article  Google Scholar 

  27. Xu, X., Wang, R.: Neurodynamics of up and down transitions in a single neuron. Cogn. Neurodyn. 8(6), 509–515 (2014)

    Article  Google Scholar 

  28. Xu, X., Wang, R.: Neurodynamics of up and down transitions in network model. Abstr. Appl. Anal. 2013, 9 (2013). doi:10.1155/2013/486178

  29. Wang, R., Zhang, Z., Chen, G.: Energy coding and energy functions for local activities of the brain. Neurocomputing 73(1), 139–150 (2009)

    Article  Google Scholar 

  30. Wang, R., Zhang, Z., Chen, G.: Energy function and energy evolution on neuronal populations. Neural Netw. IEEE Trans. 19(3), 535–538 (2008)

    Article  Google Scholar 

  31. Wang, R., Zhang, Z.: Energy coding in biological neural networks. Cogn. Neurodyn. 1(3), 203–212 (2007)

    Article  Google Scholar 

  32. Wang, Q.Y., Murks, A., Perc, M., Lu, Q.S.: Taming desynchronized bursting with delays in the Macaque cortical network. Chin. Phys. B 20(4), 040504 (2011)

    Article  Google Scholar 

  33. Loewenstein, Y., Mahon, S., Chadderton, P., Kitamura, K., Sompolinsky, H., Yarom, Y., Häusser, M.: Bistability of cerebellar Purkinje cells modulated by sensory stimulation. Nat. Neurosci. 8(2), 202–211 (2005)

    Article  Google Scholar 

  34. Koch, C., Segev, I.: Methods in neuronal modeling: from ions to networks. MIT Press, Cambridge (1998)

    Google Scholar 

  35. Destexhe, A., Mainen, Z.F., Sejnowski, T.J.: Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J. Comput. Neurosci. 1(3), 195–230 (1994)

    Article  Google Scholar 

  36. Bazhenov, M., Timofeev, I., Steriade, M., Sejnowski, T.J.: Potassium model for slow (2–3 Hz) in vivo neocortical paroxysmal oscillations. J. Neurophysiol. 92(2), 1116 (2004)

    Article  Google Scholar 

  37. Ermentrout, T.J., Terman, D.H.: Mathematical foundations of neuroscience. Springer, Berlin (2010)

  38. Li, C.Y., Poo, M.M., Dan, Y.: Burst spiking of a single cortical neuron modifies global brain state. Science 324(5927), 643–646 (2009)

    Article  Google Scholar 

Download references

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 11232005) and The Ministry of Education Doctoral Foundation (No. 20120074110020).

Author information

Authors and Affiliations

  1. Institute for Cognitive Neurodynamics, East China University of Science and Technology, Shanghai, 200237, People’s Republic of China

    Xuying Xu, Li Ni & Rubin Wang

Authors
  1. Xuying Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Ni
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rubin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rubin Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, X., Ni, L. & Wang, R. A neural network model of spontaneous up and down transitions. Nonlinear Dyn 84, 1541–1551 (2016). https://doi.org/10.1007/s11071-015-2587-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2587-y

Keywords

Search

Navigation