Skip to main content
SpringerLink
Log in

Stability, bifurcation, and synchronization of delay-coupled ring neural networks

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

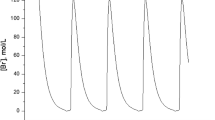
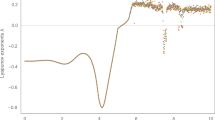
This paper studies the nonlinear dynamics of coupled ring networks each with an arbitrary number of neurons. Different types of time delays are introduced into the internal connections and couplings. Local and global asymptotical stability of the coupled system is discussed, and sufficient conditions for the existence of different bifurcated oscillations are given. Numerical simulations are performed to validate the theoretical results, and interesting neuronal activities are observed, such as rest state, synchronous oscillations, asynchronous oscillations, and multiple switches of the rest states and different oscillations. It is shown that the number of neurons in the sub-networks plays an important role in the network characteristics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Yamaguchi, S., Isejima, H., Matsuo, T., Okura, R., Yagita, K., Kobayashi, M., Okamura, H.: Synchronization of cellular clocks in the suprachiasmatic nucleus. Science 302(5649), 1408–1412 (2003)

    Article  Google Scholar 

  2. Nijmeijer, H., Rodriguez-Angeles, A.: Synchronization of mechanical systems. World Scientific Publishing, Singapore (2003)

    MATH  Google Scholar 

  3. Mao, X.C.: Stability switches, bifurcation, and multi-stability of coupled networks with time delays. Appl. Math. Comput. 218(11), 6263–6274 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  4. Murguia, C., Fey, R.H.B., Nijmeijer, H.: Network synchronization of time-delayed coupled nonlinear systems using predictor-based diffusive dynamic couplings. Chaos 25(2), 023108 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  5. Emelianova, Y.P., Emelyanov, V.V., Ryskin, N.M.: Synchronization of two coupled multimode oscillators with time-delayed feedback. Commun. Nonlinear Sci. Numer. Simulat 19(10), 3778–3791 (2014)

    Article  MathSciNet  Google Scholar 

  6. Louzada, V.H.P., Araujo, N.A.M., Andrade, J.S., Herrmann, H.J.: Breathing synchronization in interconnected networks. Sci. Rep. 3, 3289 (2013)

    Article  Google Scholar 

  7. Weicker, L., Erneux, T., Keuninckx, L., Danckaert, J.: Analytical and experimental study of two delay-coupled excitable units. Phys. Rev. E 89(1), 012908 (2014)

    Article  Google Scholar 

  8. Flunkert, V., Fischer, I., Fischer, I.: Dynamics, control and information in delay-coupled systems: an overview. Philos. Trans. R. Soc. A 371(1999), 20120465 (2013)

    Article  MathSciNet  Google Scholar 

  9. Hu, H.Y., Wang, Z.H.: Dynamics of controlled mechanical systems with delayed feedback. Springer, Heidelberg (2002)

    Book  MATH  Google Scholar 

  10. Sipahi, R., Niculescu, S.-I., Abdallah, C.T., Michiels, W., Gu, K.: Stability and stabilization of systems with time delay: limitations and opportunities. IEEE Control Syst. Mag. 31(1), 38–65 (2011)

    Article  MathSciNet  Google Scholar 

  11. Orosz, G., Wilson, R.E., Stepan, G.: Traffic jams: dynamics and control. Philos. Trans. R. Soc. A 368(1928), 4455–4479 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  12. Shepherd, G.M.: Neurobiology. Oxford University Press, New York (1983)

    Google Scholar 

  13. Murray, J.D.: Mathematical Biology. Springer, New York (1990)

    MATH  Google Scholar 

  14. Marcus, C.M., Westervelt, R.M.: Stability of analog neural network with delay. Phys. Rev. A 39, 347–359 (1989)

    Article  MathSciNet  Google Scholar 

  15. Hopfield, J.J.: Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 81, 3088–3092 (1984)

    Article  Google Scholar 

  16. Timme, M., Wolf, F., Geisel, T.: Coexistence of regular and irregular dynamics in complex networks of pulse-coupled oscillators. Phys. Rev. Lett. 89, 258701 (2002)

    Article  Google Scholar 

  17. Punetha, N., Prasad, A., Ramaswamy, R.: Phase-locked regimes in delay-coupled oscillator networks. Chaos 24(4), 043111 (2014)

    Article  MathSciNet  Google Scholar 

  18. Popovych, O.V., Yanchuk, S., Tass, P.A.: Delay- and coupling-induced firing patterns in oscillatory neural loops. Phys. Rev. Lett. 107(22), 228102 (2011)

    Article  Google Scholar 

  19. Soriano, M.C., Flunkert, V., Fischer, I.: Relation between delayed feedback and delay-coupled systems and its application to chaotic lasers. Chaos 23(4), 043133 (2013)

    Article  MATH  Google Scholar 

  20. Sadeghi, S., Valizadeh, A.: Synchronization of delayed coupled neurons in presence of inhomogeneity. J. Comput. Neurosci. 36(1), 55–66 (2014)

    Article  MathSciNet  Google Scholar 

  21. Ge, J.H., Xu, J.: Computation of synchronized periodic solution in a BAM network with two delays. IEEE Trans. Neural Netw. 21(3), 439–450 (2010)

    Article  MathSciNet  Google Scholar 

  22. Ying, J., Guo, S., He, Y.: Multiple periodic solutions in a delay-coupled system of neural oscillators. Nonlinear Anal. Real World Appl. 12(5), 2767–2783 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  23. Song, Y.L.: Hopf bifurcation and spatio-temporal patterns in delay-coupled van der Pol oscillators. Nonlinear Dyn. 63(1–2), 223–237 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wirkus, S., Rand, R.: The dynamics of two coupled van der Pol oscillators with delay coupling. Nonlinear Dyn. 30(3), 205–221 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  25. Correa, D.P.F., Wulff, C., Piqueira, J.R.C.: Symmetric bifurcation analysis of synchronous states of time-delayed coupled Phase-Locked Loop oscillators. Commun. Nonlinear Sci. Numer. Simul. 22(1–3), 793–820 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Shen, Z., Zhang, C.: Double Hopf bifurcation of coupled dissipative Stuart–Landau oscillators with delay. Appl. Math. Comput. 227, 553–566 (2014)

    Article  MathSciNet  Google Scholar 

  27. Usacheva, S.A., Ryskin, N.M.: Phase locking of two limit cycle oscillators with delay coupling. Chaos 24(2), 023123 (2014)

    Article  MathSciNet  Google Scholar 

  28. Caceres, M.O.: Time-delayed coupled logistic capacity model in population dynamics. Phys. Rev. E 90(2), 022137 (2014)

    Article  MathSciNet  Google Scholar 

  29. Campbell, S.A., Edwards, R., Van Den Driessche, P.: Delayed coupling between two neural network loops. SIAM. J. Appl. Math. 65(1), 316–335 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Cheng, C.: Induction of Hopf bifurcation and oscillation death by delays in coupled networks. Phys. Lett. A 374(2), 178–185 (2009)

  31. Song, Z.G., Xu, J.: Stability switches and multistability coexistence in a delay-coupled neural oscillators system. J. Theor. Biol. 313, 98–114 (2012)

    Article  MathSciNet  Google Scholar 

  32. Jiang, Y., Guo, S.: Linear stability and Hopf bifurcation in a delayed two-coupled oscillator with excitatory-to-inhibitory connection. Nonlinear Anal. Real World Appl. 11(3), 2001–2015 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Peng, Y., Song, Y.: Stability switches and Hopf bifurcations in a pair of identical tri-neuron network loops. Phys. Lett. A 373(20), 1744–1749 (2009)

    Article  MATH  Google Scholar 

  34. Mao, X.C.: Stability and Hopf bifurcation analysis of a pair of three-neuron loops with time delays. Nonlinear Dynam. 68(1), 151–159 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  35. Song, Y., Tade, M.O., Zhang, T.: Bifurcation analysis and spatio-temporal patterns of nonlinear oscillations in a delayed neural network with unidirectional coupling. Nonlinearity 22(5), 975–1001 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  36. Kandel, E.R., Schwartz, J.H., Jessell, T.M.: Principles of neural science. McGraw-Hill, New York (2000)

    Google Scholar 

  37. Graybiel, A.M.: Basal ganglia-input, neural activity, and relation to the cortex. Curr. Opin. Neurobiol. 1(4), 644–651 (1991)

    Article  Google Scholar 

  38. Nana, B., Woafo, P.: Synchronization in a ring of four mutually coupled van der Pol oscillators: theory and experiment. Phys. Rev. E 74(4), 046213 (2006)

    Article  Google Scholar 

  39. Hoppensteadt, F.C., Izhikevich, E.M.: Weakly connected neural networks. Springer, New York (1997)

    Book  MATH  Google Scholar 

  40. Hisi, A.N.S., Guimaraes, P.R., de Aguiar, M.A.M.: The role of predator overlap in the robustness and extinction of a four species predator–prey network. Phys. A 389(21), 4725–4733 (2010)

    Article  Google Scholar 

  41. Xu, X.: Complicated dynamics of a ring neural network with time delays. J. Phys. A 41(3), 035102 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  42. Guo, S.J., Huang, L.H.: Hopf bifurcating periodic orbits in a ring of neurons with delays. Phys. D 183, 19–44 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  43. Campbell, S.A., Yuan, Y., Bungay, S.D.: Equivariant Hopf bifurcation in a ring of identical cells with delayed coupling. Nonlinearity 18(6), 2827–2846 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  44. Burić, N., Grozdanović, I., Vasović, N.: Excitable systems with internal and coupling delays. Chaos Soliton Fractals 36(4), 853–861 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  45. Song, Y., Makarov, V.A., Velarde, M.G.: Stability switches, oscillatory multistability, and spatio-temporal patterns of nonlinear oscillations in recurrently delay coupled neural networks. Biol. Cybern. 101(2), 147–167 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  46. Tass, P.A., Hauptmann, C.: Therapeutic modulation of synaptic connectivity with desynchronizing brain stimulation. Int. J. Psychophysiol. 64(1), 53–61 (2007)

    Article  Google Scholar 

Download references

Acknowledgments

The authors thank the financial support from the National Natural Science Foundation of China under Grant Nos. 11472097 and 11002047, the State Key Laboratory of Mechanics and Control of Mechanical Structures (Nanjing University of Aeronautics and Astronautics) under Grant No. MCMS-0113G01, and the Fundamental Research Funds for the Central Universities under Grant No. 2015B18214. They thank the anonymous reviewers for their helpful comments and suggestions that have helped to improve the presentation of this paper.

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, College of Mechanics and Materials, Hohai University, Nanjing, 210098, China

    Xiaochen Mao

  2. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Xiaochen Mao & Zaihua Wang

  3. Institute of Science, PLA University of Science and Technology, Nanjing, 211101, China

    Zaihua Wang

Authors
  1. Xiaochen Mao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zaihua Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaochen Mao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mao, X., Wang, Z. Stability, bifurcation, and synchronization of delay-coupled ring neural networks. Nonlinear Dyn 84, 1063–1078 (2016). https://doi.org/10.1007/s11071-015-2550-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2550-y

Keywords

Search

Navigation