Abstract
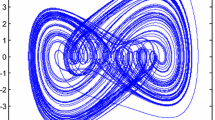
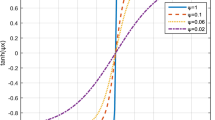
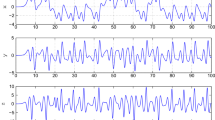
This paper studies the fractional-order disturbance observer (FODO)-based adaptive sliding mode synchronization control for a class of fractional-order chaotic systems with unknown bounded disturbances. To handle unknown disturbances, the nonlinear FODO is explored for the fractional-order chaotic system. By choosing the appropriate control gain parameter, the disturbance observer can approximate the disturbance well. On the basis of the sliding mode control technique, a simple sliding mode surface is defined. A synchronization control scheme incorporating the introduced sliding mode surface and the designed disturbance observer is then developed. Under the control of the synchronization scheme, a good synchronization performance is realized between two identical fractional-order chaotic systems with different initial conditions. Finally, the numerical simulation results illustrate the effectiveness of the developed synchronization control scheme for fractional-order chaotic systems in the presence of external disturbances.




Similar content being viewed by others
References
Podlubny, I.: Fractional-order systems and \({PI^\lambda }{D^\mu }\)-controllers. IEEE Trans. Autom. Control 44, 208–214 (1999)
Moghadasianx, M., Betin, F., Yazidi, A., Capolino, G.A., Kianinezhad, R.: Position control of six-phase induction machine using fractional-order controller. International Conference on Electrical Machines (ICEM), Marseille, France, pp. 1048–1054 (2012)
Das, S., Pan, I.: Fractional Order Signal Processing: Introductory Concepts and Applications. Springer, New York (2012)
Zhang, D., Yu, L.: Exponential state estimation for Markovian jumping neural networks with time-varying discrete and distributed delays. Neural Netw. 35, 103–111 (2012)
Zhang, D., Yu, L., Wang, Q.G., Ong, C.J.: Estimator design for discrete-time switched neural networks with asynchronous switching and time-varying delay. IEEE Trans. Neural Netw. Learn. Syst. 23, 827–834 (2012)
Zhang, D., Yu, L.: Passivity analysis for discrete-time switched neural networks with various activation functions and mixed time delays. Nonlinear Dyn. 67, 403–411 (2012)
Zhang, D., Yu, L.: Passivity analysis for stochastic Markovian switching genetic regulatory networks with time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 16, 2985–2992 (2011)
Shokooh, A., Suáez, L.: A comparison of numerical methods applied to a fractional model of damping materials. J. Vib. Control 5, 331–354 (1999)
West, B., Bologna, M., Grigolini, P.: Physics of Fractal Operators. Springer, New York (2003)
Dadras, S., Momeni, H.R.: Control of a fractional-order economical system via sliding mode. Phys. A Stat. Mech. Appl. 389, 2434–2442 (2010)
El-Sayed, A.M.A., Rida, S.Z., Arafa, A.A.M.: Exact solutions of fractional-order biological population model. Commun. Theor. Phys. 52, 992–996 (2009)
Chen, W.C.: Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 36, 1305–1314 (2008)
Lu, J.G.: Chaotic dynamics of the fractional-order Lü system and its synchronization. Phys. Lett. A 354, 305–311 (2006)
Wang, X.Y., Wang, M.J.: Dynamic analysis of the fractional-order Liu system and its synchronization. Chaos Interdiscip. J. Nonlinear Sci. 17, 033106 (2007)
Liu, L., Liu, C.X., Zhang, Y.B.: Experimental verification of a four-dimensional Chua’s system and its fractional order chaotic attractors. Int. J. Bifurc. Chaos 19, 2473–2486 (2009)
Wang, X.Y., Song, J.M.: Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control. Commun. Nonlinear Sci. Numer. Simul. 14, 3351–3357 (2009)
Min, F.H., Yu, Y., Ge, C.J.: Circuit implementation and tracking control of the fractional-order hyper-chaotic Lü system. Acta Phys. Sin. 58, 1456–1461 (2009)
Liu, L., Liang, D.L., Liu, C.X.: Nonlinear state-observer control for projective synchronization of a fractional-order hyperchaotic system. Nonlinear Dyn. 69, 1929–1939 (2012)
Liu, L., Liu, C.X.: Theoretical analysis and circuit verification for fractional-order chaotic behavior in a new hyperchaotic system. Math. Probl. Eng. 2014, 682408 (2014)
Pecora, L.M., Carroll, T.L.: Synchronization in chaotic systems. Phys. Rev. Lett. 64, 821–824 (1990)
Carroll, T.L., Pecora, L.M.: Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 38, 453–456 (1991)
Xi, H.L., Yu, S.M., Zhang, R.X., Xu, L.: Adaptive impulsive synchronization for a class of fractional-order chaotic and hyperchaotic systems. Optik Int. J. Light Electron Opt. 125, 2036–2040 (2014)
Bhalekar, S., Daftardar-Gejji, V.: Synchronization of different fractional order chaotic systems using active control. Commun. Nonlinear Sci. Numer. Simul. 15, 3536–3546 (2010)
Yang, L.X., Jiang, J.: Adaptive synchronization of drive-response fractional-order complex dynamical networks with uncertain parameters. Commun. Nonlinear Sci. Numer. Simul. 19, 1496–1506 (2014)
Peng, G.J., Jiang, Y.L., Chen, F.: Generalized projective synchronization of fractional order chaotic systems. Phys. A Stat. Mech. Appl. 387, 3738–3746 (2008)
Wu, C.J., Zhang, Y.B., Yang, N.N.: The synchronization of a fractional order hyperchaotic system based on passive control. Chin. Phys. B 20, 060505 (2011)
Šabanovic, A.: Variable structure systems with sliding modes in motion control—a survey. IEEE Trans. Ind. Inform. 7, 212–223 (2011)
Shi, P., Xia, Y.Q., Liu, G.P., Rees, D.: On designing of sliding-mode control for stochastic jump systems. IEEE Trans. Autom. Control 51, 97–103 (2006)
Zhang, J.H., Shi, P., Xia, Y.Q.: Robust adaptive sliding-mode control for fuzzy systems with mismatched uncertainties. IEEE Trans. Fuzzy Syst. 18, 700–711 (2010)
Jiang, B., Shi, P., Mao, Z.H.: Sliding mode observer-based fault estimation for nonlinear networked control systems. Circuits Syst. Signal Process. 30, 1–16 (2011)
Gao, Z.F., Jiang, B., Shi, P., Qian, M.S., Lin, J.X.: Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique. J. Frankl. Inst. 349, 1543–1560 (2012)
Tavazoei, M.S., Haeri, M.: Synchronization of chaotic fractional-order systems via active sliding mode controller. Phys. A Stat. Mech. Appl. 387, 57–70 (2008)
Wang, B., Zhou, Y.G., Xue, J.Y., Zhu, D.L.: Active sliding mode for synchronization of a wide class of four-dimensional fractional-order chaotic systems. ISRN Appl. Math. 2014, 472371 (2014)
Hosseinnia, S.H., Ghaderi, R., Ranjbar, A.N., Mahmoudian, M., Momani, S.: Sliding mode synchronization of an uncertain fractional order chaotic system. Comput. Math. Appl. 59, 1637–1643 (2010)
Aghababa, M.P.: Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller. Commun. Nonlinear Sci. Numer. Simul. 17, 2670–2681 (2012)
Zhang, L.G., Yan, Y.: Robust synchronization of two different uncertain fractional-order chaotic systems via adaptive sliding mode control. Nonlinear Dyn. 76, 1761–1767 (2014)
Li, C.L., Su, K.L., Wu, L.: Adaptive sliding mode control for synchronization of a fractional-order chaotic system. J. Comput. Nonlinear Dyn. 8, 031005 (2013)
Liu, L., Ding, W., Liu, C.X., Ji, H.G., Cao, C.Q.: Hyperchaos synchronization of fractional-order arbitrary dimensional dynamical systems via modified sliding mode control. Nonlinear Dyn. 76, 2059–2071 (2014)
Chen, W.H.: Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 9, 706–710 (2004)
Chen, W.H., Ballance, D.J., Gawthrop, P.J., O’Reilly, J.: A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 47, 932–938 (2000)
Chen, M., Chen, W.H., Wu, Q.X.: Adaptive fuzzy tracking control for a class of uncertain MIMO nonlinear systems using disturbance observer. Sci. China Inf. Sci. 57, 012207 (2014)
Chen, M., Yu, J.: Disturbance observer-based adaptive sliding mode control for near-space vehicles. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2268-x
Chen, M., Yu, J.: Adaptive dynamic surface control of nsvs with input saturation using a disturbance observer. Chin. J. Aeronaut. 28, 853–864 (2015)
Chen, M., Ren, B.B., Wu, Q.X., Jiang, C.S.: Anti-disturbance control of hypersonic flight vehicles with input saturation using disturbance observer. Sci. China Inf. Sci. 58, 070202 (2015)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, New York (2006)
Aguila-Camacho, N., Duarte-Mermoud, M.A., Gallegos, J.A.: Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 19, 2951–2957 (2014)
Li, L., Sun, Y.G.: Adaptive fuzzy control for nonlinear fractional-order uncertain systems with unknown uncertainties and external disturbance. Entropy 17, 5580–5592 (2015)
Li, C.P., Deng, W.H.: Remarks on fractional derivatives. Appl. Math. Comput. 187, 777–784 (2007)
Yu, S.M.: A new type of chaotic generator. Acta Phys. Sin. 53, 4111–4119 (2004)
Petráš, I.: Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. Higher Education Press, Beijing (2011)
Ishteva, M.: Properties and applications of the Caputo fractional operator. Msc. Thesis, Department of Mathematics, Universität Karlsruhe (TH), Sofia, Bulgaria, (2005)
Acknowledgments
This research is supported by National Natural Science Foundation of China (No. 61573184), Jiangsu Natural Science Foundation of China (No. SBK20130033), Program for New Century Excellent Talents in University of China (No. NCET-11-0830) and Specialized Research Fund for the Doctoral Program of Higher Education (No. 20133218110013).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shao, S., Chen, M. & Yan, X. Adaptive sliding mode synchronization for a class of fractional-order chaotic systems with disturbance. Nonlinear Dyn 83, 1855–1866 (2016). https://doi.org/10.1007/s11071-015-2450-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2450-1