Abstract
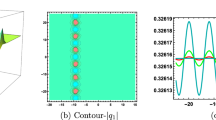
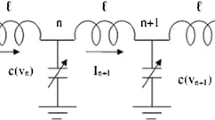
This work presents an analytical study of dynamic behaviors of solitons in the electrical transmission line. The nonlinear dynamical model that is the modified Zakharov–Kuznetsov equation with an external force is investigated. Via the Riccati equation mapping scheme, explicit twenty seven traveling wave solutions, which include periodic solutions, rational wave solution, soliton solutions as well as soliton-like solutions, are constructed for the first time.
Similar content being viewed by others
References
Duan, W.S.: Nonlinear waves propagating in the electrical transmission line. Europhys. Lett. 66, 192 (2004)
Zhen, H.L., Tian, B., Zhong, H., Jiang, Y.: Dynamic behaviors and soliton solutions of the modified Zakharov–Kuznetsov equation in the electrical transmission line. Comput. Math. Appl. 68(5), 579 (2014)
Sardar, A., Husnine, S.M., Rizvi, S.T.R., Younis, M., Ali, K.: Multiple travelling wave solutions for electrical transmission line model. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2240-9
Krishnan, E.V., Biswas, A.: Solutions to the Zakharov–Kuznetsov equation with higher order nonlinearity by mapping and ansatz methods. Phys. Wave Phenom. 18(4), 256 (2010)
Biswas, A., Zerrad, E.: 1-soliton solution of the Zakharov–Kuznetsov equation with dual-power law nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 14(9), 3574 (2009)
Bhrawy, A.H., Abdelkawy, M.A., Kumar, S., Johnson, S., Biswas, A.: Solitons and other solutions to quantum Zakharov–Kuznetsov equation in quantum magneto-plasmas. Indian J. Phys. 87(5), 455 (2013)
Biswas, A.: 1-soliton solution of the generalized Zakharov–Kuznetsov modified equal width equation. Appl. Math. Lett. 22(11), 1775 (2009)
Yang, Z.P., Zhong, W.P., Belić, M.: 2D optical rogue waves in self-focusing Kerr-type media with spatially modulated coefficients. Laser Phys. 25(8), 085402 (2015)
Wazwaz, A.M.: The extended tanh method for the Zakharov–Kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms. Commun. Nonlinear Sci. Numer. Simul. 13(6), 1039 (2008)
Wazwaz, A.M.: Nonlinear dispersive special type of the Zakharov–Kuznetsov equation ZK (n, n) with compact and noncompact structures. Appl. Math. Comput. 161(2), 577 (2005)
Wazwaz, A.M.: Solitary waves solutions for extended forms of quantum Zakharov–Kuznetsov equations. Phys. Scr. 85(2), 025006 (2012)
Wang, G.W., Xu, T.Z., Johnson, S., Biswas, A.: Solitons and Lie group analysis to an extended quantum Zakharov–Kuznetsov equation. Astrophys. Space Sci. 349(1), 317 (2014)
Ebadi, G., Mojaver, A., Milovic, D., Johnson, S., Biswas, A.: Solitons and other solutions to the quantum Zakharov–Kuznetsov equation. Astrophys. Space Sci. 341(2), 507 (2012)
Qu, Q.X., Tian, B., Liu, W.J., Sun, K., Wang, P., Jiang, Y., Qin, B.: Soliton solutions and interactions of the Zakharov–Kuznetsov equation in the electron–positron-ion plasmas. Eur. Phys. J. D 61(3), 709 (2011)
Triki, H., Yildirim, A., Hayat, T., Aldossary, O.M., Biswas, A.: Topological and non-topological soliton solutions of the Bretherton equation. Proc. Rom. Acad. Ser. A 13(2), 103 (2012)
Triki, H., Crutcher, S., Yildirim, A., Hayat, T., Aldossary, O.M., Biswas, A.: Bright and dark solitons of the modified complex Ginzburg Landau equation with parabolic and dual-power law nonlinearity. Rom. Rep. Phys. 64(2), 367 (2012)
Biswas, A.: 1-Soliton solution of the K (m, n) equation with generalized evolution and time-dependent damping and dispersion. Comput. Math. Appl. 59(8), 2536 (2010)
Biswas, A., Zony, C., Zerrad, E.: Soliton perturbation theory for the quadratic nonlinear Klein–Gordon equation. Appl. Math. Comput. 203(1), 153 (2008)
Ebadi, G., Fard, N.Y., Bhrawy, A.H., Kumar, S., Triki, H., Yildirim, A., Biswas, A.: Solitons and other solutions to the (3+1)-dimensional extended Kadomtsev–Petviashvili equation with power law nonlinearity. Rom. Rep. Phys. 65(1), 27 (2013)
Biswas, A., Milovic, D., Ranasinghe, A.: Solitary waves of Boussinesq equation in a power law media. Commun. Nonlinear Sci. Numer. Simul. 14(11), 3738 (2009)
Bhrawy, A.H., Abdelkawy, M.A., Biswas, A.: Cnoidal and snoidal wave solutions to coupled nonlinear wave equations by the extended Jacobi’s elliptic function method. Commun. Nonlinear Sci. Numer. Simul. 18(4), 915 (2013)
Bhrawy, A.H., Biswas, A., Javidi, M., Ma, W.X., Pinar, Z., Yildirim, A.: New solutions for (1+1)-dimensional and (2+1)-dimensional Kaup–Kupershmidt equations. Results Math. 63(1–2), 675 (2013)
Bhrawy, A.H., Abdelkawy, M.A., Biswas, A.: Topological solitons and cnoidal waves to a few nonlinear wave equations in theoretical physics. Indian J. Phys. 87(11), 1125 (2013)
Bhrawy, A.H., Abdelkawy, M.A., Kumar, S., Biswas, A.: Solitons and other solutions to Kadomtsev–Petviashvili equation of B-type. Rom. J. Phys. 58(7–8), 729 (2013)
Biswas, A., Bhrawy, A.H., Abdelkawy, M.A., Alshaery, A.A., Hilal, E.M.: Symbolic computation of some nonlinear fractional differential equations. Rom. J. Phys. 59(5–6), 433 (2014)
Triki, H., Kara, A.H., Bhrawy, A.H., Biswas, A.: Soliton solution and conservation law of Gear–Grimshaw model for shallow water waves. Acta Phys. Pol. A 125(5), 1099 (2014)
Triki, H., Mirzazadeh, M., Bhrawy, A.H., Razborova, P., Biswas, A.: Solitons and other solutions to long-wave short-wave interaction equation. Rom. J. Phys. 60(1–2), 72 (2015)
Mirzazadeh, M., Eslami, M., Bhrawy, A.H., Biswas, A.: Integration of complex-valued Klein–Gordon equation in \(\Phi \)-4 field theory. Rom. J. Phys. 60(3–4), 293 (2015)
Bekir, A., Guner, O., Bhrawy, A.H., Biswas, A.: Solving nonlinear fractional differential equations using exp-function and (G’/G)-expansion methods. Rom. J. Phys. 60(3–4), 360 (2015)
Bhrawy, A.H.: An efficient Jacobi pseudospectral approximation for nonlinear complex generalized Zakharov system. Appl. Math. Comput. 247, 30 (2014)
Bhrawy, A.H., Abdelkawy, M.A.: A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J. Comput. Phys. 294, 462 (2015)
Bhrawy, A.H.: A highly accurate collocation algorithm for 1+1 and 2+1 fractional percolation equations. J. Vib. Control (2015). doi:10.1177/1077546315597815
Doha, E.H., Bhrawy, A.H., Abdelkawy, M.A., Van Gorder, R.A.: Jacobi–Gauss–Lobatto collocation method for the numerical solution of 1+1 nonlinear Schrödinger equations. J. Comput. Phys. 261, 244 (2014)
Bhrawy, A.H., Zaky, M.A.: Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 80(1–2), 101 (2015)
Zhou, Q.: Analytical solutions and modulation instability analysis to the perturbed nonlinear Schrödinger equation. J. Mod. Opt. 61(6), 500 (2014)
Zhou, Q., Yao, D., Ding, S., Zhang, Y., Chen, F., Chen, F., Liu, X.: Spatial optical solitons in fifth order and seventh order weakly nonlocal nonlinear media. Optik 124(22), 5683 (2013)
Zhou, Q.: Optical solitons in the parabolic law media with high-order dispersion. Optik 125(18), 5432 (2014)
Guo, R., Liu, Y.F., Hao, H.Q., Qi, F.H.: Coherently coupled solitons, breathers and rogue waves for polarized optical waves in an isotropic medium. Nonlinear Dyn. 80(3), 1221 (2015)
Liu, W.J., Pang, L.H., Wong, P., Lei, M., Wei, Z.Y.: Dynamic solitons for the perturbed derivative nonlinear Schrödinger equation in nonlinear optics. Laser Phys. 25(6), 065401 (2015)
Zhou, Q., Liu, L., Liu, Y., Yu, H., Yao, P., Wei, C., Zhang, H.: Exact optical solitons in metamaterials with cubic-quintic nonlinearity and third-order dispersion. Nonlinear Dyn. 80(3), 1365 (2015)
Zhu, S.D.: The generalizing Riccati equation mapping method in non-linear evolution equation: application to (2+1)-dimensional Boiti–Leon–Pempinelle equation. Chaos Solitons Fractals 37(5), 1335 (2008)
Malwe, B.H., Betchewe, G., Doka, S.Y., Kofane, T.C.: Travelling wave solutions and soliton solutions for the nonlinear transmission line using the generalized Riccati equation mapping method. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2318-4
Zhou, Q., Zhu, Q.: Optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Waves Random Complex Media 25(1), 52 (2015)
Biswas, A., Mirzazadeh, M., Savescu, M., Milovic, D., Khan, K.R., Mahmood, M.F., Belic, M.: Singular solitons in optical metamaterials by ansatz method and simplest equation approach. J. Mod. Opt. 61(19), 1550 (2014)
Kong, L.Q., Dai, C.Q.: Some discussions about variable separation of nonlinear models using Riccati equation expansion method. Nonlinear Dyn. 81(3), 1553 (2015)
Kudryashov, N.A., Dimitrova, Z.I., Kantz, H.: Application of the method of simplest equation for obtaining exact traveling-wave solutions for the extended Korteweg-de Vries equation and generalized Camassa–Holm equation. Appl. Math. Comput. 219, 7480 (2013)
Acknowledgments
This work was supported by the Program for Outstanding Young and Middle-aged Scientific and Technological Innovation Team of the Higher Education Institutions of Hubei Province of China under the Grant Number T201525.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhou, Q. Soliton and soliton-like solutions to the modified Zakharov–Kuznetsov equation in nonlinear transmission line. Nonlinear Dyn 83, 1429–1435 (2016). https://doi.org/10.1007/s11071-015-2415-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-015-2415-4