Post-critical analysis of ground resonance phenomenon: effect of stator asymmetry

Abstract

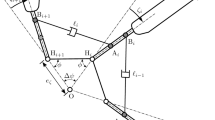
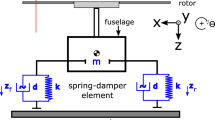
In helicopter with hinged rotor, an unstable dynamic phenomenon known as ground resonance may occur, leading to the total destruction of the aircraft. The prediction of the stability boundary has been addressed for various helicopter configurations by using different methods. However, in order to develop control strategies for this phenomenon, the post-critical behavior of the system needs to be known. In this paper, the post-critical behavior of the ground resonance instability is investigated. For this purpose, the behavior of a helicopter with four identical hinged blades is investigated and fuselage asymmetry is taken into account. It is shown that, due to fuselage asymmetry, in addition to periodic solutions the system may exhibit quasiperiodic and chaotic response.

Appendix: Energy expressions

The kinetic and potential energy expressions and the work expression of dissipative forces of the dynamical system are presented in the following. They are all written on the inertial reference frame.

• Kinetic energy:

The kinetic energy of the whole dynamical system consists in the sum of kinetic energy expression of the fuselage, $T_\mathrm{Fus}$, and the rotor head, $T_\mathrm{RH}$. The corresponding equations are given below.

$$\begin{aligned} T_\mathrm{Fus}= & {} \frac{1}{2}m_f\left( x'^2+y'^2\right) \end{aligned}$$

(45)

$$\begin{aligned} T_\mathrm{RH}= & {} \frac{1}{2}\sum _{k=1}^{N_b}\left[ I_z\phi _k'^2+m_b\left( x_{bk}'^2+y_{bk}'^2\right) \right] \end{aligned}$$

(46)

where the prime denotes differentiation with respect to the original time t.

• Potential energy:

The potential energy of the dynamic system as a whole consists in the sum of the potential energy of the fuselage, $U_\mathrm{Fus}$, and the rotor head, $U_\mathrm{RH}$. The corresponding equations are given below.

$$\begin{aligned} U_\mathrm{Fus}= & {} \frac{1}{2}K_{fx}x^2+\frac{1}{2}K_{fy}y^2 \end{aligned}$$

(47)

$$\begin{aligned} U_\mathrm{RH}= & {} \frac{1}{2}\sum _{k=1}^{N_b}K_b\phi _k^2 \end{aligned}$$

(48)

• Work of dissipative forces:

The work of dissipative forces of the dynamic system as a whole consists in the sum of the work done by dissipative forces acting on the fuselage, $\delta F_\mathrm{Fus}$, and the rotor head, $\delta F_\mathrm{RH}$. They are given below as:

$$\begin{aligned} \delta F_\mathrm{Fus}= & {} \frac{1}{2}c_{fx}x'^2+\frac{1}{2}c_{fy}y'^2 \end{aligned}$$

(49)

$$\begin{aligned} \delta F_\mathrm{RH}= & {} \frac{1}{2}\sum _{k=1}^{N_b}c_b\phi _k'^2 \end{aligned}$$

(50)