Skip to main content
SpringerLink
Log in

An adaptive fast terminal sliding mode control combined with global sliding mode scheme for tracking control of uncertain nonlinear third-order systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

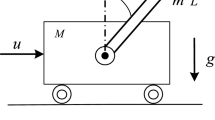
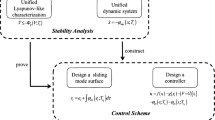
In this paper, an adaptive fast terminal sliding mode control technique combined with a global sliding mode control scheme is investigated for the tracking problem of uncertain nonlinear third-order systems. The proposed robust tracking controller is formulated based on the Lyapunov stability theory and guarantees the existence of the sliding mode around the sliding surface in a finite time. Under the uncertainty and nonlinearity effects, the reaching phase is removed and the chattering phenomenon is eliminated. This scheme guarantees robustness against nonlinear functions, parameter uncertainties and external disturbances. The derivative of the state variable is replaced by a delay term in the form of an Euler approximation of the derivative function. Furthermore, the knowledge of upper bounds of the system uncertainties is not required, which is more flexible in the real implementations. Simulation results are presented to show the effectiveness of the suggested method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Bhat, S.P., Bernstein, D.S.: Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 43, 678–682 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  2. Mobayen, S., Majd, V.J.: Robust tracking control method based on composite nonlinear feedback technique for linear systems with time-varying uncertain parameters and disturbances. Nonlinear Dyn. 70, 171–180 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Tong, S.C., Li, Y.M., Feng, G., Li, T.S.: Observer-based adaptive fuzzy backstepping dynamic surface control for a class of MIMO nonlinear systems. IEEE Trans. Syst. Man Cybern. B 41, 1124–1135 (2011)

    Article  Google Scholar 

  4. Mobayen, S.: Finite-time stabilization of a class of chaotic systems with matched and unmatched uncertainties: an LMI approach. Complex. (2014). doi:10.1002/cplx.21624

  5. Tong, S., Li, Y., Shi, P.: Observer-based adaptive fuzzy backstepping output feedback control of uncertain MIMO pure-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. 20, 771–785 (2012)

    Article  Google Scholar 

  6. Mobayen, S.: Design of LMI-based sliding mode controller with an exponential policy for a class of underactuated systems. Complex. (2014). doi:10.1002/cplx.21636

  7. Boulkroune, A., Bouzeriba, A., Hamel, S., Bouden, T.: A projective synchronization scheme based on fuzzy adaptive control for unknown multivariable chaotic systems. Nonlinear Dyn. 78(1), 433–447 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Boulkroune, A., M’saad, M.: Fuzzy adaptive observer-based projective synchronization for nonlinear systems with input nonlinearity. J. Vib. Control 18(3), 437–450 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. Mobayen, S.: Robust tracking controller for multivariable delayed systems with input saturation via composite nonlinear feedback. Nonlinear Dyn. 76, 827–838 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Boulkroune, A., Bouzeriba, A., Hamel, S., Bouden, T.: Adaptive fuzzy control-based projective synchronization of uncertain nonaffine chaotic systems. Complex. (2014). doi:10.1002/cplx.21596

  11. Sun, T., Pei, H., Pan, Y., Zhou, H., Zhang, C.: Neural network-based sliding mode adaptive control for robot manipulators. Neurocomputing 74, 2377–2384 (2011)

    Article  Google Scholar 

  12. Mobayen, S.: Finite-time tracking control of chained-form nonholonomic systems with external disturbances based on recursive terminal sliding mode method. Nonlinear Dyn. 80, 669–683 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Rao, D.V., Sinha, N.K.: A sliding mode controller for aircraft simulated entry into spin. Aerosp. Sci. Technol. 28, 154–163 (2013)

    Article  Google Scholar 

  14. Pisano, A., Usai, E.: Output-feedback control of an underwater vehicle prototype by higher-order sliding modes. Automatica 40, 1525–1531 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  15. Song, Z., Li, H., Sun, K.: Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique. ISA Trans. 53, 117–124 (2014)

    Article  Google Scholar 

  16. Allen, M., Zazzera, F.B., Scattolini, R.: Sliding mode control of a large flexible space structure. Control Eng. Pract. 8, 861–871 (2000)

    Article  Google Scholar 

  17. Mobayen, S.: An LMI-based robust controller design using global nonlinear sliding surfaces and application to chaotic systems. Nonlinear Dyn. 79, 1075–1084 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hsu, C.F., Lee, B.K.: FPGA-based adaptive PID control of a DC motor driver via sliding-mode approach. Expert Syst. Appl. 38, 11866–11872 (2011)

    Article  MathSciNet  Google Scholar 

  19. Ouassaid, M., Maaroufi, M., Cherkaoui, M.: Observer-based nonlinear control of power system using sliding mode control strategy. Electr. Power Syst. Res. 84, 135–143 (2012)

  20. Mobayen, S., Javadi, S.: Disturbance observer and finite-time tracker design of disturbed third-order nonholonomic systems using terminal sliding mode. J. Vib. Control (2015). doi:10.1177/1077546315576611

  21. Mobayen, S.: An LMI-based robust tracker for uncertain linear systems with multiple time-varying delays using optimal composite nonlinear feedback technique. Nonlinear Dyn. 80, 917–927 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Mobayen, S.: Fast terminal sliding mode tracking of non-holonomic systems with exponential decay rate. IET Control Theory Appl. (2015). doi:10.1049/iet-cta.2014.1118

  23. Mobayen, S.: An adaptive chattering-free PID sliding mode control based on dynamic sliding manifolds for a class of uncertain nonlinear systems. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2137-7

  24. Mobayen, S.: Finite-time robust-tracking and model-following controller for uncertain dynamical systems. J. Vib. Control. (2014). doi:10.1177/1077546314538991

  25. Mobayen, S.: Design of LMI-based global sliding mode controller for uncertain nonlinear systems with application to Genesio’s chaotic system. Complex. (2014). doi:10.1002/cplx.21545

  26. Mobayen, S., Majd, V.J., Sojoodi, M.: An LMI-based composite nonlinear feedback terminal sliding-mode controller design for disturbed MIMO systems. Math. Comput. Simul. 85, 1–10 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  27. Chiang, M.H.: The velocity control of an electro-hydraulic displacement-controlled system using adaptive fuzzy controller with self-tuning fuzzy sliding mode compensation. Asian J. Control 13, 492–504 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Li, L., Song, G., Ou, J.: Adaptive fuzzy sliding mode based active vibration control of a smart beam with mass uncertainty. Struct. Control Health Monit. 18, 40–52 (2011)

    Google Scholar 

  29. Zhu, M., Li, Y.: Decentralized adaptive fuzzy sliding mode control for reconfigurable modular manipulators. Int. J. Robust Nonlinear Control 20, 472–488 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  30. Bessa, W.M., Paula, A.S., Savi, M.A.: Adaptive fuzzy sliding mode control of a chaotic pendulum with noisy signals. ZAMM J. Appl. Math. Mech. 94, 256–263 (2014)

    Article  MathSciNet  Google Scholar 

  31. Ning, X.L., Tan, P., Huang, D.Y., Zhou, F.L.: Application of adaptive fuzzy sliding mode control to a seismically excited highway bridge. Struct. Control Health Monit. 16, 639–656 (2009)

    Article  Google Scholar 

  32. Pai, M.C.: Robust tracking and model following for uncertain time-delay systems with input nonlinearity. Complex. (2014). doi:10.1002/cplx.21578

  33. Roopaei, M., Sahraei, B.R., Lin, T.C.: Adaptive sliding mode control in a novel class of chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 15, 4158–4170 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Mondal, S., Mahanta, C.: Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty. ISA Trans. 52, 335–341 (2013)

    Article  Google Scholar 

  35. Pukdeboon, C., Siricharuanun, P.: Nonsingular terminal sliding mode based finite-time control for spacecraft attitude tracking. Int. J. Control Autom. Syst. 12, 530–540 (2014)

    Article  Google Scholar 

  36. Yang, J., Li, S., Su, J., Yu, X.: Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 49, 2287–2291 (2013)

    Article  MathSciNet  Google Scholar 

  37. Yang, L., Yang, J.: Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 21, 1865–1879 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  38. Yu, X., Man, Z.: Fast terminal sliding mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 49, 261–264 (2002)

    Article  MathSciNet  Google Scholar 

  39. Mobayen, S., Yazdanpanah, M.J., Majd, V.J.: A finite time tracker for nonholonomic systems using recursive singularity-free FTSM. In: 2011 American Control Conference, pp. 1720–1725, San Francisco, CA (2011)

  40. Qi, L., Shi, H.: Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control. Neurocomputing 115, 23–30 (2013)

    Article  Google Scholar 

  41. Mobayen, S.: Fast terminal sliding mode controller design for nonlinear second-order systems with time-varying uncertainties. Complex. (2014). doi:10.1002/cplx.21600

  42. Cao, Q., Li, S., Zhao, D.: Adaptive motion/force control of constrained manipulators using a new fast terminal sliding mode. Int. J. Comput. Appl. Technol. 49, 150–156 (2014)

    Article  Google Scholar 

  43. Zheng, J., Wang, H., Man, Z., Jin, J., Fu, M.: Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode. IEEE/ASME Trans. Mechatron. (2014). doi:10.1109/TMECH.2014.2352647

  44. Lu, Y.S., Chiu, C.W., Chen, J.S.: Time-varying sliding mode control for finite-time convergence. Nonlinear Dyn. 92, 257–268 (2010)

    Google Scholar 

  45. Tai, T.L., Lu, Y.S.: Global sliding mode control with chatter alleviation for robust eigenvalue assignment. J. Syst. Control Eng. 220, 573–584 (2006)

    Google Scholar 

  46. Cong, B.L., Chen, Z., Liu, X.D.: On adaptive sliding mode control without switching gain overestimation. Int. J. Robust Nonlinear Control 24, 515–531 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  47. Wu, M., Chen, J.S.: A discrete-time global quasi-sliding mode control scheme with bounded external disturbance rejection. Asian J. Control 16, 1839–1848 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  48. Yang, C., Ke, Z., Lei, D.: Research on global fast terminal sliding mode guidance law. Comput. Meas. Control 2013(2), 391–393 (2013)

    Google Scholar 

  49. Weifeng, Y., Juntao, F., Yuzheng, Y., Shixi, H.: Adaptive global fast terminal sliding mode control of MEMS gyroscope. In: 2013 32nd Chinese Control Conference, pp. 3135–3140, Xi’an, China (2013)

  50. Bartoszewicz, A., Nowacka, A.: Sliding-mode control of the third-order system subject to velocity, acceleration and input signal constraints. Int. J. Adapt. Control Signal Process. 21, 779–794 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  51. Moulay, E., Peruquetti, W.: Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 323, 1430–1443 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  52. Isidori, A.: Nonlinear Control Systems—An Introduction, 2nd edn. Springer, New York (1989)

    Book  MATH  Google Scholar 

  53. Yang, Y., Zhou, C., Jia, X.: Robust adaptive fuzzy control and its application to ship roll stabilization. Inf. Sci. 142, 177–194 (2002)

    Article  MATH  Google Scholar 

  54. Ilchmann, A., Sangwin, C.J.: Output feedback stabilisation of minimum phase systems by delays. Syst. Control Lett. 52, 233–245 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  55. Huang, Y.J., Kuo, T.C., Chang, S.H.: Adaptive sliding-mode control for nonlinear systems with uncertain parameters. IEEE Trans. Syst. Man Cybern. 38(2), 534–539 (2008)

    Article  Google Scholar 

  56. Qin, H., Ma, J., Jin, W.Y., Wang, C.N.: Dynamics of electric activities in neuron and neurons of network induced by autapses. Sci. China Technol. Sci. 57(5), 936–946 (2014)

    Article  MathSciNet  Google Scholar 

  57. Ma, J., Qin, H., Song, X., Chu, R.: Pattern selection in neuronal network driven by electric autapses with diversity in time delays. Int. J. Mod. Phys. B 29(1), 1450239 (2015)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Electrical Engineering Department, University of Zanjan, P. O. Box 38791–45371, Zanjan, Iran

    Saleh Mobayen

Authors
  1. Saleh Mobayen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saleh Mobayen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mobayen, S. An adaptive fast terminal sliding mode control combined with global sliding mode scheme for tracking control of uncertain nonlinear third-order systems. Nonlinear Dyn 82, 599–610 (2015). https://doi.org/10.1007/s11071-015-2180-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2180-4

Keywords

Search

Navigation