State-space realization of a describing function

Abstract

The describing function is a powerful tool for characterizing nonlinear dynamical systems in the frequency domain. In some cases, it is the only available description of a nonlinear operator characterizing a certain subcomponent of the system. This paper presents a methodology to provide a state-space realization of one given describing function, in order to allow the study of the system in the time domain as well. The realization is based on Hammerstein models and Fourier–Bessel series. It can be embedded in time domain simulations of complex configurations with many nonlinear elements interacting, accurately describing the nonlinear saturation of the system. The technique is applied to an example application in the field of combustion instability, featuring self-excited thermoacoustic oscillations. We benchmark the performance of the tool comparing the results with a frequency domain analysis of the same system, obtaining good agreement between the two formulations.

Appendix: Describing function calculation

In this appendix, we evaluate the describing function (defined by (1)) of the saturation function $\mathcal {N}$. We will prove here the more general result for an input with structure

$$\begin{aligned} u(t)=A_1\cos (\omega t +\varphi _1) + A_2\cos (\omega t+\varphi _2) \end{aligned}$$

(34)

to the function $\mathcal {N}$, as opposed to the case under consideration in this article introduced in (1) where $u(t)=A\cos (\omega t)$. In particular, the input described by (34) describes the contribution of two modes, oscillating at the same frequency, instead of a single sinusoidal input $A\cos (\omega t+\varphi )$. The motivation to cover this more general case is to make this framework usable in rotationally symmetric annular combustors featuring azimuthal modes. In that case, each burner is subject to the combined input of two thermoacoustic modes, depending on the amplitudes $A_1$ and $A_2$ of the two modes at that location, and on their phases $\varphi _1,\varphi _2$. Once the result for the input (34) is obtained, it will be sufficient to set $A_1=A$, $\varphi _1=\varphi _2=A_2=0$ to obtain the special case of the single-input response used in this article, as presented at the end of the appendix.

We proceed by rewriting $u$ as

$$\begin{aligned}&u=a\cos (\omega t)+b\sin (\omega t) \end{aligned}$$

(35)

by introducing the constants

$$\begin{aligned}&{\left\{ \begin{array}{ll} &{}a\equiv A_1\cos \varphi _1+A_2\cos \varphi _2\\ &{}b\equiv -A_1\sin \varphi _1-A_2\sin \varphi _2 \end{array}\right. } \end{aligned}$$

(36)

Notice that $a,b$ do not depend on the time variable $t$. We study the averaging integral in the definition (1) of describing function for the operator $\mathcal {N}$, and we will later divide by the amplitude $A$ to recover the full expression. In other words, for the time being we study the product $N(A,\omega )A$. We substitute in the product Eq. (35) and change the time variable:

$$\begin{aligned} \frac{1}{\pi }\int _0^{2\pi }\mathcal {N}\left( a\cos t \!+\! b\sin t\right) \left( \cos t \!+\!i\sin t\right) {\hbox {d}}t\!=\!f_c\!+\!if_s \end{aligned}$$

(37)

We substitute the expression for $\mathcal {N}$ from (17):

$$\begin{aligned} f_{c}&=\frac{1}{\pi }\int _0^{2\pi }q^{\text {erf}}_{\mu ,\kappa }(a\cos t+b\sin t)\cos t {\hbox {d}}t\nonumber \\&+\sum _{n=1}^N \frac{c_n}{\pi }\int _0^{2\pi }J_1(\hat{u}_n (a\cos t+b\sin t))\cos t {\hbox {d}}t\nonumber \\&\equiv f^{\text {erf}}_{c}+\sum _{n=1}^Nc_n f^{b,n}_{c} \end{aligned}$$

(38a)

$$\begin{aligned} f_{s}&=\frac{1}{\pi }\int _0^{2\pi }q^{\text {erf}}_{\mu ,\kappa }(a\cos t+b\sin t)\sin t {\hbox {d}}t\nonumber \\&+\sum _{n=1}^N \frac{c_n}{\pi }\int _0^{2\pi }J_1(\hat{u}_n (a\cos t+b\sin t))\sin t {\hbox {d}}t\nonumber \\&\equiv f^{\text {erf}}_{s}+\sum _{n=1}^Nc_n f^{b,n}_{s} \end{aligned}$$

(38b)

We study first the integrals $f^{\text {erf}}_{c}$ and $f^{\text {erf}}_{s}$ due to the error function in Sect. 4.1 and then each of the $N$ integrals $f^{b,n}_{c}$ and $f^{b,n}_{s}$ of the Fourier–Bessel series in Sect. 4.2. We put together the expressions and discuss them in Sect. 4.3.

1.1 Averaging the error function

We substitute the definition of $q_{\mu ,\kappa }^{\text {erf}}$ from (18) into the expression of $f_{c}^{\text {erf}}$ and $f_{s}^{\text {erf}}$ in (38). We obtain

$$\begin{aligned} f_{c}^{\text {erf}}&=\frac{\kappa }{\pi }\int _0^{2\pi }\text {erf}\left( \frac{\sqrt{\pi } \mu }{2\kappa }(a\cos t+b\sin t)\right) \cos t d t \end{aligned}$$

(39a)

$$\begin{aligned} f_{s}^{\text {erf}}&=\frac{\kappa }{\pi }\int _0^{2\pi }\text {erf}\left( \frac{\sqrt{\pi } \mu }{2\kappa }(a\cos t+b\sin t)\right) \sin t d t \end{aligned}$$

(39b)

For conciseness, we introduce the constant

$$\begin{aligned} k=\sqrt{\frac{\pi }{8}}\frac{\mu }{\kappa }, \end{aligned}$$

(40)

so that the argument of the $\text {erf}$ function is $\sqrt{2}k(a\cos t+b\sin t)$. This leads to neater expressions in the following. We proceed by expressing the argument of the exponential function as

$$\begin{aligned} a\cos t+b\sin t=R\sin (t+\psi ), \end{aligned}$$

(41)

where $R$ and $\psi$ are defined as

$$\begin{aligned} R\equiv&\sqrt{a^2+b^2} \end{aligned}$$

(42a)

$$\begin{aligned} \psi \equiv&\arg (b+ia) \end{aligned}$$

(42b)

The two integrals (39) become

$$\begin{aligned} f_{c}^{\text {erf}}&=\frac{\kappa }{\pi }\int _0^{2\pi }\text {erf}\left( \sqrt{2}kR\sin ( t+\psi )\right) \cos t d t \end{aligned}$$

(43a)

$$\begin{aligned} f_{s}^{\text {erf}}&=\frac{\kappa }{\pi }\int _0^{2\pi }\text {erf}\left( \sqrt{2}kR\sin ( t+\psi )\right) \sin t d t \end{aligned}$$

(43b)

We exploit the fact that the $\text {erf}$ function is defined as an integral itself and apply integration by parts to (43a):

$$\begin{aligned} f_{c}&^{\text {erf}}=\frac{\kappa }{\pi }\left[ \text {erf}\left( \sqrt{2} kR\sin ( t+\psi )\right) \sin t\right] _0^{2\pi }\nonumber \\&\qquad -\frac{\kappa }{\pi }\frac{2}{\sqrt{\pi }}\sqrt{2}k\int _0^{2\pi }e^{-2k^2R^2\sin ^2( t+\psi )}\nonumber \\ {}&\qquad \times R\cos ( t+\psi )\sin t d t \end{aligned}$$

(44)

The first term trivially vanishes. In the second, $2/\sqrt{\pi }$ is the factor present in the definition (18) of the $\text {erf}$ function, and $\sqrt{2}k$ comes from the chain rule of the derivative of $\text {erf}$ with respect to $t$, together with the term $R\cos ( t+\psi )$ inside the integral. Substituting the definition of $k$ from (40) only at its first occurrence into the second term, we can simplify:

$$\begin{aligned} \frac{\kappa }{\pi }\frac{2}{\sqrt{\pi }}\sqrt{2}k=\frac{\mu }{\pi } \end{aligned}$$

(45)

We now apply a change of integration variable $t\rightarrow \chi -\psi$ to the integral (44), and because the integrand is periodic in $t$ and then in $\chi$, we keep the same limits of integration in the new variable.

$$\begin{aligned} f_{c}^{\text {erf}}=-\frac{\mu }{\pi }R\int _0^{2\pi }e^{-2k^2R^2\sin ^2\chi }\cos \chi \sin (\chi -\psi ) {\text{ d }}\chi \end{aligned}$$

(46)

We then expand the trigonometric term $\sin (\chi -\psi )$ and take the sum out of the integral. We obtain

$$\begin{aligned} f_{c}^{\text {erf}}=&-\mu R\left[ +E_{sc}\cos \psi -E_{cc}\sin \psi \right] \end{aligned}$$

(47a)

$$\begin{aligned} f_{s}^{\text {erf}}=&-\mu R\left[ -E_{sc}\sin \psi -E_{cc}\cos \psi \right] \end{aligned}$$

(47b)

where we introduced the integrals

$$\begin{aligned} E_{sc}\equiv & {} \frac{1}{\pi }\int _0^{2\pi }e^{-2 k^2 R^2 \sin ^2\chi }\cos \chi \sin \chi d\chi =0 \end{aligned}$$

(48a)

$$\begin{aligned} E_{cc}\equiv & {} \frac{1}{\pi }\int _0^{2\pi }e^{-2 k^2 R^2 \sin ^2\chi }\cos ^2\chi {\text{ d }}\chi \nonumber \\= & {} \frac{2}{\pi }\int _0^{\pi }e^{-2 k^2 R^2 \sin ^2\chi }\cos ^2\chi {\text{ d }}\chi \end{aligned}$$

(48b)

The first integral (48a) is zero since its integrand is odd. In (48b), we exploited the fact that the integrand has period $\pi$. We then use power reduction formulas on the terms $\sin ^2\chi$ and $\cos ^2\chi$:

$$\begin{aligned} E_{cc}= & {} \frac{2}{\pi }\int _0^{\pi }e^{-k^2 R^2 (1-\cos 2\chi ) }\frac{1+\cos 2\chi }{2} {\text{ d }}\chi \nonumber \\= & {} \frac{1}{2\pi }\int _0^{2\pi }e^{-k^2 R^2 (1-\cos t) }(1+\cos t){\hbox {d}}t \end{aligned}$$

(49)

The integrand in (49) has period $2\pi$ and is an even function of $t$, so:

$$\begin{aligned} E_{cc}= & {} \frac{1}{\pi }\int _0^{\pi }e^{-k^2 R^2+k^2 R^2 \cos t }(1+\cos t) {\hbox {d}}t\nonumber \\= & {} e^{-k^2 R^2}\left( \frac{1}{\pi }\int _0^{\pi }e^{k^2 R^2 \cos t } {\hbox {d}}t\right. \nonumber \\&\left. +\frac{1}{\pi }\int _0^{\pi }e^{k^2 R^2 \cos t }\cos t {\hbox {d}}t\right) \nonumber \\= & {} e^{-k^2 R^2} \left( I_0(k^2 R^2)+I_1(k^2 R^2)\right) \end{aligned}$$

(50)

In (50), $I_0(x)$ and $I_1(x)$ are the modified Bessel functions of the first kind of the zero order and first order, respectively. We first substitute (50,48a) in (47), and then we substitute $R\sin \psi =a$ and $R\cos \psi =b$. We obtain:

$$\begin{aligned} f_{c}^{\text {erf}}= & {} af_{nl}^{\text {erf}}(kR) \end{aligned}$$

(51a)

$$\begin{aligned} f_{2}^{\text {erf}}= & {} bf_{nl}^{\text {erf}}(kR) \end{aligned}$$

(51b)

with

$$\begin{aligned} f_{nl}^{\text {erf}}(kR)\equiv \mu e^{-k^2R^2} \left( I_0(k^2R^2)+I_1(k^2R^2)\right) \end{aligned}$$

(52)

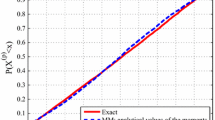
acting as a gain, as it multiplies the linear term in (51) and depends on the amplitude of oscillation. The two analytical expressions (51) have been compared with the numerical integration of (38) and its counterpart for a few values of $\mu ,\kappa ,a,b$, and lead to relative errors of the order of machine precision, thus confirming their validity.

1.2 Averaging Bessel functions

The $n$-th term of $f_{c}^{b,n}$ and of $f_{s}^{b,n}$ in (38) are, respectively,

$$\begin{aligned} f_{c}^{b,n}\equiv & {} \frac{1}{\pi }\int _0^{2\pi }J_1(2u_n a\cos t+2u_nb\sin t)\cos t d t\nonumber \\ \end{aligned}$$

(53a)

$$\begin{aligned} f_{s}^{b,n}\equiv & {} \frac{1}{\pi }\int _0^{2\pi }J_1(2u_n a\cos t+2u_nb\sin t)\sin t d t\nonumber \\ \end{aligned}$$

(53b)

where we introduced $u_n\equiv \hat{u}_n/2$. We define $\hat{f}_j^{b,n}=f_{c}^{b,n}+if_{s}^{b,n}$ and apply the substitution

$$\begin{aligned} z=e^{i t},\,\sin t=\frac{1}{2i}\left( 1-\frac{1}{z}\right) ,\,\cos t=\frac{1}{2}\left( 1+\frac{1}{z}\right) \end{aligned}$$

(54)

We obtain

$$\begin{aligned} \hat{f}_j^{b,n}=\frac{1}{\pi }\int _0^{2\pi }J_1\left( u_n (a-ib)z+u_n(a+ib)\frac{1}{z}\right) z d t \end{aligned}$$

(55)

We now change the line integral into a contour integral in the complex plane on the circle $|z|=1$. From (54), we have that $d t=dz/iz$, and

$$\begin{aligned} \hat{f}_j^{b,n}=\frac{1}{\pi i}\oint _{|z|=1} J_1\left( u_n (a-ib)z+u_n(a+ib)\frac{1}{z}\right) dz \end{aligned}$$

(56)

The Bessel function $J_1(z)$ is an entire function, so the only singularity of $\hat{f}_j^{b,n}(z)$ is at the origin and is of the essential type. We can then apply the residue theorem,

$$\begin{aligned} \hat{f}_j^{b,n}&=\frac{1}{\pi i}\,2\pi i\text{ Res }\left[ J_1\left( u_n (a-ib)z+u_n(a+ib)\frac{1}{z}\right) \right] _{z=0}\nonumber \\&=2\text{ Res }\left[ G(z)\right] _{z=0} \end{aligned}$$

(57)

We expand the Bessel function in $G(z)$ with its Laurent series:

$$\begin{aligned} G(z)=\sum _{m=0}\frac{(-1)^mu_n^{1+2m}}{m!(m+1)!}\left( \frac{(a-ib)z+(a+ib)/z}{2}\right) ^{1+2m} \end{aligned}$$

(58)

We substitute the binomial expansion of the power of the sum

$$\begin{aligned}&\left( \frac{(a-ib)z+(a+ib)/z}{2}\right) ^{1+2m}\nonumber \\&\quad =\frac{1}{2^{1+2m}}\sum _{k=0}^{1+2m}z^{k-(2m+1-k)}\left( {\begin{array}{c}1+2m\\ k\end{array}}\right) \nonumber \\ {}&\qquad \times (a-ib)^k(a+ib)^{1+2m-k} \end{aligned}$$

(59)

The residue in (58) is the sum of the coefficients of the term $1/z$. Therefore, in the sum (59), we retain only the term with $k-(2m+1-k)=-1$, from which follows $k=m$. This term of (59) is:

$$\begin{aligned}&\frac{1}{2^{1+2m}}z^{-1}\left( {\begin{array}{c}1+2m\\ m\end{array}}\right) (a-ib)^{m}(a+ib)^{m+1}\nonumber \\&=\frac{a+ib}{2}\frac{1}{2^{2m}}z^{-1}\frac{(2m+1)!}{m!(m+1)!}(a^2+b^2)^{m} \end{aligned}$$

(60)

Equation (57) evaluates to

$$\begin{aligned} \hat{f}_j^{b,n}=&(a+ib)\sum _{m=0}^\infty \frac{(-1)^m(2m+1)!u_n^{1+2m}}{(m!(m+1)!)^2}\left( \frac{R}{2}\right) ^{2m} \end{aligned}$$

with $R=\sqrt{a^2+b^2}$. This series converges to

$$\begin{aligned} \hat{f}_j^{b,n}=&(a+i b)\frac{2 J_0\left( u_n\sqrt{a^2+b^2}\right) J_1\left( u_n\sqrt{a^2+b^2}\right) }{\sqrt{a^2+b^2}} \end{aligned}$$

(61)

The two forcing terms (53) can be evaluated as the real and imaginary parts of (61):

$$\begin{aligned} f_{c}^{b,n}= & {} a f_{nl}^{b,n}(R) \end{aligned}$$

(62a)

$$\begin{aligned} f_{s}^{b,n}= & {} b f_{nl}^{b,n}(R) \end{aligned}$$

(62b)

where we introduced

$$\begin{aligned} f_{nl}^{b,n}(R)\equiv 2\frac{J_0\left( u_nR\right) J_1\left( u_nR\right) }{R} \end{aligned}$$

(63)

1.3 Final expression

The final expression of $f_{c}$ and of $f_{s}$ is obtained by substituting (51) and (62) into (38):

$$\begin{aligned} f_{c}(a,b)= & {} a\left( f_{nl}^{\text {erf}}(kR)+\sum _{n=1}^{N}c_nf_{nl}^{b,n}(R)\right) = a f_{nl}(R)\nonumber \\ \end{aligned}$$

(64a)

$$\begin{aligned} f_{s}(a,b)= & {} b\left( f_{nl}^{\text {erf}}(kR)+\sum _{n=1}^{N}c_nf_{nl}^{b,n}(R)\right) = b f_{nl}(R)\nonumber \\ \end{aligned}$$

(64b)

with $u_n=\hat{u}_n/2$, the constant $k=\mu /\kappa \sqrt{\pi /8}$ as defined in (40), the value of $R$ is defined in (42a) and

$$\begin{aligned} f_{nl}(R)\equiv f_{nl}^{\text {erf}}(kR)+\sum _{n=1}^{N}c_nf_{nl}^{b,n}(R) \end{aligned}$$

(65)

where $f_{nl}^{\text {erf}}$ and $f_{nl}^{b,n}$ have been defined, respectively, in (52) and (63). The two terms $f_{c}$ and $f_{s}$ in (64) are symmetric with respect to $a,b$, since we have $f_c(a,b)=f_s(b,a)$.

By exploiting the fact that $\lim _{R\rightarrow 0}J_1(R)/R=1/2$, and then substituting (21), we observe that

$$\begin{aligned} \lim _{R\rightarrow 0}f_{nl}(R)=\mu +\sum _{j=0}^Nc_n u_n=\mu +\frac{1}{2}\sum _{j=0}^Nc_n\hat{u}_n\equiv \beta \end{aligned}$$

(66)

where we substituted the property (21) in the last passage.

It can be proved that the first derivative at zero is

$$\begin{aligned} \lim _{R\rightarrow 0}\frac{\partial f_{nl}}{\partial R}(R)=0, \end{aligned}$$

(67)

meaning that $f_{nl}$ is constant at first order in $R$.

In the case of the input described by a single sinusoid $A\cos (\omega t)$, it is sufficient to set $A_1=A$, $\varphi _1=\varphi _2=A_2=0$. In the definitions (36), this leads to $a=A,b=0$, and the substitution of these in (64) leads to

$$\begin{aligned} f_{c}(a,b)= & {} A\left( f_{nl}^{\text {erf}}(kA)+\sum _{n=1}^{N}c_nf_{nl}^{b,n}(A)\right) \nonumber \\= & {} A f_{nl}(A) \end{aligned}$$

(68a)

$$\begin{aligned} f_{s}(a,b)= & {} 0 \end{aligned}$$

(68b)

The component in quadrature with the input signal $u$ is zero, and $N(A)$ is real valued. Substituting (68) in (37), because (37) is equal to $N(A,\omega )A$, we obtain

$$\begin{aligned} N(A,\omega )=&f_{nl}(A) \end{aligned}$$

(69)

with $f_{nl}$ matching the RHS of (22).