Skip to main content

Advertisement

SpringerLink
Log in

Synchronization of reaction–diffusion neural networks with time-varying delays via stochastic sampled-data controller

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

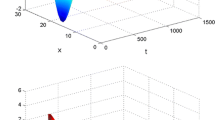
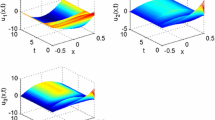
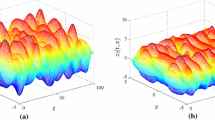
This paper discusses the synchronization problem for a class of reaction–diffusion neural networks with Dirichlet boundary conditions. Unlike other studies, a sampled-data controller with stochastic sampling is designed in order to synchronize the concerned neural networks with reaction–diffusion terms and time-varying delays, where \(m\) sampling periods are considered whose occurrence probabilities are given constants and satisfy the Bernoulli distribution. A novel discontinuous Lyapunov–Krasovskii functional with triple integral terms is introduced based on the extended Wirtinger’s inequality. Using Jensen’s inequality and reciprocally convex technique in deriving the upper bound for the derivative of the Lyapunov–Krasovskii functional, some new synchronization criteria are obtained in terms of linear matrix inequalities. Numerical examples are provided in order to show the effectiveness of the proposed theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Young, S., Scott, P., Nasrabadi, N.: Object recognition using multilayer Hopfield neural network. IEEE Trans. Image Process. 6, 357–372 (1997)

    Article  Google Scholar 

  2. Atencia, M., Joya, G., Sandoval, F.: Dynamical analysis of continuous higher order Hopfield neural networks for combinatorial optimization. Neural Comput. 17, 1802–1819 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  3. Hopfield, J.: Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 81, 3088–3092 (1984)

    Article  Google Scholar 

  4. Diressche, P., Zou, X.: Global attractivity in delayed Hopfield neural network models. SIAM J. Appl. Math. 58, 1878–1890 (1998)

    Article  MathSciNet  Google Scholar 

  5. Grassi, G., Mascolo, S.: Synchronizing high dimensional chaotic systems via eigenvalue placement in application to cellular neural networks. Int. J. Bifur. Chaos 9, 705–711 (1999)

    Article  MATH  Google Scholar 

  6. Ortin, S., Gutierrez, J.M., Pesquera, L., Vasquez, H.: Nonlinear dynamic extraction for time-delay systems using modular neural networks synchronization and prediction. Phys. A 351, 133–141 (2005)

    Article  Google Scholar 

  7. Sanchez, E.N., Ricalde, L.J.: Chaos control and synchronization with input saturation via recurrent neural networks. Neural Netw. 16, 711–717 (2003)

    Article  Google Scholar 

  8. Zhu, Q., Cao, J.: pth moment exponential synchronization for stochastic delayed Cohen–Grossberg neural networks with Markovian switching. Nonlinear Dyn. 67, 829–845 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  9. Zhu, Q., Cao, J.: Adaptive synchronization under almost every initial data for stochastic neural networks with time-varying delays and distributed delays. Commun. Nonlinear Sci. Numer. Simulat. 16, 2139–2159 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  10. Cheng, C., Liao, T., Hwang, C.: Exponential synchronization of a class of chaotic neural networks. Chaos Solitons Fract. 24, 197–206 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  11. Marcus, C.M., Westervelt, R.M.: Stability of analog neural networks with delay. Phys. Rev. A 39, 347–359 (1989)

    Article  MathSciNet  Google Scholar 

  12. Civalleri, P., Gilli, M., Pandolfi, L.: On stability of cellular neural networks with delay. IEEE Trans. Circuits Syst. I 40(40), 157–165 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  13. Cheng, C.J., Liao, T.L., Yang, J.J., Hwang, C.C.: Exponential synchronization of a class of neural networks with time-varying delays. IEEE Trans. Syst. Man Cybern. Part-B 36, 209–215 (2006)

    Article  Google Scholar 

  14. Cui, B.T., Lou, X.Y.: Synchronization of chaotic recurrent neural networks with time-varying delays using nonlinear feedback control. Choas Solitons Fract. 39, 288–294 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  15. Gao, X., Zhong, S., Gao, F.: Exponential synchronization of neural networks with time-varying delays. Nonlinear Anal. 71, 2003–2011 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  16. Wang, L., Ding, W., Chen, D.: Synchronization schemes of a class of fuzzy cellular neural networks based on adaptive control. Phys. Lett. A. 74, 1440–1449 (2010)

    Article  Google Scholar 

  17. Lu, J.: Robust global exponential stability for interval reaction–diffusion Hopfield neural networks with distributed delays. IEEE Trans. Circuits Syst. II Expr. Briefs 54, 1115–1119 (2007)

    Article  Google Scholar 

  18. Lu, J., Lu, L.: Global exponential stability and periodicity of reaction–diffusion recurrent neural networks with distributed delays and Dirichlet boundary conditions. Chaos Solitons Fract. 39, 1538–1549 (2009)

    Article  MATH  Google Scholar 

  19. Li, X., Cao, J.: Delay-independent exponential stability of stochastic Cohen–Grossberg neural networks with time-varying delays and reaction–diffusion terms. Nonlinear Dyn. 50, 363–371 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  20. Lu, J.: Global exponential stability and periodicity of reaction–diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fract. 35, 116–125 (2008)

    Article  MATH  Google Scholar 

  21. Wang, J., Lu, J.: Global exponential stability of fuzzy cellular neural networks with delays and reaction–diffusion terms. Chaos Solitons Fract. 38, 878–885 (2008)

    Article  MATH  Google Scholar 

  22. Hu, C., Jiang, H., Teng, Z.: Impulsive control and synchronization for delayed neural networks with reaction–diffusion terms. IEEE Trans. Neural Netw. 21, 67–81 (2010)

    Article  Google Scholar 

  23. Kashima, K., Ogawa, T., Sakurai, T.: Feedback stabilization of non-uniform spatial pattern in reaction-diffusion systems. American Control Conference (ACC), Washington, DC, USA, June 17–19 (2013)

  24. Zhao, A., Xie, C.: Stabilization of coupled linear plant and reaction–diffusion process. J. Franklin Inst. 351, 857–877 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  25. Wang, K., Teng, Z., Jiang, H.: Adaptive synchronization in an array of linearly coupled neural networks with reaction–diffusion terms and time-delays. Commun. Nonlinear Sci. Numer. Simul. 17, 3866–3875 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  26. Yang, X., Cao, J., Yang, Z.: Synchronization of coupled reaction–diffusion neural networks with time-varying delays via pinning-impulsive controller. SIAM J. Control Optim. 51, 3486–3510 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  27. Wu, Z.-G., Park, J.H., Su, H., Chu, J.: Discontinuous Lyapunov functional approach to synchronization of time-delay neural networks using sampled-data. Nonlinear Dyn. 69, 2021–2030 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  28. Lam, H.: Stabilization of nonlinear systems using sampled-data output-feedback fuzzy controller based on polynomial-fuzzy-model-based control approach. IEEE Trans. Syst. Man Cybern. Part B Cybern. 42, 258–267 (2012)

    Article  Google Scholar 

  29. Zhu, X., Wang, Y.: Stabilization for sampled-data neural-network-based control systems. IEEE Trans. Syst. Man Cybern. Part B Cybern. 41, 210–221 (2011)

    Article  MATH  Google Scholar 

  30. Gan, Q., Liang, Y.: Synchronization of chaotic neural networks with time-delay in the leakage term and parametric uncertainties based on sampled-data control. J. Franklin Inst. 349, 1955–1971 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  31. Jeeva Sathya Theesar, S., Santo, B., Balasubramaniam, P.: Synchronization of chaotic systems under sampled-data control. Nonlinear Dyn. 70, 1977–1987 (2012)

    Article  MATH  Google Scholar 

  32. Krishnasamy, R., Balasubramaniam, P.: Stabilisation analysis for switched neutral systems based on sampled-data control. Int. J. Syst. Sci. doi:10.1080/00207721.2013.871368

  33. Wu, Z., Shi, P., Su, H., Chu, J.: Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled-data. IEEE Trans. Cybern. 43, 1796–1806 (2013)

    Article  Google Scholar 

  34. Lakshmanan, S., Park, J.H., Rakkiyappan, R., Jung, Y.: State estimator for neural networks with sampled data using discontinuous Lyapunov functional approach. Nonlinear Dyn. 73, 509–520 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  35. Tahara, S., Fujii, T., Yokoyama, T.: Variable sampling quasi multirate deadbeat control method for single phase PWM inverter in low carrier frequency, pp. 804–809. In PCC. Power Conversion Conference (2007)

  36. Hu, B., Michel, A.N.: Stability analysis of digital feedback control systems with time-varying sampling periods. Automatica 36, 897–905 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  37. Sala, A.: Computer control under time-varying sampling period: an LMI gridding approach. Automatica 41, 2077–2082 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  38. Gao, H., Wu, J., Shi, P.: Robust sampled-data \(H_{\infty }\) control with stochastic sampling. Automatica 45, 1729–1736 (2009)

  39. Lee, T., Park, J., Lee, S., Kwon, O.: Robust synchronization of chaotic systems with randomly occurring uncertainties via stochastic sampled-data control. Int. J. Control 86, 107–119 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  40. Kwon, O., Lee, S., Park, J., Cha, E.: New approaches on stability criteria for neural networks with interval time-varying delays. Appl. Math. Comput. 218, 9953–9964 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  41. Tian, J., Zhong, S.: Improved delay-dependent stability criterion for neural networks with time-varying delay. Appl. Math. Comput. 217, 10278–10288 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  42. Park, P., Ko, J., Jeong, C.: Reciprocally convex approach to stability of systems with time-varying delays. Automatica 7, 235–238 (2011)

    Article  MathSciNet  Google Scholar 

  43. Wang, Y., Cao, J.: Synchronization of a class of delayed neural networks with reaction–diffusion terms. Phys. Lett. A 369, 201–211 (2007)

  44. Lou, X., Cui, B.: Asymptotic synchronization of a class of neural networks with reaction–diffusion terms and time-varying delays. Comput. Math. Appl. 52, 897–904 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  45. Balasubramaniam, P., Chandran, R., Jeeva Sathya Theesar, S.: Synchronization of chaotic nonlinear continuous neural networks with time-varying delay. Cogn. Neurodyn. 5, 361–371 (2011)

  46. Balasubramaniam, P., Vembarasan, V.: Synchronization of recurrent neural networks with mixed time-delays via output coupling with delayed feedback. Nonlinear Dyn. 70, 677–691 (2012)

  47. Kalpana, M., Balasubramaniam, P.: Stochastic asymptotical synchronization of chaotic Markovian jumping fuzzy cellular neural networks with mixed delays and the Wiener process based on sampled-data control. Chin. Phys. B 22, 078401 (2013)

    Article  Google Scholar 

Download references

Acknowledgments

The work of the first author was supported by NBHM Research Project; Quanxin Zhu’s work was jointly supported by the National Natural Science Foundation of China (61374080), the Natural Science Foundation of Zhejiang Province (LY12F03010), the Natural Science Foundation of Ningbo (2012A610032), and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Author information

Authors and Affiliations

  1. Department of Mathematics, Bharathiar University, Coimbatore, 641 046, Tamilnadu, India

    R. Rakkiyappan & S. Dharani

  2. School of Mathematical Sciences, Institute of Finance and Statistics, Nanjing Normal University, Nanjing, 210023, Jiangsu, China

    Quanxin Zhu

Authors
  1. R. Rakkiyappan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Dharani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Quanxin Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quanxin Zhu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rakkiyappan, R., Dharani, S. & Zhu, Q. Synchronization of reaction–diffusion neural networks with time-varying delays via stochastic sampled-data controller. Nonlinear Dyn 79, 485–500 (2015). https://doi.org/10.1007/s11071-014-1681-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1681-x

Keywords

Search

Navigation