Abstract
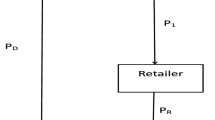
In the oligopoly e-commerce market, the oligarch retailers sell products through traditional channel, while others through both network and traditional channel in order to obtain greater profits. Instead of discussing classic Bertrand game model, which past studies have done, we considered dual-channel retailer who makes price decision through both in network channel and traditional channel. This paper used the bifurcation theory of dynamical system, considering dual-channel retailer who makes delay decision. We performed a numerical simulation on system with different conditions, and some complex phenomenons occured, such as bifurcation and chaos. The results showed that adopting price delay decision in tradition channel would make the system more stable. While, adopting price delay decision in network channel makes the system less stable. When the market is in chaotic state, the using of delay decision would have an effect on the system stability in either traditional or network channels. The system become stable from chaos and would return to chaotic again with the increasing of weight in past period. Some interesting phenomenons happened when dual-channel retailer adopted delay decision in both channels. The superposition of delay decision would make the system more complex. At last, we measured the system’s performance by using profit index. We analyzed the profits of different oligarchs when the system is in different states. When the system is in chaos, the total profits of the oligarchs are obviously less than that in a stable state. Adopting delay decision is a way to avoid profit loss when system is in chaotic period, but this requires the retailer has rich operational experience. That is because adopting delayed decision may not always enhance the competitive strength of oligarchs.











Similar content being viewed by others
References
Balasubramanian, S.: Mail versus mall: a strategic analysis of competition between direct marketers and conventional retailers. Mark. Sci. 17(3), 181–195 (1998)
Geyskens, I., Gielens, K., Dekimpe, M.G.: The market valuation of Internet channel additions. J. Mark. 66(2), 102–119 (2002)
Khouja, M., Park, S., Cai, G.G.: Channel selection and pricing in the presence of retail-captive consumers. Int. J. Prod. Econ. 125(1), 84–95 (2010)
Cournot, A.: Recherches sur les Principes Mathematiques de la Theorie des Richesses. Hachette, Paris (1938)
Bertrand, J.: Review of Theorie mathematique de la richesse sociale and of Recherches sur les principles mathematiques de la theorie des richesses. J. des Savants. 67, 499–508 (1883)
Theocharis, R.D.: On the stability of the Cournot solution on the oligopoly problem. Rev. Econ. Stud. 27(2), 133–134 (1960)
Puu, T.: Complex dynamics with three oligopolists. Chaos Solitons Fract. 7(12), 2075–2081 (1996)
Puu, T.: On the stability of Cournot equilibrium when the number of competitors increases. J. Econ. Behav. Organ. 66(3–4), 445–456 (2008)
Puu, T., Panchuk, A.: Oligopoly and stability. Chaos Solitons Fract. 41(5), 2505–2516 (2009)
Rand, D.: Exotic phenomena in games and Duopoly models. J. Math. Econ. 5(2), 173–184 (1978)
Agiza, H.N., Elsadany, A.A.: Nonlinear dynamics in the Cournot duopoly game with heterogeneous players. Phys. A Statis. Mech. Appl. 320, 512–524 (2003)
Agiza, H.N., Elsadany, A.A.: Chaotic dynamics in nonlinear duopoly game with heterogeneous players. Appl. Math. Comput. 149(3), 843–860 (2004)
Baumol, W., Quandt, R.E.: Rules of thumb and optimally imperfect decisions. Am. Econ. Rev. 54, 23–46 (1964)
Bonanno, G., Zeeman, C.: Limited knowledge of demand and oligopoly equilibria. J. Econ. Theory 35(2), 276–283 (1985)
Flam, S.D.: Oligopolistic Competition: From Stability to Chaos, pp. 232–237. Springer, Berlin (1993)
Bischi, G., Lamantia, F.: Nonlinear duopoly games with positive cost externalities due to spillover effects. Chaos Solitons Fract. 13(4), 701–721 (2002)
Bischi, G., Tramontana, F.: Three-dimensional discrete-time Lotka–Volterra models with an application to industrial clusters. Commun. Nonlinear Sci. Numer. Simul. 15(10), 3000–3014 (2010)
Chen, Z.Q., Ip, W.H., Chan, C.Y., Yung, K.L.: Two-level chaos-based video cryptosystem on H.263 codec. Nonlinear Dyn. 62, 647–664 (2010)
Chen, Z.Q., Yang, Y., Yuan, Z.Z.: A single three-wing or four-wing chaotic attractor generated from a three dimensional smooth quadratic autonomous system. Chaos Solitons Fract. 38, 1187–1196 (2008)
Li, T., Ma, J.: The complex dynamics of R&D competition models of three oligarchs with heterogeneous players. Nonlinear Dyn. 74, 45–54 (2013)
Li, T., Ma, J.: Complexity analysis of dual-channel game model with different managers business objectives. Commun. Nonlinear Sci. Numer. Simul. 20, 199–208 (2015)
Gao, X., Zhong, W., Mei, S.: Nonlinear Cournot oligopoly games with isoelastic demand function: the effects of different behavior rules. Commun. Nonlinear Sci. Numer. Simul. 17(12), 5249–5255 (2012)
Ma, J., Ji, W.: Complexity of repeated game model in electric power triopoly. Chaos Solitons Fract. 40(4), 1735–1740 (2009)
Zhang, J., Ma, J.: Research on the price game model for four oligarchs with different decision rules and its chaos control. Nonlinear Dyn. 70(1), 323–334 (2012)
Elsadany, A.A.: Dynamics of a delayed duopoly game with bounded rationality. Math. Comput. Model. 52, 1479–1489 (2010)
Bischi, G., Naimzadaz, A.: Global analysis of a dynamic Duopoly game with bounded rationality. Adv. Dyn. Games Appl. 5, 361–385 (2000)
Li, C., Peng, J., Huang, Q.: Controlling synchronization of chaos and hyperchaos systems. J. Northeast Norm. Univ. Nat. Sci. 33(3), 43–47 (2001)
Acknowledgments
The authors would like to thank the reviewers for their careful reading and some pertinent suggestions. The research was supported by the National Natural Science Foundation of China (No. 61273231), Doctoral Fund of Ministry of Education of China (Grant No. 20130032110073) and supported by Tianjin University Innovation Fund.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, T., Ma, J. Complexity analysis of the dual-channel supply chain model with delay decision. Nonlinear Dyn 78, 2617–2626 (2014). https://doi.org/10.1007/s11071-014-1613-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-014-1613-9