Skip to main content
SpringerLink
Log in

Frequency response of primary resonance of electrostatically actuated CNT cantilevers

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

An Erratum to this article was published on 28 August 2014

Abstract

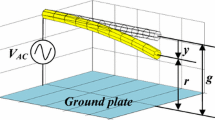
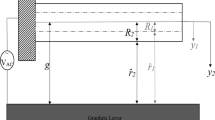
This paper deals with electrostatically actuated carbon nanotube (CNT) cantilever over a parallel ground plate. Three forces act on the CNTs cantilever, namely electrostatic, van der Waals, and damping. The van der Waals force is significant for values of 50 nm or less of the gap between the CNT and the ground plate. As both forces electrostatic and van der Waals are nonlinear, and the CNTs electrostatic actuation is given by AC voltage, the CNT undergoes nonlinear parametric dynamics. The methods of multiple scales and reduced order model (ROM) are used to investigate the system under soft AC near half natural frequency of the CNT and weak nonlinearities. The frequency–amplitude response and damping, voltage, and van der Waals effects on the response are reported. It is showed that only five terms ROM predicts and accurately predicts the pull-in instability and the saddle-node bifurcation, respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Iijima, S.: Helical micro-tubules of graphitic carbon. Nature 345, 56 (1991)

    Article  Google Scholar 

  2. Ren, X., Chen, C., Nagatsu, M., Wang, X.: Carbon nanotubes as adsorbents in environmental pollution management: a review. Chem. Eng. J. 170, 395–410 (2011)

    Article  Google Scholar 

  3. Groven, L.J., Puszynski, J.A.: Combustion synthesis and characterization of nickel aluminide-carbon nanotube composite. Chem. Eng. J. 183, 515–525 (2012)

    Article  Google Scholar 

  4. Li, K., Wang, W., Cao, D.: Metal (Pd, Pt)-decorated carbon nanotubes for CO and NO sensing. Sens. Actuators B Chem. 159, 171–177 (2011)

    Article  Google Scholar 

  5. Kumar, B., Castro, M., Feller, J.F.: Poly (lactic acid)-multi-wall carbon nanotube conductive biopolymer Nano composite vapor sensors. Sens. Actuators B Chem. 161, 621–628 (2012)

    Article  Google Scholar 

  6. Cheung, W., Pontoriero, F., Taratula, O., Chen, A., He, H.: DNA and carbon nanotubes as medicine. Adv. Drug. Deliv. Rev. 62, 633–649 (2010)

    Article  Google Scholar 

  7. Peretz, S., Regev, O.: Carbon nanotubes as nanocarriers in medicine. Curr. Opin. Colloid Interface Sci. 17, 360–368 (2012)

    Article  Google Scholar 

  8. Meng, L., Zhang, X., Lu, Q., Fei, Z., Dyson, P.J.: Single walled carbon nanotubes as drug delivery vehicles: targeting doxorubicin to tumors. Biomaterials 33, 1689–1698 (2012)

    Article  Google Scholar 

  9. Orynbayeva, Z., Singhal, R., Vitol, E.A., Schrlau, M.G., Papazoglou, E., Friedman, G., Gogotsi, Y.: Physiological validation of the cell health upon probing with carbon nanotube endoscope and its benefit for single-cell interrogation, Nanomedicine: Nanotechnology. Biol. Med. 8, 590–598 (2012)

  10. Aydogdu, M., Filiz, S.: Modeling carbon nanotube-based mass sensors using axial vibration and nonlocal elasticity. Physica E 43, 1229–1234 (2011)

    Article  Google Scholar 

  11. Pathangi, H., Cherman, V., Khaled, A., Soree, B., Groeseneken, G., Witvrouw, A.: Towards CMOS-compatible single-walled carbon nanotube resonators. Microelectron. Eng. 107, 219–222 (2013)

    Article  Google Scholar 

  12. Lassagne, B., Bachtold, A.: Carbon nanotube electromechanical resonator for ultrasensitive mass/force sensing. Comptes Rendus Phys. 11, 355–361 (2010)

    Article  Google Scholar 

  13. Sung, M., Paek, S., Ahn, S., Lee, J.H.: A study of carbon-nanotube-based nanoelectromechanical resonators tuned by shear strain. Comput. Mater. Sci. 51, 360–364 (2012)

    Article  Google Scholar 

  14. Lu, X., Hu, Z.: Mechanical property evaluation of single-walled carbon nanotubes by finite element modeling. Compos. B 43, 1902–1913 (2012)

    Article  Google Scholar 

  15. Georgantzinos, S.K., Anifantis, N.K.: Vibration analysis of multi-walled carbon nanotubes using a spring-mass based finite element model. Comput. Mater. Sci. 47, 168–177 (2009)

    Article  Google Scholar 

  16. Nayfeh, A.H., Younis, M.I., Abdel-Rahman, E.M.: Dynamic pull-in phenomenon in MEMS resonators. Nonlinear Dyn. 48, 153–163 (2007)

    Article  MATH  Google Scholar 

  17. Kacem, N., Hentz, S., Pinto, D., Reig, B., Nguyen, V.: Nonlinear dynamics of Nano mechanical beam resonators: improving the performance of NEMS-based sensors. Nanotechnology 20, 275501 (2009)

    Article  Google Scholar 

  18. Mestrom, R.M.C., Fey, R.H.B., van Beek, J.T.M., Phan, K.L., Nijmeijer, H.: Modeling the dynamics of a MEMs resonator: simulations and experiments. Sens. Actuators A 142, 306–315 (2008)

    Article  Google Scholar 

  19. Conley, W.G., Yu, L., Nellis, M.R., Raman, A., Krousgrill, C.M., Mohammadi, S., Rhoads, J.F.: The nonlinear dynamics of electrostatically-actuated single-walled carbon nanotube. In: Proceedings of the RASD 2010 \(10^{{\rm th}}\) International conference 12–14 July, Southampton (2010)

  20. Ouakad, H., Younis, M.: Natural frequencies and mode shapes of initially curved carbon nanotube resonators under electric excitation. J. Sound Vib. 330, 3182–3195 (2011)

    Article  Google Scholar 

  21. Ouakad, H.M., Younis, M.I.: Dynamic response of slacked single-walled carbon nanotube resonators. Nonlinear Dyn. 67, 1419–1436 (2012)

    Article  MathSciNet  Google Scholar 

  22. Ouakad, H.M., Younis, M.I.: Nonlinear dynamics of electrically actuated carbon nanotube resonators. J. Comput. Nonlinear Dyn. 5(011009), 1–13 (2010)

    Google Scholar 

  23. Pratiher, B.: Tuning the nonlinear behavior of resonance MEMs sensors actuated electrically. Procedia Eng. 47, 9–12 (2012)

  24. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1979)

    MATH  Google Scholar 

  25. Jia, X.L., Yang, J., Kitipornchai, S., Lim, C.W.: Resonance frequency response of geometrically nonlinear micro-switches under electrical actuation. J. Sound Vib. 331, 3397–3411 (2012)

  26. Caruntu, D.I., Knecht, M.W.: On nonlinear response near-half natural frequency of electrostatically actuated micro resonators. Int. J. Struct. Stab. Dyn. 11(4), 641–672 (2011)

    Article  Google Scholar 

  27. Vogl, G.W., Nayfeh, A.H.: Primary resonance excitation of electrically actuated clamped circular plates. Nonlinear Dyn. 47, 181–192 (2007)

    Article  MATH  Google Scholar 

  28. Kim, I.K., Lee, S.I.: Theoretical investigation of nonlinear resonances in a carbon nanotube cantilever with a tip-mass under electrostatic excitation. J. Appl. Phys. 114, 104303 (2013)

    Article  Google Scholar 

  29. Nayfeh, A.H., Ouakad, H.M., Najar, F., Choura, S., Abdel-Rahman, E.M.: Nonlinear dynamics of a resonant gas sensor. Nonlinear Dyn. 59, 607–618 (2010)

    Article  MATH  Google Scholar 

  30. Crespo da Silva, M.R.M., Glynn, C.C.: Nonlinear flexural-flexural-torsional dynamics of inextensional beams. I. Equations of motion. Mech. Based Des. Struct. Mach. 6(4), 437–448 (1978)

  31. Luongo, A., Rega, G., Vestroni, F.: On nonlinear dynamics of planar shear indeformable beams. J. Appl. Mech. 53, 619 (1986)

    Article  MATH  Google Scholar 

  32. Luongo, A., D, Zulli: Mathematical Models of Beams and Cables. Iste - Wiley, West Sussex (2013)

    Book  Google Scholar 

  33. Hornstein, S., Gottlieb, O.: Nonlinear dynamics, stability and control of the scan process in noncontacting atomic force microscopy. Nonlinear Dyn. 54, 93–122 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rega, G., Settimi, V.: Bifurcation, response scenarios and dynamic integrity in a single-mode model of noncontact atomic force microscopy. Nonlinear Dyn. 73, 101–123 (2013)

  35. Dequenes, M., Rotkin, S.V., Aluru, N.R.: Calculation of pull-in voltages for carbon-nanotube-based nanoelectromechanical switches. Nanotechnology 13, 120–131 (2002)

  36. Girifalco, L.A., Hodak, M., Lee, R.S.: Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 62(13), 104–110 (2000)

    Google Scholar 

  37. Caruntu, D.I., Martinez, I., Knecht, M.W.: ROM analysis of frequency response of AC near half natural frequency electrostatically actuated MEMS cantilevers. J. Comput. Nonlinear Dyn. 8, 031011–1–031011–6 (2013)

    Google Scholar 

  38. Caruntu, D.I., Martinez, I., Taylor, K.N.: Voltage–amplitude response of alternating current near half natural frequency electrostatically actuated MEMS resonators. Mech. Res. Commun. 52, 25–31 (2013)

    Article  Google Scholar 

  39. Batra, R., Porfiri, M., Spinello, D.: Reduced-order models for microelectromechanical rectangular and circular plates incorporating the Casimir effect. Int. J. Solids Struct. 45, 3558–3583 (2008)

    Article  MATH  Google Scholar 

  40. Papanikos, P., Nikolopoulos, D.D., Tserpes, K.I.: Equivalent beams for carbon nanotubes. Comput. Mater. Sci. 43, 345–352 (2008)

  41. Hsu, J.-C., Chang, R.-P., Chang, W.-J.: Resonance frequency of chiral single-walled carbon nanotubes using Timoshenko beam theory. Phys. Lett. A 372, 2757–2759 (2008)

    Article  MATH  Google Scholar 

  42. Gibson, R.F., Ayorinde, E.O., Wen, Y.-F.: Vibrations of carbon nanotubes and their composites: a review. Compos. Sci. Technol. 67, 1–28 (2007)

    Article  Google Scholar 

  43. Wang, Q., Varadan, V.K.: Vibration of carbon nanotubes studied using nonlocal continuum mechanics. Smart Mater. Struct. 15, 659–666 (2006)

    Article  Google Scholar 

  44. Rasekh, M., Khadem, S.E.: Nonlinear vibration and stability analysis of axially loaded embedded carbon nanotubes conveying fluid. J. Phys. D: Appl. Phys. 42, 135112 (2009)

    Article  Google Scholar 

  45. Rafiee, M., Mareishi, S., Mohammadi: An investigation on primary resonance phenomena of elastic medium based single walled carbon nanotubes. Mech. Res. Commun. 44, 51–56 (2012)

  46. Hajnayeb, A., Khadem, S.E.: Nonlinear vibration and stability analysis of a double-walled carbon nanotube under electrostatic actuation. J. Sound Vib. 331, 2443–2456 (2012)

    Article  Google Scholar 

  47. Caruntu, D.I., Taylor, K.: Bifurcation type change of AC electrostatically actuated MEMS resonators due to DC voltage. Shock Vib. vol. 2014, Article ID 542023, 9 pages (2014). http://dx.doi.org/10.1155/2014/542023

  48. Caruntu, D.I., Martinez, I.: Reduced order model of parametric resonance of electrostatically actuated MEMS cantilever resonators. Int. J. Non-Linear Mech. (2014). http://dx.doi.org/10.1016/j.ijnonlinmec.2014.02.007

  49. Bender, C.M., Orszag, S.A.: Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill Book Company, New York (1978)

    MATH  Google Scholar 

  50. Ouakad, H.M., Younis, M.I.: Nonlinear dynamics of electrically actuated carbon nanotube resonators. J. Comput. Nonlinear Dyn. 5(1), 011009 (2010)

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Science Foundation under DMR Grant # 0934157 (PREM-The University of Texas Pan American/University of Minnesota - Science and Engineering of Polymeric and Nanoparticle-based Materials for Electronic and Structural Applications).

Author information

Authors and Affiliations

  1. Mechanical Engineering Department, University of Texas-Pan American, Edinburg, TX, 78539, USA

    Dumitru I. Caruntu & Le Luo

Authors
  1. Dumitru I. Caruntu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Le Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dumitru I. Caruntu.

Additional information

Starting fall 2015, University of Texas-Pan American becomes University of Texas-Rio Grande Valley (RGV).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Caruntu, D.I., Luo, L. Frequency response of primary resonance of electrostatically actuated CNT cantilevers. Nonlinear Dyn 78, 1827–1837 (2014). https://doi.org/10.1007/s11071-014-1537-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1537-4

Keywords

Search

Navigation