Skip to main content
SpringerLink
Log in

Analysis of the stability and Hopf bifurcation of money supply delay in complex macroeconomic models

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

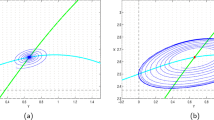
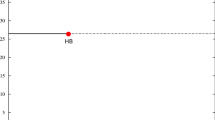
Considering the macroeconomic model of money supply, this paper carries out the corresponding extension of the complex dynamics to macroeconomic model with time delays. By setting the parameters, we discuss the effect of delay variation on system stability and Hopf bifurcation. Results of analysis show that the stability of time-delay systems has important significance with the length of time delay. When time delay is short, the stable point of the system is still in a stable region; when time delay is long, the equilibrium point of the system will go into chaos, and the Hopf bifurcation will appear in certain conditions. In this paper, using the normal form theory and center manifold theorem, the periodic solutions of the system are obtained, and the related numerical analysis are also given; this paper has important innovation-theoretical value and acts as important actual application in macroeconomic system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Fanti, L.: Fiscal policy and tax collection lags: stability, cycles and chaos. Riv. Int. Sci. Econ. Commer. 51(3), 341–365 (2004)

    Google Scholar 

  2. Gao, Q., Ma, J.: Chaos and Hopf bifurcation of a finance system. Nonlinear Dyn. 58, 209–216 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  3. Li, Z., Tang, Y., Hussein, S.: Stability and Hopf bifurcation for a delay competition diffusion system. Chaos Solitons Fractals 14, 1201–1225 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  4. Yan, X., Li, W.: Hopf bifurcation and global periodic solutions in a delayed predator–prey system. Appl. Math. Comput. 177, 427–445 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. Szydlowski, M., Krawiec, A.: The stability problem in the Kaldor–Kalecki business cycle model. Chaos Solitons Fractals 25, 229–305 (2005)

    Article  MathSciNet  Google Scholar 

  6. Ma, J., Gao, Q.: Analysis and simulation of chaotic character of business cycle model. DCDIS Ser. B 14(s5), 310–315 (2007)

    MathSciNet  Google Scholar 

  7. Ma, J., Sun, T., Wang, Z.: Hopf bifurcation and complexity of a kind of economic system. Int. J. Nonlinear Sci. Numer. Simul. 8(3), 347–352 (2007)

    Article  Google Scholar 

  8. Chen, Z.Q., Yang, Y., Yuan, Z.Z.: A single three-wing or four-wing chaotic attractor generated from a three-dimensional smooth quadratic autonomous system. Chaos Solitons Fractals 38, 1187–1196 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  9. Ma, J., Zhang, Q., Gao, Q.: Stability of a three-species symbiosis model with delays. Nonlinear Dyn. 67, 567–572 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  10. Sun, Z., Ma, J.: Complexity of triopoly price game in Chinese cold rolled steel market. Nonlinear Dyn. 67, 2001–2008 (2012)

    Article  MathSciNet  Google Scholar 

  11. Zhang, J., Ma, J.: Research on the price game and the application of delayed decision in oligopoly insurance market. Nonlinear Dyn. 70, 2327–2341 (2012)

    Article  Google Scholar 

  12. Chen, Y.: Stability and Hopf bifurcation analysis in a three-level food chain system with delay. Chaos Solitons Fractals 31, 683–694 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  13. Zhang, C., Wei, J.: Stability and bifurcation analysis in a kind business cycle model with delay. Chaos Solitons Fractals 22, 883–896 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  14. Cai, J.: Hopf bifurcation in the IS-LM business cycle model with time delay. Electron. J. Differ. Equ. 15, 1–6 (2005)

    Google Scholar 

  15. De Cesare, L., Sportelli, M.: A dynamic IS-LM model with delayed taxation revenues. Chaos Solitons Fractals 25, 233–244 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  16. Milhaela, N., Dumitru, O., Constantin, C.: Hopf bifurcation in a dynamic IS-LM model with time delay. Chaos Solitons Fractals 34, 519–530 (2007)

    Article  MathSciNet  Google Scholar 

  17. Hassard, B., Kazarinoff, D., Wan, Y.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)

    MATH  Google Scholar 

  18. Chen, Z.Q., Ip, W.H., Chan, C.Y., Yung, K.L.: Two-level chaos-based video cryptosystem on H.263 codec. Nonlinear Dyn. 62, 647–664 (2010)

    Article  Google Scholar 

  19. Ruan, S., Wei, J.: On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal. 10, 863–874 (2003)

    MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by The National Nature Science Foundation of China (grant No. 61273231) and supported by Doctoral Fund of Ministry of Education of China (grant No. 20130032110073).

Author information

Authors and Affiliations

  1. College of Management and Economics, Tianjin University, Tianjin, 300072, China

    Junhai Ma & Hongliang Tu

  2. School of Management, China University of Mining and Technology, Xuzhou, 221116, China

    Hongliang Tu

Authors
  1. Junhai Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hongliang Tu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Junhai Ma or Hongliang Tu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ma, J., Tu, H. Analysis of the stability and Hopf bifurcation of money supply delay in complex macroeconomic models. Nonlinear Dyn 76, 497–508 (2014). https://doi.org/10.1007/s11071-013-1143-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-1143-x

Keywords

Search

Navigation