Skip to main content

Advertisement

SpringerLink
Log in

Dynamic non-linear energy absorbers based on properly stretched in-plane elastomer structures

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

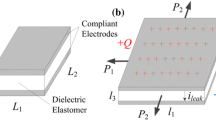
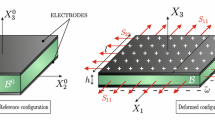
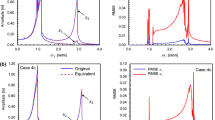
Abstract

Traditionally, elastomers are considered to be one of the best material candidates for the design of energy absorbing devices, due to their remarkable visco-elastic and extensibility material properties. This capability can be further enhanced by the design of appropriate Dielectric Elastomer Generators (DEGs). The present paper proceeds to another alternative direction, which consists of the design of appropriate elastomer structures with enhanced energy absorption capabilities, are attributed more to the appropriate non-linear design of the elastomer structure itself, than to the hyperelastic material properties of the elastomer members. For this reason, a simple chi-shaped in-plane elastic structure is considered, comprising one proof mass with four elastomer members attached to it, placed in a chi-shaped configuration, and being properly stretched. A systematic analysis is carried out, with respect to the variation of two basic structure design properties on the dynamic behavior: the orientation angle of the members and their initial pre-stress. The obtained results show that the variation of just these two basic parameters of the structure may lead to a quite rich and interesting non-linear dynamic behavior. More specifically, the traditional always-in-tension concept leads to a linear dynamic system response, even though the elastomer members are considered to have been made of a non-linear hyper-elastic material. Alternatively, a new partially-loose-member operating concept is analyzed. This concept suggests that some individual elastomer members be allowed to become loose for some period of the operating cycle, (but not all of them simultaneously), strongly enhancing the broadband energy absorbing capability of the structure itself.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Pelrine, R., Kornbluh, R., Pei, Q., Joseph, J.: High-speed electrically actuated elastomers with strain greater than 100 %. Science 287, 836–839 (2000)

    Article  Google Scholar 

  2. Pelrine, R., Kornbluh, R., Eckerle, J., Jeuck, P., Oh, S., Pei, Q., Stanford, S.: Dielectric elastomers: generator mode fundamentals and applications. Proc. SPIE 4329, 148–156 (2001)

    Article  Google Scholar 

  3. Jean-Mistral, C., Basrour, S., Chaillout, J.J.: Modelling of dielectric polymers for energy scavenging applications. Smart Mater. Struct. (2010). doi:10.1088/0964-1726/19/10/105006

    Google Scholar 

  4. Koh, S.J.A., Keplinger, C., Li, T., Bauer, S., Suo, Z.: Dielectric elastomer generators: how much energy can be converted? IEEE/ASME Trans. Mechatron. 16(1), 33–41 (2011)

    Article  Google Scholar 

  5. Baumgartner, R., Keplinger, C., Kaltseis, R., Schwödiauer, R., Bauer, S.: Dielectric elastomers: from the beginning of modern science to applications in actuators and energy harvesters. Proc. SPIE (2011). doi:10.1117/12.880289

    Google Scholar 

  6. Falcão, A.F. de O.: Wave energy utilization: a review of the technologies. Renew. Sustain. Energy Rev. 14, 899–918 (2010)

    Article  Google Scholar 

  7. Tang, L., Yang, Y., Soh, C.K.: Toward broadband vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 21, 1867–1897 (2010)

    Article  Google Scholar 

  8. Anton, S.R., Sodano, H.A.: A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. (2007). doi:10.1088/0964-1726/16/3/R01

    Google Scholar 

  9. Lallart, M., Wu, Y.C., Richard, C., Guyomar, D., Halvorsen, E.: Broadband modeling of a nonlinear technique for energy harvesting. Smart Mater. Struct. (2012). doi:10.1088/0964-1726/21/11/115006

    Google Scholar 

  10. Dalzell, P., Bonello, P.: Analysis of an energy harvesting piezoelectric beam with energy storage circuit. Smart Mater. Struct. (2012). doi:10.1088/0964-1726/21/10/105029

    Google Scholar 

  11. Seuaciuc-Osorio, T., Daqaq, M.F.: Energy harvesting under excitations of time-varying frequency. J. Sound Vib. 329, 2497–2515 (2010)

    Article  Google Scholar 

  12. Sebald, G., Kuwano, H., Guyomar, D., Ducharne, B.: Simulation of a Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. (2011). doi:10.1088/0964-1726/20/7/075022

    Google Scholar 

  13. Wang, H.Y., Shan, X.B., Xie, T.: An energy harvester combining a piezoelectric cantilever and a single degree of freedom elastic system. Univ.-Sci. A, Appl. Phys. Eng. 13(7), 526–537 (2012)

    Google Scholar 

  14. Daqaq, M.F.: On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 69, 1063–1079 (2012)

    Article  Google Scholar 

  15. Abdelkefi, A., Nayfeh, A.H., Hajj, M.R.: Enhancement of power harvesting from piezoaeroelastic systems. Nonlinear Dyn. 68, 531–541 (2012)

    Article  Google Scholar 

  16. Mann, B.P., Owens, B.A.: Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 329, 1215–1226 (2010)

    Article  Google Scholar 

  17. Ramlan, R., Brennan, M.J., Mace, B.R., Kovacic, I.: Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 59, 545–558 (2010)

    Article  MATH  Google Scholar 

  18. Quinn, D.D., Triplett, A.L., Bergman, L.A., Vakakis, A.F.: Comparing linear and essentially nonlinear vibration-based energy harvesting. J. Vib. Acoust. (2011). doi:10.1115/1.4002782

    Google Scholar 

  19. Trigona, C., Dumas, N., Latorre, L., Andò, B., Baglio, S., Nouet, P.: Exploiting benefits of a periodically-forced nonlinear oscillator for energy harvesting from ambient vibrations. Proc. Eng. 25, 819–822 (2012)

    Article  Google Scholar 

  20. Orazov, B., O’Reilly, O.M., Zhou, X.: On forced oscillations of a simple model for a novel wave energy converter. Nonlinear Dyn. 67, 1135–1146 (2012)

    Article  MathSciNet  Google Scholar 

  21. Andersen, D., Starosvetsky, Y., Vakakis, A., Bergman, L.: Dynamic instabilities in coupled oscillators induced by geometrically nonlinear damping. Nonlinear Dyn. 67, 807–827 (2012)

    Article  MathSciNet  Google Scholar 

  22. Elshurafa, A.M., Khirallah, K., Tawfik, H.H., Emira, A., Abdel Aziz, A.K.S., Sedky, S.M.: Nonlinear dynamics of spring softening and hardening in folded-MEMS comb drive resonators. J. Microelectromech. Syst. 20(4), 943–958 (2011)

    Article  Google Scholar 

  23. Papaspiridis, F.G., Antoniadis, I.A.: Dielectric elastomer actuators as elements of active vibration control systems. Adv. Sci. Technol. 61, 103–111 (2008)

    Article  Google Scholar 

  24. Antoniadis, I.A., Venetsanos, D.T., Papaspyridis, F.G.: DIESYS—dynamically non-linear dielectric elastomer energy generating synergetic structures: perspectives and challenges. Smart Mater. Struct. (2013). doi:10.1088/0964-1726/22/10/104007

    Google Scholar 

  25. Graf, C., Maas, J.: Electroactive polymer devices for active vibration damping. Proc. SPIE (2011). doi:10.1117/12.879934

    Google Scholar 

  26. Stoker, J.J.: Nonlinear Vibrations in Mechanical and Electrical Systems. Wiley, New York (1950)

    MATH  Google Scholar 

  27. Stephen, N.G.: On energy harvesting from ambient vibration. J. Sound Vib. 293, 409–425 (2006)

    Article  Google Scholar 

  28. Kalmár-Nagy, T., Balachandran, B.: Forced harmonic vibration of a Duffing oscillator with linear viscous damping. In: Kovacic, I., Brennan, M.J. (eds.) The Duffing Equation: Nonlinear Oscillators and Their Behaviour, pp. 139–173. Wiley, New York (2011)

    Chapter  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dynamics and Structures Laboratory, School of Mechanical Engineering, National Technical University of Athens, Zografos Campus, Athens, 15780, Greece

    I. A. Antoniadis, D. T. Venetsanos & F. G. Papaspyridis

Authors
  1. I. A. Antoniadis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. T. Venetsanos
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. G. Papaspyridis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. T. Venetsanos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Antoniadis, I.A., Venetsanos, D.T. & Papaspyridis, F.G. Dynamic non-linear energy absorbers based on properly stretched in-plane elastomer structures. Nonlinear Dyn 75, 367–386 (2014). https://doi.org/10.1007/s11071-013-1072-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-1072-8

Keywords

Search

Navigation