Skip to main content
SpringerLink
Log in

Limit cycles and integrability in a class of system with a high-order critical point

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

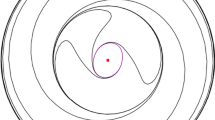
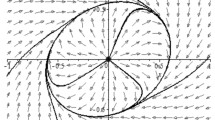
In this paper, a class of polynomial differential system with high-order critical point are investigated. The system could be changed into a system with a 3-order nilpotent critical point. Finally, an example was given, with the help of computer algebra system MATHEMATICA, the first three quasi-Lyapunov constants are deduced. As a result, sufficient and necessary conditions in order to have a center are obtained. The fact that there three small amplitude limit cycles created from the 3-order nilpotent critical point is also proved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Liu, Y., Li, J.: Some Classical Problems About Planar Vector Fields. Science Press, Beijing (2010) (in Chinese)

    Google Scholar 

  2. Álvarez, M.J., Gasull, A.: Momodromy and stability for nilpotent critical points. Int. J. Bifurc. Chaos 15, 1253–1265 (2005)

    Article  MATH  Google Scholar 

  3. Álvarez, M.J., Gasull, A.: Generating limit cycles from a nilpotent critical point via normal forms. J. Math. Anal. Appl. 318, 271–287 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  4. Zhang, Q., Liu, Y.: A cubic polynomial system with seven limit cycles at infinity. Appl. Math. Comput. 177, 319–329 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Liu, Y., Huang, W.: Seven large-amplitude limit cycles in a cubic polynomial system. Int. J. Bifurc. Chaos 16, 473–485 (2006)

    Article  MATH  Google Scholar 

  6. Zhang, Q., Liu, Y.: A quintic polynomial differential system with eleven limit cycles at the infinity. Comput. Math. Appl. 53, 1518–1526 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Zhang, Q., Gui, W., Liu, Y.: Bifurcation of limit cycles at the equator for a class of polynomial differential system. Nonlinear Anal., Real World Appl. 10, 1042–1047 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Andreev, A.F., Sadovskii, A.P., Tsikalyuk, V.A.: The center-focus problem for a system with homogeneous nonlinearities in the case of zero eigenvalues of the linear part. Differ. Equ. 39, 155–164 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Li, F.: Bifurcations of limit cycles in a quintic Lyapunov system with eleven parameters. Chaos Solitons Fractals 45, 1417–1422 (2012)

    Article  MathSciNet  Google Scholar 

  10. Li, F., Liu, Y., Wu, Y.: Center conditions and bifurcation of limit cycles at three-order nilpotent critical point in a septic Lyapunov system. Math. Comput. Simul. 81, 2595–2607 (2011)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This research is partially supported by the National Nature Science Foundation of China (11201211, 61273012) and Nature Science Foundation of Shan-dong Province (ZR2012AL04).

Author information

Authors and Affiliations

  1. School of Science, Linyi University, Linyi, 276005, Shandong, P.R. China

    Li Feng

Authors
  1. Li Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li Feng.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Feng, L. Limit cycles and integrability in a class of system with a high-order critical point. Nonlinear Dyn 73, 665–670 (2013). https://doi.org/10.1007/s11071-013-0820-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-0820-0

Keywords

Search

Navigation