Skip to main content
SpringerLink
Log in

Localized coherent structures based on variable separation solution of the (2+1)-dimensional Boiti–Leon–Pempinelli equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

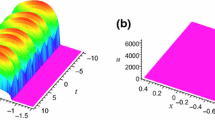
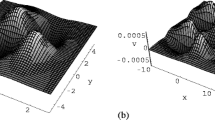
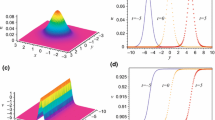
A new mapping equation (coupled Riccati equations) method is used to obtain three kinds of variable separation solutions with two arbitrary functions of the (2+1)-dimensional Boiti–Leon–Pempinelli equation. Based on the variable separation solution and by selecting appropriate functions, two type of multidromion excitations, that is, dromion lattice and multidromion solitoffs, are investigated. Moreover, we can discuss head-on collision and “chase and collision” phenomena between two multidromions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Biswas, A., Khalique, C.M.: Stationary solutions for nonlinear dispersive Schrodinger’s equation. Nonlinear Dyn. 63, 623–626 (2011)

    Article  MathSciNet  Google Scholar 

  2. Zhang, Y., Yang, S., Li, C., Ge, J.Y., Wei, W.W.: Exact solutions and Painleve analysis of a new (2+1)-dimensional generalized KdV equation. Nonlinear Dyn. (2011). doi:10.1007/s11071-011-0228-7

    Google Scholar 

  3. Zhang, S.: Exact solutions of a KdV equation with variable coefficients via Exp-function method. Nonlinear Dyn. 53, 11–17 (2008)

    Article  Google Scholar 

  4. Ye, C.E., Zhang, W.G.: New explicit solutions for (2+1)-dimensional soliton equation. Chaos Solitons Fractals 44, 1063–1069 (2011)

    Article  MathSciNet  Google Scholar 

  5. Lü, X., Tian, B., Zhang, H.Q., Xu, T., Li, H.: Generalized (2+1)-dimensional Gardner model: bilinear equations, Backlund transformation, lax representation and interaction mechanisms. Nonlinear Dyn. 67, 2279–2290 (2012)

    Article  MATH  Google Scholar 

  6. Lou, S.Y., Lu, J.Z.: Special solutions from variable separation approach: Davey–Stewartson equation. J. Phys. A, Math. Gen. 29, 4029–4215 (1996)

    MathSciNet  Google Scholar 

  7. Tang, X.Y., Lou, S.Y., Zhang, Y.: Localized excitations in (2+1)-dimensional systems. Phys. Rev. E 66, 046601 (2002)

    Article  MathSciNet  Google Scholar 

  8. Ma, S.H., Zhang, Y.L.: Fractal structures and chaotic behaviors in a (2+1)-dimensional nonlinear system. Commun. Theor. Phys. 57, 1117–1121 (2010)

    Google Scholar 

  9. Zheng, C.L., Fang, J.P., Chen, L.Q.: New variable separation excitations of a (2+1)-dimensional Broer–Kaup–Kupershmidt system obtained by an extended mapping approach. Z. Naturforsch. A 59, 912–918 (2004)

    Google Scholar 

  10. Dai, C.Q., Zhou, G.Q.: Exotic interactions between solitons of the (2+1)-dimensional asymmetric Nizhnik–Novikov–Veselov system. Chin. Phys. 16, 1201–1208 (2007).

    Article  Google Scholar 

  11. Dai, C.Q., Zhou, G.Q., Zhang, J.F.: Exotic localized structures based on variable separation solution of (2+1)-dimensional KdV equation via the extended tanh-function method. Chaos Solitons Fractals 33, 1458–1467 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  12. Yang, Z., Ma, S.H., Fang, J.P.: Chaotic solutions of (2+1)-dimensional Broek–Kaup equation with variable coefficients. Chin. Phys. B 20, 040301 (2011)

    Article  Google Scholar 

  13. Dai, C.Q., Zhang, J.F.: New types of interactions based on variable separation solutions via the general projective Riccati equation method. Rev. Math. Phys. 19, 195–221 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dai, C.Q.: Semifoldons with fusion and fision properties of (2+1)-dimensional nonlinear system. Chaos Solitons Fractals 38, 474–480 (2008)

    Article  MATH  Google Scholar 

  15. Boiti, M., Leon, J.J.P., Pempinelli, F.: Spectral transform for a two spatial dimension extension of the dispersive long wave equation. Inverse Probl. 3, 371–387 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  16. Garagash, T.I.: Modification of the Painleve test for systems of nonlinear partial differential equations. Theor. Math. Phys. 100, 1075–1081 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  17. Lu, Z.S., Zhang, H.Q.: Soliton like and multi-soliton like solutions for the Boiti–Leon–Pempinelli equation. Chaos Solitons Fractals 19, 527–531 (2004)

    Article  MathSciNet  Google Scholar 

  18. Dai, C.Q., Wang, Y.Y.: Periodic structures based on variable separation solution of the (2+1)-dimensional Boiti–Leon–Pempinelli equation. Chaos Solitons Fractals 39, 350–355 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ma, S.H., Zhang, Y.L.: Fractal structures and chaotic behaviors in a (2+1)-dimensional nonlinear system. Commun. Theor. Phys. 57, 1117–1121 (2010)

    Google Scholar 

  20. Dai, C.Q., Wang, Y.Y.: Combined wave solutions of the (2+1)-dimensional generalized Nizhnik–Novikov–Veselov system. Phys. Lett. A 372, 1810–1815 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Babaoglu, C.: Some special solutions of a generalized Davey–Stewartson system. Chaos Solitons Fractals 30, 781–790 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  22. Ma, S.H., Fang, J.P.: New exact solutions and localized excitations in a (2+1)-dimensional soliton system. Z. Naturforsch. A 64, 37–43 (2009)

    Google Scholar 

  23. Zheng, C.L., Fang, J.P., Chen, L.Q.: Soliton fission and fusion in (2+1)-Dimensional Boiti–Leon–Pempinelli system. Commun. Theor. Phys. 43, 681–687 (2005)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 11005092), the Program for Innovative Research Team of Young Teachers in Zhejiang A&F University (Grant No. 2009RC01), and the Scientific Research and Developed Fund of Zhejiang A&F University (Grant No. 2009FK42).

Author information

Authors and Affiliations

  1. School of Sciences, Zhejiang Agriculture and Forestry University, Lin’an, Zhejiang, 311300, P.R. China

    Chao-Qing Dai & Yue-Yue Wang

Authors
  1. Chao-Qing Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yue-Yue Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chao-Qing Dai.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dai, CQ., Wang, YY. Localized coherent structures based on variable separation solution of the (2+1)-dimensional Boiti–Leon–Pempinelli equation. Nonlinear Dyn 70, 189–196 (2012). https://doi.org/10.1007/s11071-012-0441-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-012-0441-z

Keywords

Search

Navigation