Skip to main content

Advertisement

SpringerLink
Log in

Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

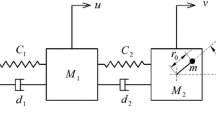
We explore the conservative and dissipative dynamics of a two-degree-of-freedom (2-DoF) system consisting of a linear oscillator and a lightweight nonlinear rotator inertially coupled to it. When the total energy of the system is large enough, the motion of the rotator is, generically, chaotic. Moreover, we show that if the damping of the rotator is sufficiently small and the damping of the linear oscillator is even smaller, then the system passes through a cascade of resonance captures (transient internal resonances) as the total energy gradually decreases. Rather unexpectedly, all these captures have the same principal frequency but correspond to different nonlinear normal modes (NNMs). In each NNM, the rotator is phase-locked into periodic motion with two frequencies. The NNMs differ by the ratio of these frequencies, which is approximately an integer for each NNM. Essentially non-integer ratios lead to incommensurate periods of ‘slow’ and ‘fast’ motions of the rotator and, thus, to its chaotic behavior between successive resonance captures. Furthermore, we show that these cascades of resonance captures lead to targeted energy transfer (TET) from the linear oscillator to the rotator, with the latter serving, in essence, as a nonlinear energy sink (NES). Since the inertially-coupled NES that we consider has no linearized natural frequency, it is capable of engaging in resonance with the linear oscillator over broad frequency and energy ranges. The results presented herein indicate that the proposed rotational NES appears to be a promising design for broadband shock mitigation and vibration energy harvesting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Gendelman, O.V.: Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators. Nonlinear Dyn. 25, 237–253 (2001)

    Article  MATH  Google Scholar 

  2. Vakakis, A.F., Gendelman, O.V.: Energy pumping in nonlinear mechanical oscillators: part II—resonance captures. J. Appl. Mech. 68, 42–48 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  3. Manevitch, L.I., Gourdon, E., Lamarque, C.H.: Towards the design of an optimal energetic sink in a strongly inhomogeneous two-degree-of-freedom system. J. Appl. Mech. 74, 1078–1086 (2007)

    Article  Google Scholar 

  4. Quinn, D.D., Gendelman, O.V., Kerschen, G., Sapsis, T.P., Bergman, L.A., Vakakis, A.F.: Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: part I. J. Sound Vib. 311, 1228–1248 (2008)

    Article  Google Scholar 

  5. Sapsis, T.P., Vakakis, A.F., Gendelman, O.V., Bergman, L.A., Kerschen, G., Quinn, D.D.: Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: part II, analytical study. J. Sound Vib. 325, 297–320 (2009)

    Article  Google Scholar 

  6. Vakakis, A.F., Gendelman, O.V., Kerschen, G., Bergman, L.A., McFarland, D.M., Lee, Y.S.: Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems, I and II. Springer, Berlin and New York (2008)

    Google Scholar 

  7. Gendelman, O.V.: Targeted energy transfer in systems with non-polynomial nonlinearity. J. Sound Vib. 315, 732–745 (2008)

    Article  Google Scholar 

  8. Gendelman, O.V., Lamarque, C.-H.: Dynamics of linear oscillator coupled to strongly nonlinear attachment with multiple states of equilibrium. Chaos Solitons Fractals 24, 501–509 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Georgiades, F., Vakakis, A.F., McFarland, D.M., Bergman, L.A.: Shock isolation through passive energy pumping caused by non-smooth nonlinearities. Int. J. Bifurc. Chaos 15(6), 1–13 (2005)

    Google Scholar 

  10. Nucera, F., Vakakis, A.F., McFarland, D.M., Bergman, L.A., Kerschen, G.: Targeted energy transfers in vibro-impact oscillators for seismic mitigation. Nonlinear Dyn. 50, 651–677 (2007)

    Article  MATH  Google Scholar 

  11. Gendelman, O.V., Sigalov, G., Manevitch, L.I., Mane, M., Vakakis, A.F., Bergman, L.A.: Dynamics of an eccentric rotational nonlinear energy sink. J. Appl. Mech. 79(1), 011012 (2012)

    Article  Google Scholar 

  12. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, Berlin and New York (1983)

    MATH  Google Scholar 

  13. Chang, Y.-H., Segur, H.: An asymptotic symmetry of the rapidly forced pendulum. Preprint, University of Colorado, Boulder, CO (1991)

  14. Greenspan, B., Holmes, P.: Repeated resonance and homoclinic bifurcation in a periodically forced family of oscillators. SIAM J. Math. Anal. 15, 69–97 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  15. Delshams, A., Seara, T.: An asymptotic expression for the splitting of separatrices of the rapidly forced pendulum. Commun. Math. Phys. 150(3), 443 (1992)

    Article  MathSciNet  Google Scholar 

  16. Shaw, S.W., Geist, B.: Tuning for performance and stability in systems of nearly tautochronic torsional vibration absorbers. J. Vib. Acoust. 132, 041005 (2010)

    Article  Google Scholar 

  17. Gendelman, O.V.: Bifurcations of nonlinear normal modes of a linear oscillator with strongly nonlinear damped attachment. Nonlinear Dyn. 37, 115–128 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Lee, Y.S., Kerschen, G., Vakakis, A.F., Panagopoulos, P., Bergman, L.A., McFarland, D.M.: Complicated dynamics of a linear oscillator with a light, essentially nonlinear attachment. Physica D 204, 41–69 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Pilipchuk, V.N., Vakakis, A.F., Azeez, M.A.F.: Sensitive dependence on initial conditions of strongly nonlinear periodic orbits of the forced pendulum. Nonlinear Dyn. 16, 223–237 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  20. Gendelman, O.V., Sigalov, G., AL-Shudeifat, M.A., Manevitch, L.I., Vakakis, A.F., Bergman, L.A.: Alternation of regular and chaotic dynamics in a simple mechanical system with nonlinear inertial coupling. Chaos (2012, in press)

  21. Holopainen, T.P., Tenhunen, A., Lantto, E., Arkkio, A.: Unbalanced magnetic pull induced by arbitrary eccentric motion of cage rotor in transient operation, part 1: analytical model. Electr. Electron. Eng. 88, 13–24 (2005)

    Article  Google Scholar 

  22. Manevitch, L.I.: Complex representation of dynamics of coupled nonlinear oscillators. In: Uvarova, L., Arinstein, A., Latyshev, A. (eds.) Mathematical Models of Non-Linear Excitations, Transfer Dynamics and Control in Condensed Systems and Other Media. Kluwer, Academic/Plenum, New York (1999)

    Google Scholar 

Download references

Acknowledgements

This work was funded in part by the (US–Israel) Binational Science Foundation (Grant 2008055), to which the authors express their gratitude.

Author information

Authors and Affiliations

  1. Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, USA

    G. Sigalov, M. A. AL-Shudeifat, A. F. Vakakis & L. A. Bergman

  2. Faculty of Mechanical Engineering, Technion—Israel Institute of Technology, Haifa, Israel

    O. V. Gendelman

  3. Institute of Chemical Physics, Russian Academy of Sciences, Moscow, Russia

    L. I. Manevitch

Authors
  1. G. Sigalov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. V. Gendelman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. A. AL-Shudeifat
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. L. I. Manevitch
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. A. F. Vakakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. L. A. Bergman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Sigalov.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sigalov, G., Gendelman, O.V., AL-Shudeifat, M.A. et al. Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink. Nonlinear Dyn 69, 1693–1704 (2012). https://doi.org/10.1007/s11071-012-0379-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-012-0379-1

Keywords

Search

Navigation