Skip to main content
SpringerLink
Log in

Order reduction and nonlinear behaviors of a continuous rotor system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

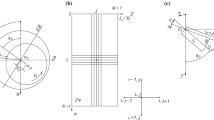
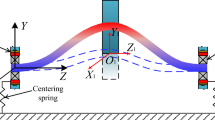
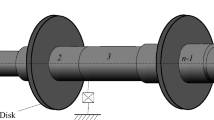
An isotropic flexible shaft, acted by nonlinear fluid-induced forces generated from oil-lubricated journal bearings and hydrodynamic seal, is considered in this paper. Dimension reductions of the rotor system were carried out by both the standard Galerkin method and the nonlinear Galerkin method. Numerical simulations provide bifurcation diagrams, spectrum cascade, orbits of the disk center and Poincaré maps, to demonstrate the dynamical behaviors of the system. The results reveal transitions, or bifurcations, of the rotor whirl from being synchronous to non-synchronous as the unstable speed is exceeded. The non-synchronous oil/seal whirl is a quasi-periodic motion. In the regime of quasi-periodic motion, the “windows” of multi-periodic motion were found. The investigation shows that the nonlinear Galerkin method has an advantage over the standard one with the same order of truncations, because the influences of higher modes are considered by the former.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Shaw, J., Shaw, S.: The effects of unbalance on oil whirl. Nonlinear Dyn. 1, 293–311 (1990)

    Article  Google Scholar 

  2. Muszynska, A.: Whirl and whip—Rotor/bearing stability problems. J. Sound Vib. 110, 443–462 (1986)

    Article  Google Scholar 

  3. Childs, D.W.: Dynamic analysis of turbulent annular seals based on Hirs’ lubrication. J. Lubr. Technol. 105, 429–439 (1983)

    Article  Google Scholar 

  4. San Andres, L.: Dynamic force and moment coefficients for short length annular seals. J. Tribol. 115, 61–70 (1993)

    Article  Google Scholar 

  5. Muszynska, A.: Improvements in lightly loaded rotor/bearing and rotor/seal models. ASME J. Vib. Acoust. 110, 129–136 (1988)

    Google Scholar 

  6. Muszynska, A., Bently, D.E.: Frequency-swept rotating input perturbation techniques and identification of the fluid force models in rotor/bearing/seal systems and fluid handling machines. J. Sound Vib. 143, 103–124 (1990)

    Article  Google Scholar 

  7. Muszynska, A., Bently, D.E.: Anti-swirl arrangements prevent rotor/seal instability. ASME J. Vib. Acoust. 111, 156–162 (1989)

    Google Scholar 

  8. Ding, Q., Cooper, J.E., Leung, A.Y.T.: Hopf bifurcation analysis of a rotor/seal system. J. Sound Vib. 252, 817–833 (2002)

    Article  Google Scholar 

  9. Hua, J., Swaddiwudhipong, S., Liu, Z.S., Xu, Q.Y.: Numerical analysis of nonlinear rotor–seal system. J. Sound Vib. 283, 525–542 (2005)

    Article  Google Scholar 

  10. Cheng, M., Meng, G., Jing, J.: Non-linear dynamics of a rotor–bearing–seal system. Arch. Appl. Mech. 76, 215–227 (2006)

    Article  MATH  Google Scholar 

  11. Shen, X., Zhao, M.: Effect of the seal force on nonlinear dynamics and stability of the rotor–bearing–seal system. J. Vib. Control 15, 197–217 (2009)

    Article  MathSciNet  Google Scholar 

  12. Ding, Q., Leung, A.Y.T.: Nonstationary processes of rotor/bearing system in bifurcation. J. Sound Vib. 268, 33–48 (2003)

    Article  Google Scholar 

  13. Ding, Q., Leung, A.Y.T.: Experimental study on nonlinear dynamic behaviors of a multi-bearing flexible rotor system. ASME J. Vib. Acoust. 127, 408–415 (2005)

    Article  Google Scholar 

  14. Younesian, D., Esmailzadeh, E.: Non-linear vibration of variable speed rotating viscoelastic beams. Nonlinear Dyn. 60, 193–205 (2010)

    Article  MATH  Google Scholar 

  15. Ansari, M., Esmailzadeh, E., Younesian, D.: Internal–external resonance of beams on non-linear viscoelastic foundation traversed by moving load. Nonlinear Dyn. 61, 163–182 (2010)

    Article  MATH  Google Scholar 

  16. Rega, G., Troger, H.: Dimension reduction of dynamical systems: methods, models, applications. Nonlinear Dyn. 4, 1–15 (2005)

    Article  MathSciNet  Google Scholar 

  17. Marion, M., Temam, R.: Nonlinear Galerkin methods. SIAM J. Numer. Anal. 26, 1139–1157 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  18. Matthies, H.G., Meyer, M.: Nonlinear Galerkin methods for the model reduction of nonlinear dynamical systems. Comput. Struct. 81, 1277–1286 (2003)

    Article  Google Scholar 

  19. Steindl, A., Troger, H.: Methods for dimension reduction and their application in nonlinear dynamics. Int. J. Solids Struct. 38, 2131–2147 (2001)

    Article  MATH  Google Scholar 

  20. Zhang, W.: A general mathematical model of nonlinear non-steady oil film force in dynamic load bearing. In: Wang, D.J., Qu, G.J. (eds.) Advances in Engineering Mechanics, pp. 158–167. Peking University Press, Beijing (1998)

    Google Scholar 

  21. Zhang, W., Xu, X.F.: Modeling of nonlinear oil-film force acting on a journal with unsteady and nonlinear instability analysis under the model. Int. J. Nonlinear Sci. Numer. Simul. 1, 179–186 (2000)

    Article  MATH  Google Scholar 

  22. Park, S., Chung, W.K., Youm, Y., Lee, J.W.: Natural frequencies and open-loop responses of an elastic beam fixed on a moving cart and carrying an intermediate lumped mass. J. Sound Vib. 230, 591–615 (2000)

    Article  Google Scholar 

  23. Low, K.H.: On the methods to derive frequency equations of beams carrying multiple masses. Int. J. Mech. Sci. 43, 871–881 (2001)

    Article  MATH  Google Scholar 

  24. Foias, C., Manley, O., Temam, R.: Modelling of the interaction of small and large eddies in two-dimensional turbulent flows. Math. Model. Numer. Anal. 22, 93–114 (1988)

    MathSciNet  MATH  Google Scholar 

  25. Ding, Q., Leung, A.Y.T., Cooper, J.E.: Dynamic analysis of a self-excited system with hysteretic non-linearity. J. Sound Vib. 245, 151–164 (2001)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Tianjin University, Tianjin, 300072, China

    Qian Ding & Kunpeng Zhang

  2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin, 300072, China

    Qian Ding & Kunpeng Zhang

Authors
  1. Qian Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kunpeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qian Ding.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ding, Q., Zhang, K. Order reduction and nonlinear behaviors of a continuous rotor system. Nonlinear Dyn 67, 251–262 (2012). https://doi.org/10.1007/s11071-011-9975-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-011-9975-8

Keywords

Search

Navigation