Abstract
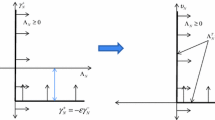
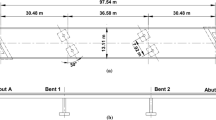
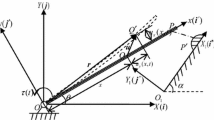
The oblique contact/impact of skew bridges triggers a unique rotational mechanism which earthquake reconnaissance reports correlate with deck unseating of such bridges. Building on the work of other researchers, the present study adopts a fully non-smooth rigid body approach and set-valued force laws, in order to analyze in depth this oblique multi-impact phenomenon. A linear complementarity formulation is proposed which yields a great variety of (multi-) impact states, depending on the initial (pre-impact) conditions, such as “slip” or “stick” at one corner (single-impact) or two corners (double-impact) of the body. The pertinent existential conditions of those impact states reveal a complex dynamic behavior. With respect to the rotational mechanism associated with double-impact, the physically feasible impact states as well as, counter-intuitive exceptions are recognized. The study proves that double oblique impact, both frictionless and frictional, may or may not produce rotation of the body and proposes criteria that distinguish each case. Most importantly, it is shown that the tendency of skew bridges to rotate (and hence unseat) after deck-abutment collisions is not a factor of the skew angle alone, but rather of the overall geometry in-plan, plus the impact parameters (coefficient of restitution and coefficient of friction). The study also provides a theoretical justification of the observed tendency of skew bridges to jam at the obtuse corner and rotate in such a way that the skew angle increases. Finally, counter-intuitive trends hidden in the response are unveiled which indicate that, due to friction, a skew bridge may also rotate so that the skew angle decreases.
Similar content being viewed by others
References
Dimitrakopoulos, E.G., Kappos, A.J., Makris, N.: Dimensional analysis of yielding and pounding structures for records without distinct pulses. Soil Dyn. Earthq. Eng. 29(7), 1170–1180 (2009)
Dimitrakopoulos, E.G., Makris, N., Kappos, A.J.: Dimensional analysis of the earthquake response of a pounding oscillator. ASCE J. Eng. Mech. (2009, in press)
Dimitrakopoulos, E.G., Makris, N., Kappos, A.J.: Dimensional analysis of the earthquake induced pounding between adjacent structures. Earthquake Eng. Struct. Dyn. 38(7), 867–886 (2009)
EERL (Earthquake Engineering Research Laboratory): Engineering features of the San Fernando earthquake of February 9, 1971. In: Jennings, P.C. (ed.) EERL 71-02 California Institute of Technology, Pasadena (1971)
Priestley, M.J.N., Seible, F., Calvi, G.M.: Seismic Design and Retrofit of Bridges. Wiley, New York (1996)
EERI: The Tehuacan, Mexico, Earhtquake of June 15, 1999. Special Earthquake Rep. September 1999 EERI, Oakland (1999)
Kim, S.H.: GIS-based regional risk analysis approach for bridges against earthquakes. Dissertation, Department of Civil Engineering, State University of New York at Buffalo (1993)
Maragakis, E., Jennings, P.C.: Analytical models for the rigid body motions of skew bridges. Earthquake Eng. Struct. Dyn. 15, 923–944 (1987)
Maleki, S.: Seismic modeling of skewed bridges with elastomeric bearings and side retainers. ASCE J. Bridge Eng. 10(4), 442–449 (2005)
Moreau, J.J.: Unilateral contact and dry friction in finite freedom dynamics. In: Moreau, J.J., Panagiotopoulos, P.D. (eds.) Non-Smooth Mechanics and Applications, CISM Courses and Lectures, vol. 302, pp. 1–82 Springer, New York (1988)
Panagiotopoulos, P.D.: Dynamic and incremental variational inequality principles, differential inclusions and their applications to co-existent phases problems. Acta Mech. 40, 85–107 (1981)
Panagiotopoulos, P.D.: Noncovex energy functions. Hemivariational inequalities and substationary principles. Acta Mech. 48, 111–130 (1983)
Glocker, C.: Set-Valued Force Laws. Springer, Berlin (2001)
Brogliato, B.: Nonsmooth Mechanics, 2nd edn. Springer, London (1999)
Leine, R.I., van Campen, D.H., Glocker, C.: Nonlinear dynamics and modeling of various wooden toys with impact and friction. J. Vib. Control 9, 25–78 (2003)
Payr, M., Glocker, C.: Oblique frictional impact of a bar: analysis and comparison of different impact laws. Nonlinear Dyn. 41, 361–383 (2005)
Brogliato, B., ten Dam, A.A., Paoli, L., Ge’not, F., Abadie, M.: Numerical simulation of finite dimensional multibody nonsmooth mechanical systems. Appl. Mech. Rev. 55(2), 107–150 (2002)
Pfeiffer, F.: Nonsmooth dynamics in engineering. In: Nonsmooth/Nonconvex Mechanics with Applications in Engineering, II. NNMAE—Proceedings of the International Conference. In MEMORIAM of Professor P.D. Panagiotopoulos, 7–8 July 2006, Thessaloniki, Greece, pp. 295–306 (2006)
Kwack, B.M., Lee, S.S.: A complementarity problem formulation for two-dimensional frictional contact problems. Comput. Struct. 28, 469–480 (1988)
Klarbring, A., Bjrrkman, G.: A mathematical programming approach to contact problem with friction and varying contact surface. Comput. Struct. 30, 1185–1198 (1988)
Pfeiffer, F., Glocker, C.: Multibody Dynamics with Unilateral Contacts. Wiley, New York (1996)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dimitrakopoulos, E.G. Analysis of a frictional oblique impact observed in skew bridges. Nonlinear Dyn 60, 575–595 (2010). https://doi.org/10.1007/s11071-009-9616-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-009-9616-7