Abstract
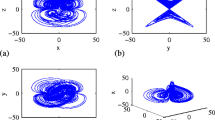
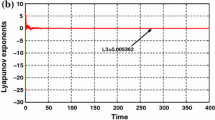
In this paper, several smooth canonical 3-D continuous autonomous systems are proposed in terms of the coefficients of nonlinear terms. These systems are derived from the existing 3-D four-wing smooth continuous autonomous chaotic systems. These new systems are the simplest chaotic attractor systems which can exhibit four wings. They have the basic structure of the existing 3-D four-wing systems, which means they can be extended to the existing 3-D four-wing chaotic systems by adding some linear and/or quadratic terms. Two of these systems are analyzed. Although the two systems are similar to each other in structure, they are different in dynamics. One is sensitive to the initializations and sampling time, but another is not, which is shown by comparing Lyapunov exponents, bifurcation diagrams, and Poincaré maps.
Similar content being viewed by others
References
Chua, L.O., Komuro, M., Matsumoto, T.: The double scroll family. IEEE Trans. Circuits Syst. I 33, 1072–1178 (1986)
Chua, L.O., Roska, T.: The CNN paradigm. IEEE. Trans. Circuits Syst. I C 40, 147–156 (1993)
Suykens, J.A.K., Chua, L.O.: n-double scroll hypercubes in 1-D CNNs. Int. J. Bifurc. Chaos 7, 1873–1885 (1997)
Suykens, J.A.K., Vandewalle, J.: Generation of n-double scrolls (n=1;2;3;4;…). IEEE Trans. Circuits Syst. I 40, 861–867 (1993)
Tang, K.S., Zhong, G.Q., Chen, G., Man, K.F.: Generation of n-scroll attractors via sine function. IEEE Trans. Circuits Syst. I 48, 1369–1372 (2001)
Yalcin, M.E., Ozoguz, S., Suykens, J.A.K., Vandewalle, J.: n-scroll chaos generators: a simple circuit model. Electron. Lett. 37, 147–148 (2001)
Yalcin, M.E., Suykens, J.A.K., Vandewalle, J., Ozoguz, S.: Families of scroll grid attractors. Int. J. Bifurc. Chaos 12, 23–41 (2002)
Lü, J., Yu, X., Chen, G.: Generating chaotic attractors with multiple merged basins of attraction: a switching piecewise-linear control approach. IEEE Trans. Circuits Syst. I 50, 198–207 (2003)
Lü, J., Han, F., Yu, X., Chen, G.: Generating 3-D multi-scroll chaotic attractors: a hysteresis series switching method. Automatica 40, 1677–1687 (2004)
Lü, J., Chen, G., Yu, X.: Design and analysis of multi-scroll chaotic attractors from saturated function series. IEEE Trans. Circuits Syst. I 51, 2476–2490 (1999)
Han, F., Yu, X., Lü, J., Chen, G., Feng, Y.: Generating multi-scroll chaotic attractors via a linear second-order hysteresis system. Dyn. Contin. Discrete Impulse Syst. Ser B, Appl. Algorithms 12, 95–110 (2005)
Qi, G.Y., Chen, G.R., van Wyk, M.A., van Wyk, B.J., et al.: A four-wing attractor generated from a new 3-D quadratic autonomous system. Chaos Solitons Fractals 38, 705–721 (2008)
Qi, G.Y., Chen, G., Li, S.W., Zhang, Y.H.: Four-wing attractors: from pseudo to real. Int. J. Bifurc. Chaos 16, 859–885 (2006)
Vanečěk, A., Čelikovský, S.: Control Systems from Linear Analysis to Synthesis of Chaos. Prentice-Hall, London (1996)
Chen, G., Ueta, T.: Yet another chaotic attractor. Int J. Bifurc. Chaos 9, 1465–1466 (1999)
Chen, G., Lü, J.: Dynamical Analysis, Control and Synchronization of the Generalized Lorenz Systems Family. Science Press, Beijing (2003) (in Chinese)
Čelikovský, S., Chen, G.: On the generalized Lorenz canonical form. Chaos Solitons Fractals 26, 1271–1276 (2005)
Qi, G.Y., Du, S.Z., Chen, G., Chen, Z.Q., Yuan, Z.Z.: On a four-dimensional chaotic system. Chaos Solitons Fractals 23, 1671–1676 (2005)
Qi, G.Y., Chen, G.R., Zhang, Y.H.: Analysis and circuit implementation of a new 4-D chaotic system. Phys. Lett. A 352, 386–397 (2006)
Qi, G.Y., Barend, J., Michael, A.: A four-wing attractor and its analysis. Chaos Solitons Fractals 40, 2016–2030 (2009)
Elwakil, A.S., Özoǧz, S., Kennedy, M.P.: A four-wing butterfly attractor from a fully autonomous system. Int. J. Bifurc. Chaos 13, 3093–3098 (2003)
Liu, W.B., Chen, G.: A new chaotic system and its generation. Int. J. Bifurc. Chaos 13, 261–266 (2003)
Liu, W.B., Chen, G.: Dynamical analysis of a chaotic system with two double-scroll chaotic attractors. Int. J. Bifurc. Chaos 14, 971–998 (2004)
Liu, W.B., Chen, G.: Can a three-dimensional smooth autonomous quadratic chaotic system generate a single four-scroll attractor? Int. J. Bifurc. Chaos 14, 1395–1403 (2004)
Lü, J.: A new chaotic system and beyond: the generalized Lorenz-like system. Int. J. Bifurc. Chaos 14, 1507–1537 (2004)
Zhou, T.S., Chen, G.: Classification of chaos in 3-D automations quadratic system, I: basic framework and methods. Int. J. Bifurc. Chaos 16, 2459–2479 (2006)
Chen, Z., Yang, Y., Yuan, Z.: A single three-wing or four-wing chaotic attractor generated from a three-dimensional smooth quadratic autonomous system. Chaos Solitons Fractals 38, 1187–1196 (2008)
Wang, L.: 3-scroll and 4-scroll chaotic attractors generated from a new 3-D quadratic autonomous system. Nonlinear Dyn. (2008). doi:10.1007/s11071-008-9417-4
Lorenz, E.N.: Deterministic non-periodic flow. J. Atmos. Sci. 20, 130–141 (1963)
Čelikovský, S., Vaněček, A.: Bilinear systems and chaos. Kybernetika 30, 403–424 (1994)
Čelikovský, S., Chen, G.: On a generalized Lorenz canonical form of chaotic systems. Int. J. Bifurc. Chaos 12, 1789–1812 (2002)
Lü, J., Chen, G., Cheng, D., Čelikovský, S.: Bridge the gap between the Lorenz system and the Chen system. Int J. Bifurc. Chaos 12, 2917–2928 (2002)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, Z., Qi, G., Sun, Y. et al. A new type of four-wing chaotic attractors in 3-D quadratic autonomous systems. Nonlinear Dyn 60, 443–457 (2010). https://doi.org/10.1007/s11071-009-9607-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-009-9607-8