Abstract
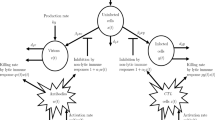
In this paper, the propagation of a nonlinear delay SIR epidemic using the double epidemic hypothesis is modeled. In the model, a system of impulsive functional differential equations is studied and the sufficient conditions for the global attractivity of the semi-trivial periodic solution are drawn. By use of new computational techniques for impulsive differential equations with delay, we prove that the system is permanent under appropriate conditions. The results show that time delay, pulse vaccination, and nonlinear incidence have significant effects on the dynamics behaviors of the model. The conditions for the control of the infection caused by viruses A and B are given.
Article PDF
Similar content being viewed by others
References
Enjuanes, L., Sanchez, C., Gebauer, F., Mendez, A., Dopazo, J., Ballesteros, M.L.: Evolution and tropism of transmissible gastroenteritis coronavirus. Adv. Exp. Med. Biol. 342, 35–42 (1993)
Beretta, E., Takeuchi, Y.: Global stability of an SIR epidemic model with time delays. J. Math. Biol. 33(3), 250–260 (1995)
Beretta, E., Hara, T., Ma, W.B., Takenchi, Y.: Global asymptotic stability of an SIR epidemic model with distributed time delay. Nonlinear Anal. 47, 4107–4115 (2001)
Takeuchi, Y., Ma, W.B., Beretta, E.: Global asymptotic properties of a delay SIR epidemic model with finite incubation times. Nonlinear Anal. 42, 931–947 (2000)
Ma, W.B., Song, M., Takeuchi, Y.: Global stability of an SIR epidemic model with time delay. Appl. Math. Lett. 17, 1141–1145 (2004)
Song, M., Ma, W.B., Takeuchi, Y.: Permanence of a delayed SIR epidemic model with density dependent birth rate. J. Comput. Appl. Math. 201(2), 389–394 (2007)
Ma, W.B., Takeuchi, Y., Hara, T., Beretta, E.: Permanence of an SIR epidemic model with distributed time delays. Tohoku Math. J. 54, 581–591 (2002)
Zhang, T.L., Teng, Z.D.: Permanence and extinction for a nonautonomous SIRS epidemic model with time delay. Appl. Math. Model. 33(2), 1058–1071 (2009)
Zhang, T.L., Teng, Z.D.: Global behavior and permanence of SIRS epidemic model with time delay. Nonlinear Anal.: Real World Appl. 9(4), 1409–1424 (2008)
Meng, X.Z., Chen, L.S.: The dynamics of a new SIR epidemic model concerning pulse vaccination strategy. Appl. Math. Comput. 197(2), 582–597 (2008)
Shulgin, B., Stone, L., Agur, Z.: Pulse vaccination strategy in the SIR epidemic model. Bull. Math. Biol. 60, 1–26 (1998)
Lu, Z.H., Chi, X.B., Chen, L.S.: The effect of constant and pulse vaccination on SIR epidemic model with horizontal and vertical transmission. Math. Comput. Model. 36, 1039–1057 (2002)
D’Onofrio, A.: On pulse vaccination strategy in the SIR epidemic model with vertical transmission. Appl. Math. Lett. 18, 729–732 (2005)
Hui, J., Chen, L.S.: Impulsive vaccination of SIR epidemic models with nonlinear incidence rates. Discrete Continuous Dyn. Syst. Ser. B 4, 595–605 (2004)
DeQuadros, C.A., Andrus, J.K., Olive, J.M.: Eradication of the poliomyelitis, progress. Am. Pediatr. Infect. Dis. J. 10(3), 222–229 (1991)
Ramsay, M., Gay, N., Miller, E.: The epidemiology of measles in England and Wales: Rationale for 1994 nation vaccination campaign. Commun. Dis. Rep. 4(12), 141–146 (1994)
Sabin, A.B.: Measles, killer of millions in developing countries: Strategies of elimination and continuation control. Eur. J. Epidemiology 7, 1–22 (1991)
Zhang, H., Georgescu, P., Chen, L.S.: An impulsive predator–prey system with Beddington–Deangelis functional response and time delay. Int. J. Biomath. 1(1), 1–17 (2008)
Sun, S.L., Chen, L.S.: Permanence and complexity of the eco-epidemiological model with impulsive perturbation. Int. J. Biomath. 1(2), 121–132 (2008)
Liu, B., Teng, Z.D., Liu, W.B.: Dynamic behaviors of the periodic Lotka–Volterra competing system with impulsive perturbations. Chaos Solitons Fractals 31(2), 356–370 (2007)
Li, Z.X., Chen, L.S.: Periodic solution of a turbidostat model with impulsive state feedback control. Nonlinear Dyn. (in press). doi10.1007/s11071-009-9498-8
Wei, C.J., Chen, L.S.: Dynamic analysis of mathematical model of ethanol fermentation with gas stripping. Nonlinear Dyn. 57(1–2), 13–23 (2009)
Shi, R.Q., Chen, L.S.: The study of a ratio-dependent predator–prey model with stage structure in the prey. Nonlinear Dyn. (in press). doi10.1007/s11071-009-9491-2
Cooke, K.L.: Stability analysis for a vector disease model. Rocky Mt. J. Math. 9, 31–42 (1979)
Wei, H., Li, X., Martcheva, M.: An epidemic model of a vector-borne disease with direct transmission and time delay. J. Math. Anal. Appl. 342, 895–908 (2008)
Mukandavire, Z., Garira, W., Chiyaka, C.: Asymptotic properties of an HIV/AIDS model with a time delay. J. Math. Anal. Appl. 330, 916–933 (2007)
McCluskey, C.: Global stability for a class of mass action systems allowing for latency in tuberculosis. J. Math. Anal. Appl. 338, 518–535 (2008)
Beretta, E., Luang, Y.: Modeling and analysis of a marine bacteriophage infection with latency period. Nonlinear Anal.: Real World Appl. 2, 35–74 (2001)
Ghosh, S., Bhattacharyya, S., Bhattacharya, D.K.: Role of latency period in viral infection: A pest control model. Math. Biosci. 210, 619–646 (2007)
Meng, X., Chen, L., Cheng, H.: Two profitless delays for the SEIRS epidemic disease model with nonlinear incidence and pulse vaccination. Appl. Math. Comput. 186, 516–529 (2007)
Wei-min, Levin, S.A., Lwasa, Y.: Influence of nonlinear incidence rates upon the behavior of SIRS Epidemiological models. J. Math. Biol. 25, 359–380 (1987)
Wei-min, Hethcote, H.W., Levin, S.A.: Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 23, 187–240 (1986)
Lakshmikantham, V., Bainov, D., Simeonov, P.: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Kuang, Y.: Delay Differential Equations with Applications in Population Dynamics. Academic Press, San Diego (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
This project was supported by the National Natural Science Foundation of China (No. 30870397) and National Basic Research Program of China (973 Program) (No. 2006CB403207-4).
Rights and permissions
About this article
Cite this article
Meng, X., Li, Z. & Wang, X. Dynamics of a novel nonlinear SIR model with double epidemic hypothesis and impulsive effects. Nonlinear Dyn 59, 503–513 (2010). https://doi.org/10.1007/s11071-009-9557-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-009-9557-1