Abstract
It has become commonly accepted by scientists and engineers that brake squeal is generated by friction-induced self-excited vibrations of the brake system. The noise-free configuration of the brake system loses stability through a flutter-type instability and the system starts oscillating in a limit cycle. Usually, the stability analysis of disk brake models, both analytical as well as finite element based, investigates the linearized models, i.e. the eigenvalues of the linearized equations of motion. However, there are experimentally observed effects not covered by these analyses, even though the full nonlinear models include these effects in principle.
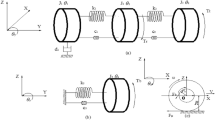
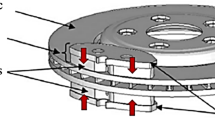
The present paper describes the nonlinear stability analysis of a realistic disk brake model with 12 degrees of freedom. Using center manifold theory and artificially increasing the degree of degeneracy of the occurring bifurcation, an analytical expression for the turning points in the bifurcation diagram of the subcritical Hopf bifurcations is calculated. The parameter combination corresponding to the turning points is considered as the practical stability boundary of the system. Basic phenomena known from the operating experience of brake systems tending to squeal problems can be explained on the basis of the practical stability boundary.
Access this article
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Similar content being viewed by others
References
Ibrahim, R.: Friction-induced vibration, chatter, squeal and chaos, part I: Mechanics of contact and friction. Appl. Mech. Rev. 47(7), 209–226 (1994)
Ibrahim, R.: Friction-induced vibration, chatter, squeal and chaos, part II: Dynamic and modeling. Appl. Mech. Rev. 47(7), 227–253 (1994)
Chen, F., Tan, C.A., Quaglia, R.L.: Disc Brake Squeal: Mechanism, Analysis, Evaluation and Reduction/Prevention. SAE International, Warrendale (2006)
Ouyang, H., Mottershead, J., Cartmell, M., Friswell, M.: Friction-induced parametric resonances in discs: effect of a negative friction–velocity relationship. J. Sound Vib. 209(2), 251–264 (1998)
Shin, K., Brennan, M., Oh, J.E., Harris, C.: Analysis of disk brake noise using a two-degree-of-freedom model. J. Sound Vib. 254(5), 837–848 (2002)
Millner, N.: An analysis of disc brake squeal. SAE Technical Paper Series, 780332 (1978)
Popp, K., Rudolph, M., Kröger, M., Lindner, M.: Mechanisms to generate and avoid friction-induced vibrations. VDI-Bericht 1736, 1–15 (2002)
von Wagner, U., Hochlenert, D., Hagedorn, P.: Minimal models for disk brake squeal. J. Sound Vib. 302, 527–539 (2007)
Hochlenert, D., Spelsberg-Korspeter, G., Hagedorn, P.: Friction-induced vibrations in moving continua and their application to brake squeal. ASME J. Appl. Mech. 74, 542–549 (2007)
Jearsiripongkul, T.: Squeal in floating caliper disk brakes: A mathematical model. Ph.D. thesis, Technische Universität Darmstadt (2005)
Spelsberg-Korspeter, G., Hochlenert, D., Kirillov, O.N., Hagedorn, P.: In- and out-of-plane vibrations of a rotating plate with frictional contact: investigations on squeal phenomena. ASME J. Appl. Mech. (2007, accepted for publication)
Giannini, O., Akay, A., Massi, F.: Experimental analysis of brake squeal noise on a laboratory brake setup. J. Sound Vib. 292, 1–20 (2006)
Sinou, J., Thouverez, F., Jezequel, L.: Analysis of friction and instability by the centre manifold theory for a non-linear sprag–slip model. J. Sound Vib. 265(3), 527–559 (2003)
Hochlenert, D.: Selbsterregte Schwingungen in Scheibenbremsen: Mathematische Modellbildung und aktive Unterdrückung von Bremsenquietschen. Ph.D. thesis, Technische Universität Darmstadt (2006)
Troger, H., Steindl, H.: Nonlinear Stability and Bifurcation Theory. Springer, Wien (1991)
Xu, G., Troger, H., Steindl, A.: Global analysis of the loss of stability of a special railway bogie. In: Schiehlen, W. (ed.) Nonlinear Dynamics in Engineering Systems. Springer, Berlin (1990)
Rand, R., Armbruster, D.: Perturbation Methods, Bifurcation Theory and Computer Algebra. Springer, New York (1988)
Golubitsky, M., Schaeffer, D.: Singularities and Groups in Bifurcation Theory. Springer, New York (1985)
Seyranian, A.P., Mailybaev, A.A.: Multiparameter Stability Theory with Mechanical Applications. World Scientific, Singapore (2003)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hochlenert, D. Nonlinear stability analysis of a disk brake model. Nonlinear Dyn 58, 63–73 (2009). https://doi.org/10.1007/s11071-008-9461-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-008-9461-0