Skip to main content
SpringerLink
Log in

Dynamic controller design for a class of nonlinear uncertain systems subjected to time-varying disturbance

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

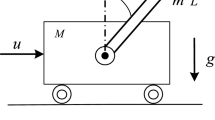
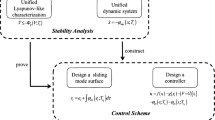
Abstract

Inheriting advantages of both proportional-integral-derivative controller and standard sliding mode control theory, a synthetic controller design for a class of nonlinear system is presented. Regarding the architecture of the developed controller, it does not include model-based nominal control term so that the method eliminates complicated processes for system parameters identification and design of extra compensators. With simple gain tuning rules, the proposed control algorithm provides global asymptotical stability and is capable of alleviating discontinuous control switching considerably. A self-sustained oscillations phenomenon caused by the proposed control configuration is also further addressed. Simulations and experiments are conducted to verify the feasibility and applicability of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Soylemez, M.T., Munro, N., Baki, H.: Fast calculation of stabilizing PID controllers. Automatica 39(1), 121–126 (2003)

    Article  MathSciNet  Google Scholar 

  2. Alvarez-Ramirez, J., Cervantes, I., Kelly, R.: PID regulation of robot manipulators: stability and performance. Syst. Control Lett. 41(2), 73–83 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  3. Chen, W.H., Ballance, D.J., Gawthrop, P.J., O’Reilly, J.: A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 47(4), 932–938 (2000)

    Article  Google Scholar 

  4. Liu, Z.L., Svoboda, J.: A new control scheme for nonlinear systems with disturbances. IEEE Trans. Control Syst. Technol. 14(1), 176–181 (2006)

    Article  Google Scholar 

  5. Ding, Z.: Asymptotic rejection of asymmetric periodic disturbances in output-feedback nonlinear systems. Automatica 43(3), 555–561 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  6. Ding, Z.: Asymptotic rejection of unmatched general periodic disturbances in a class of nonlinear systems. IEE Proc. Control Theory Appl. 2(4), 269–276 (2008)

    Article  Google Scholar 

  7. Ding, Z.: Asymptotic rejection of finite frequency modes of general periodic disturbances in output feedback nonlinear systems. Automatica 44(9), 2317–2325 (2008)

    Article  MATH  Google Scholar 

  8. Jafarov, E.M., Parlakci, M.N.A., Istefanopulos, Y.: A new variable structure PID-controller design for robot manipulators. IEEE Trans. Control Syst. Technol. 13(1), 122–130 (2005)

    Article  Google Scholar 

  9. Huang, Y.J., Wang, J.Y.: Steady-state analysis for a class of sliding mode controlled systems using describing function method. Nonlinear Dyn. 30(3), 223–241 (2002)

    Article  MATH  Google Scholar 

  10. Slotine, J.J.E., Li, W.: Applied Nonlinear Control. Prentice-Hall, New Jersey (1991)

    MATH  Google Scholar 

  11. Chen, M.S., Hwang, Y.R., Tomizuka, M.: A state-dependent boundary layer design for sliding mode control. IEEE Trans. Autom. Control 47(10), 1677–1681 (2002)

    Article  MathSciNet  Google Scholar 

  12. Sira-Ramirez, H.: On the dynamical sliding mode control of nonlinear systems. Int. J. Control 57(5), 1039–1061 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  13. Bartolini, G., Ferrara, A., Usai, E.: Chattering avoidance by second-order sliding mode control. IEEE Trans. Autom. Control 43(2), 241–246 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  14. Kachroo, P.: Existence of solution to a class of nonlinear convergent chattering free SMC systems. IEEE Trans. Autom. Control 44(8), 1620–1624 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  15. Chen, C.L., Xu, R.L.: Tracking control of robot manipulator using sliding mode controller with performance robustness. ASME J. Dyn. Syst. Meas. Control 121(1), 64–70 (1999)

    Article  Google Scholar 

  16. Peng, C.C., Chen, C.L.: Biaxial contouring control with friction dynamics using a contour index approach. Int. J. Mach. Tools Manuf. 47(10), 1542–1555 (2007)

    Article  Google Scholar 

  17. Suzuki, S., Pan, Y.D., Furuta, K.: Walking control by chattering-free VS servo using passive walking trajectory. Int. J. Control 76(9–10), 1034–1046 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  18. Chen, M.S., Chen, C.H., Yang, F.Y.: An LTR-observer-based dynamic sliding mode control for chattering reduction. Automatica 43(6), 1111–1116 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  19. Parra-Vega, V., Hirzinger, G.: Chattering-free sliding mode control for a class of nonlinear mechanical systems. Int. J. Robust Nonlinear Control 11(12), 1161–1178 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  20. Parra-Vega, V., Arimoto, S., Liu, Y.H., Hirzinger, G., Akella, P.: Dynamic sliding PID control for tracking of robot manipulators: theory and experiments. IEEE Trans. Robot. Autom. 19(6), 967–976 (2003)

    Article  Google Scholar 

  21. Arteaga, M.A., Castillo-Sanchez, A., Parra-Vega, V.: Cartesian control of robots without dynamic model and observer design. Automatica 42(3), 473–480 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Zanasi, R.: Sliding mode using discontinuous control algorithm of integral type. Int. J. Control 57(5), 1079–1099 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  23. Emelyanov, S.V., Korovin, S.K.: Control of Complex and Uncertain Systems: New Types of Feedback. Springer, London (2000)

    Google Scholar 

  24. Xian, B., Dawson, D.M., de Queiroz, M.S., Chen, J.: A continuous asymptotic tracking control strategy for uncertain nonlinear systems. IEEE Trans. Autom. Control 49(7), 1206–1211 (2004)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aeronautics and Astronautics, National Cheng Kung University Tainan, Tainan, Taiwan

    Chao-Chung Peng & Chieh-Li Chen

Authors
  1. Chao-Chung Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chieh-Li Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chieh-Li Chen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Peng, CC., Chen, CL. Dynamic controller design for a class of nonlinear uncertain systems subjected to time-varying disturbance. Nonlinear Dyn 57, 411–423 (2009). https://doi.org/10.1007/s11071-008-9451-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-008-9451-2

Keywords

Search

Navigation