Abstract
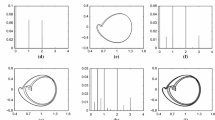
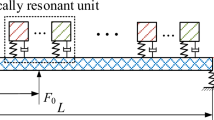
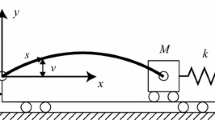
In this paper, the nonlinear characteristics of the parametric resonance of simply supported elastic beams are investigated. Considering a geometrically exact formulation for unsharable and inextensible elastic beams subject to support motions, the integral-partial-differential equation of motion is obtained. The third-order perturbation of the equation of motion is then determined in a form amenable to an asymptotic treatment. The method of multiple scales is used to obtain the equations that describe the modulation of the amplitude and phase of parametric-resonance motions. The stability and bifurcations of the system are investigated considering, in particular, the frequency-response function. Furthermore, experimental results are shown to confirm the theoretically predicted stability and bifurcations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Antman, S.S.: Nonlinear Problems of Elasticity, 2nd edn. New York, Springer (2005)
Villaggio, P.: Mathematical Models for Elastic Structures. Cambridge University Press, Cambridge (1997)
Cosserat, E., Cosserat, F.: Theorie des corps deformables. Herman, Paris (1909)
Starzewski, M.O., Jasiuk, I.: Stress invariance in planar Cosserat elasticity. Proc. R. Soc. Lond. A 451, 453–470 (1995)
Eisley, J.G.: Nonlinear vibration of beams and rectangular plates. Z. Angew. Math. Mech. 15 (1964)
Lacarbonara, W., Paolone, A., Yabuno, H.: Modeling of planar nonshallow prestressed beams towards asymptotic solutions. Mech. Res. Commun. 31, 301–310 (2004)
Lacarbonara, W., Yabuno, H.: Refined models of elastic beams undergoing large in-plane motions: Theory and experiment. Int. J. Solids Struct. 43, 5066–5084 (2006)
Dugundji, J., Mukhopadhyay, V.: Lateral bending-torsion vibrations of a thin beam under parametric excitation. ASME J. Appl. Mech. Trans. 9, 693–698 (1973)
Saito, H., Sato, K., Otomi, K.: Nonlinear forced vibrations of a beam carrying concentrated mass under gravity. J. Sound Vib. 46(4), 515–525 (1976)
Yabuno, H., Nayfeh, A.H.: Nonlinear normal modes of a parametrically excited cantilever beam. Nonlinear Dyn. 25, 65–77 (2001)
Evensen, J.A., Evan-Iwanowski, R.M.: Effects of longitudinal inertia upon the parametric response of elastic columns. J. Appl. Mech. 33, 141–148 (1996)
Nayfeh, A.H., Pai, P.F.: Non-linear non-planar parametric responses of an inextensional beam. Int. J. Non-Linear Mech. 24(2), 139–158 (1989)
Yabuno, H., Ide, Y., Aoshima, N.: Nonlinear analysis of a parametrically excited cantilever beam (effect of the tip mass on stationary response). JSME Int. J. 41(3), 555–562 (1998)
Anderson, T.J., Nayfeh, A.H., Balachandran, B.: Experimental verification of the importance of the nonlinear curvature in the response of a cantilever beam. J. Vib. Acoust. 118, 21–27 (1996)
Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1979)
Yabuno, H., Koda, T.: Identification of Coulomb friction at supporting points of a hinged-hinged beam. J. Syst. Des. Dyn. 1, 352–361 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Son, IS., Uchiyama, Y., Lacarbonara, W. et al. Simply supported elastic beams under parametric excitation. Nonlinear Dyn 53, 129–138 (2008). https://doi.org/10.1007/s11071-007-9301-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-007-9301-7