Skip to main content
SpringerLink
Log in

Time-optimal swing-up feedback control of a pendulum

  • Original Article
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

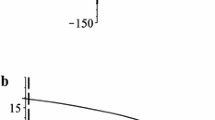
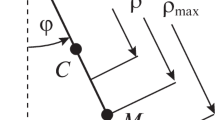
Time-optimal feedback control is obtained that brings a pendulum to the upper unstable equilibrium position. The solution is based on the maximum principle and involves analytical investigations combined with numerical computations. As a result, the switching and dispersal curves that bound the domains in the phase plane corresponding to different values of the optimal bang-bang control are constructed for various values of the maximal admissible control torque.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. K.J., Furuta, K.: Swinging up a pendulum by energy control. In: Proceeding of the Congress on the International Federation of Automatic Control, Vol.E. pp. 87–95 (1996)

    Google Scholar 

  2. Åström, K.J., Furuta, K.: Swinging up a pendulum by energy control. Automatica 36(2), 287–295 (2000)

    Article  MathSciNet  Google Scholar 

  3. Faronov, V.V.: Programming on Personal Computers in Turbo-pascal Environment. Moscow: MGTU press (in Russian). (1991

  4. Fehlberg, E.: Low-Order Classical Runge-Kutta Formulas with Stepsize Control. NASA Technical Report R-315 (1969)

  5. Fehlberg, E.: Klassische Runge-Kutta-formeln vierter und niedregerer Ordnung mit Schrittweitenkontrolle und ihre Anwendung auf Warmeleitungs-probleme. Computing 6, 61–71 (1970)

    Article  MathSciNet  Google Scholar 

  6. Forsythe, G.E., Malcolm, M.A., Moler, C.B.: Computer methods for Mathematical Computations. Prentice-Hall Englewood Cliffs, N J (1977)

  7. Furuta, K.: Super mechano-systems: fusion of control and mechanism. In: Proceeding of the Congress on the International Federation of Automatic Control 15th Triennial World Congress, Barcelona, Spain. (2002)

  8. Grishin, A.A., Lenskii, A.V., Okhotsimsky, D.E., Panin, D.A., Formal'skii, A.M.: A control synthesis for a unstable object: an inverted pendulum'. J. Comput. Syst. Sci. Int. (5), 14–24 (2002)

    Google Scholar 

  9. Kapitsa, P.L.: Dynamic stability of a pendulum with oscillating suspension point. ZhETF 21(5) (1951) (in Russian)

  10. Lee, E.B., Markus, L.: Foundations of Optimal Control Theory. Wiley New York, London, Sydney (1967)

  11. Pontryagin, L.S., Boltyanskii, V.G., Gamkrelidze, R.V., Mishchenko, E.F.: The Mathematical Theory of Optimal Processes. Wiley New York (1962)

  12. Shampine, L.E., Watts, H.A., Davenport, S.: Solving non-stiff ordinary differential equations – the state of the art'. Sandia Laboratories Report SAND75-0182, Albuquerque, NM; SIAM Review 18(3), 376–411 (1976)

    Google Scholar 

  13. Stephenson, A.: On a new type of dynamical stability'. Memoirs and Proceedings of the Manchester Literary and Philosophical Society 52(8), Pt.2 (1908)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute for Problems in Mechanics of the Russian Academy of Sciences, 101-1 prosp. Vernadskogo, Moscow, 119526, Russia

    F. L. Chernousko & S. A. Reshmin

Authors
  1. F. L. Chernousko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. A. Reshmin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. L. Chernousko.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chernousko, F.L., Reshmin, S.A. Time-optimal swing-up feedback control of a pendulum. Nonlinear Dyn 47, 65–73 (2007). https://doi.org/10.1007/s11071-006-9059-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-006-9059-3

Keywords

Search

Navigation