Abstract
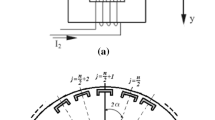
In this paper, we use the asymptotic perturbation method to investigate nonlinear oscillations and chaotic dynamics in a rotor-active magnetic bearings (AMB) system with 8-pole legs and the time-varying stiffness. The stiffness in the AMB is considered as the time varying in a periodic form. Because of considering the weight of the rotor, the formulation on the electromagnetic force resultants includes the quadratic and cubic nonlinearities. The resulting dimensionless equations of motion for the rotor-AMB system with the time-varying stiffness in the horizontal and vertical directions are a two-degree-of-freedom nonlinear system with quadratic and cubic nonlinearities and parametric excitation. The asymptotic perturbation method is used to obtain the averaged equations in the case of primary parametric resonance and 1/2 subharmonic resonance. It is found that there exist period-3, period-4, period-6, period-7, period-8, quasiperiodic and chaotic modulated amplitude oscillations in the rotor-AMB system with the time-varying stiffness. It is seen from the numerical results that there are the phenomena of the multiple solutions and the soft-spring type and the hardening-spring type in nonlinear frequency-response curves for the rotor-AMB system. The parametric excitation, or the time-varying stiffness produced by the PD controller is considered to be a controlling force which can control the chaotic response in the rotor-AMB system to a period n motion.
Similar content being viewed by others
References
Nayfeh, A. H. and Mook, D. T., Nonlinear Oscillations, Wiley-Interscience, New York, 1979.
Bajaj, A. K., ‘Bifurcations in a parametrically excited nonlinear oscillator’, International Journal of Non-Linear Mechanics 22, 1987, 47–59.
Zhang, W. and Huo, Q. Z., ‘Bifurcations of nonlinear oscillation system under combined parametric and forcing excitation’, Acta Mechanica Sinica 23, 1991, 464–474.
Zhang, W. and Ye, M., ‘Local and global bifurcations of valve mechanism’, Nonlinear Dynamics 6, 1994, 301–316.
Zhang, W., ‘Further studies for nonlinear dynamics of one dimensional crystalline beam’, Acta Physica Sinica (Overseas Edition) 5, 1996, 409–422.
Wang, K. W. and Lai, J. S., ‘Parametric control of structural vibrations via adaptable stiffness dynamic absorbers’, ASME Journal of Vibration and Acoustics 118, 1996, 41–47.
Zhang, W. and Zu, J. W., ‘Nonlinear dynamic analysis for a rotor-active magnetic bearing system with time-varying stiffness, Part I. Formulation and local bifurcation’, in Proceedings of 2003 ASME International Mechanical Engineering Congress & Exposition, Washington DC, November 16–21, 2003, ASME, New York, 2003, pp. 631–640.
Mohamed, A. M. and Emad, F. P., ‘Nonlinear oscillations in magnetic bearing system’, IEEE Transactions on Automatic Control 38, 1993, 1242–1245.
Virgin, L. N., Walsh, T. F., and Knight, J. D., ‘Nonlinear behavior of a magnetic bearing system’, ASME Journal of Engineering for Gas Turbines and Power 117, 1995, 582–588.
Chinta, M. and Palazzolo, A. B., ‘Stability and bifurcation of rotor motion in a magnetic bearing’, Journal of Sound and Vibration 214, 1998, 793–803.
Wang, X. and Noah, S., ‘Nonlinear dynamics of a magnetically supported rotor on safety auxiliary bearings’, ASME Journal of Vibration and Acoustics 120, 1998, 596–606.
Ji, J. C., Yu, L., and Leung, A. Y. T., ‘Bifurcation behavior of a rotor by active magnetic bearings’, Journal of Sound and Vibration 235, 2000, 133–151.
Ji, J. C. and Hansen, C. H., ‘Nonlinear oscillations of a rotor in active magnetic bearings’, Journal of Sound and Vibration 240, 2001, 599–612.
Maccari, A., ‘Approximate solution of a class of nonlinear oscillators in resonance with a periodic excitation’, Nonlinear Dynamics 15, 1998, 329–343.
Maccari, A., ‘Dissipative bidimensional systems and resonant excitation’, International Journal of Non-Linear Mechanics 33, 1998, 713–726.
Maccari, A., ‘Modulated motion and infinite-period homoclinic bifurcation for parametrically excited Lienard systems’, International Journal of Non-Linear Mechanics 35, 2000, 239–262.
Maccari, A., ‘The Kadomtsev-Petviashvili equation as source of integrable model equations’, Journal of Mathematical Physics 37, 1996, 6207–6212.
Maccari, A., ‘A model system for the behavior of two non-linearly coupled oscillators’, Journal of Sound and Vibration 215, 1998, 313–330.
Ye, M., Sun, Y. H., Zhang, W., Zhan, X. P., and Ding, Q., ‘Nonlinear oscillations and chaotic dynamics of an antisymmetric cross-ply laminated composite rectangular thin plate under parametric excitation’, International Journal of Bifurcations and Chaos, in press.
Wen, B. C., Gu, J. L., Xia, S. B., and Wang, Z., Advanced Dynamics of Rotor, China Machine Industry Press, Beijing, 2000.
Siegwart, R., Design and Application of Active Magnetic Bearing (AMB) for Vibration Control, von Karman Institute Fluid Dynamics Lecture Series 1992-06, Vibration and Rotor Dynamics, 1992.
Nusse, H. E. and Yorke, J. A., Dynamics: Numerical Explorations, Springer-Verlag, New York, Berlin, 1997.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, W., Zhan, X.P. Periodic and Chaotic Motions of a Rotor-Active Magnetic Bearing with Quadratic and Cubic Terms and Time-Varying Stiffness. Nonlinear Dyn 41, 331–359 (2005). https://doi.org/10.1007/s11071-005-7959-2
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11071-005-7959-2