Abstract
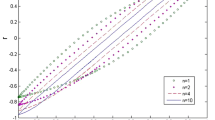
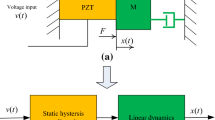
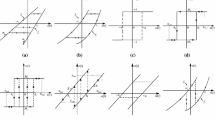
This paper deals with the problem of identifying the parameters of the hysteretic Bouc–Wen model. In the existing literature, the methods devoted to this problem rely mainly on numerical simulations and do not have, to a very large extent, a rigorous mathematical justification. Our method consists in exciting the hysteretic system with a periodic input and obtain the desired parameters from the resulting limit cycle. The identification method that we propose has a rigorous mathematical basis as it based on the analytic description of the limit cycle, and, unlike existing identification methods for the Bouc–Wen model, gives guaranteed relative errors between the (unknown) exact model parameters and their corresponding estimates. We also prove that this method is robust with respect to constant and T-periodic disturbances commonly present in any laboratory experiment. A numerical simulation example illustrates the use of our identification method.
Similar content being viewed by others
References
Brailovski, V., Prokoshkin, S., Terriault, P., and Trochu, F., ‘Shape Memory Alloys: Fundamentals, Modeling and Applications’, Université du Québec, École de Technologie Supérieure, National Library of Canada, 2003.
Faravelli, L., ‘Modelling the response of an elastomeric base isolator’, Journal of Structural Control 8(1), 2001, 17–30.
Ni, Y. Q., Ko, J. M., and Wong, C. W., ‘Identification of non-linear hysteretic isolators from periodic vibration tests’, Journal of Sound and Vibration 217(4), 1998, 737–756.
Smyth, A. W., Masri, S. F., Kosmatopoulos, E. B., Chassiakos, A. G., and Caughey, T. K., ‘Development of adaptive modeling techniques for non-linear hysteretic systems’, International Journal of Non-Linear Mechanics 37, 2002, 1435–1451.
Author information
Authors and Affiliations
Corresponding author
Additional information
Contributed by Prof. F. Casciati.
Rights and permissions
About this article
Cite this article
Ikhouane, F., Rodellar, J. On the Hysteretic Bouc–Wen Model. Nonlinear Dyn 42, 79–95 (2005). https://doi.org/10.1007/s11071-005-0070-x
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11071-005-0070-x