Skip to main content
SpringerLink
Log in

A simplified mathematical model for the dam-breach hydrograph for three reservoir geometries following a sudden full dam break

  • Original Paper
  • Published:
Natural Hazards Aims and scope Submit manuscript

Abstract

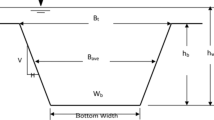
The prediction of dam-break water flow at dam site is essential to reduce the potential for loss of damage in the downstream floodplain. In this study, the influence of reservoir shapes (rectangular, trapezoidal and triangular wedge) on dam-break discharge hydrographs at a dam site was investigated to estimate the peak discharge and discharge hydrograph quickly. By assuming instantaneous and complete breaches to simplify the discharge process, a formula for the peak discharge and a simple analytical solution to the entire discharge hydrograph following a dam break at the dam site were generated. The discharge hydrograph at the dam site derived by the proposed mathematical model was validated through a comparison with the results calculated by the numerical simulation and other existing approaches. The outflow discharges calculated by both the mathematical and numerical model was very similar under the conditions of the three different reservoir shapes. The overall discharge hydrograph shape was mainly influenced by the length of the reservoir, while the magnitude of the outflow discharge was primarily affected by the initial water depth.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Aureli F, Maranzoni A, Mignosa P (2014) A semi-analytical method for predicting the outflow hydrograph due to dam-break in natural valleys. Adv Water Resour 63(2):38–44

    Article  Google Scholar 

  • Bellos CV, Soulis JV, Sakkas JG (1991) Computation of two-dimensional dam-break induced flows. Adv Water Resour 14(1):31–41

    Article  Google Scholar 

  • Chang TJ, Kao HM, Chang KH, Hsu MH (2011) Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. J Hydrol 408(1):78–90

    Article  Google Scholar 

  • Chanson H (2009) Application of the method of characteristics to the dam break wave problem. J Hydraul Res 47(1):41–49

    Article  Google Scholar 

  • Chinnarasri C, Jirakitlerd S, Wongwises S (2004) Embankment dam breach and its outflow characteristics. Civ Eng Environ Syst 21(4):247–264

    Article  Google Scholar 

  • Costa JE (1985) Floods from dam failures, U.S. Geological Survey Open-File Rep, No. 85-560, U.S. Geological Survey Denver, Colorado

  • DHI (2014) MIKE-3, hydrodynamic and transport module scientific documentation. Danish Hydraulic Institute, New Delhi

    Google Scholar 

  • Dressler RF (1952) Hydraulic resistance effect upon the dam-break functions. J Res Nat Bur Stand 49(3):217–225

    Article  Google Scholar 

  • Dressler RF (1954) Comparison of theories and experiments for the hydraulic dam-break wave. Int As Sci Hydrol 38(3):319–328

    Google Scholar 

  • Dressler RF (1958) Unsteady non-linear waves in sloping channels. Proc R Soc Lond 247(1249):186–198

    Google Scholar 

  • Farhadi A, Mayrhofer A, Tritthart M, Glas M, Habersack H (2018) Accuracy and comparison of standard k–ϵ with two variants of k–ω turbulence models in fluvial applications. Eng Appl Comput Fluid 12(1):216–235

    Google Scholar 

  • Fernandez-Feria R (2006) Dam-break flow for arbitrary slopes of the bottom. J Eng Math 54(4):319–331

    Article  Google Scholar 

  • Fraccarollo L, Toro EF (1995) Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J Hydraul Res 33(6):843–864

    Article  Google Scholar 

  • Froehlich DC (1995) Peak outflow from breached embankment dam. J Fluid Mech 569(69):61–87

    Google Scholar 

  • Hogg AJ (2006) Lock-release gravity currents and dam-break flows. J Fluid Mech 569(69):61–87

    Article  Google Scholar 

  • Hooshyaripor F, Tahershamsi A (2015) Effect of reservoir side slopes on dam-break flood waves. Eng Appl Comput Fluid 9(1):458–468

    Google Scholar 

  • Hooshyaripor F, Tahershamsi A, Golian S (2014) Application of copula method and neural networks for predicting peak outflow from breached embankments. J Hydro Environ Res 8:292–303

    Article  Google Scholar 

  • Hou JM, Liang QH, Simons F, Hinkelmann R (2013) A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv Water Resour 52(2):107–131

    Article  Google Scholar 

  • Hou JM, Liang QH, Zhang BH, Hinkelmann R (2015) An efficient unstructured MUSCL scheme for solving the 2D shallow water equations. Environ Modell Softw 66(c):131–152

    Article  Google Scholar 

  • Hunt B (1982) Asymptotic solution for dam-break problems. J Hydraul Div 108(1):115–126

    Google Scholar 

  • Hunt B (1983) Asymptotic solution for dam break on sloping channel. J Hydraul Eng 109(12):1698–1706

    Article  Google Scholar 

  • Hunt B (1984) Perturbation solution for dam-break floods. J Hydraul Eng 110(8):1058–1071

    Article  Google Scholar 

  • Hunt B (1987) An inviscid dam-break solution. J Hydraul Res 1987(3):313–327

    Article  Google Scholar 

  • Kamrath P, Disse M, Hammer M, Köngeter J (2006) Assessment of discharge through a dike breach and simulation of flood wave propagation. Nat Hazards 38(1–2):63–78

    Article  Google Scholar 

  • Khankandi AF, Tahershamsi A, Soares-Frazão S (2012) Experimental investigation of reservoir geometry effect on dam-break flow. J Hydraul Res 50(4):376–387

    Article  Google Scholar 

  • Larocque LA, Imran J, Chaudhry MH (2013) Experimental and numerical investigations of two-dimensional dam-break flows. J Hydraul Eng 139(6):569–579

    Article  Google Scholar 

  • Lauber G, Hager WH (1998a) Experiments to dam-break wave: horizontal channel. J Hydraul Res 36(3):291–307

    Article  Google Scholar 

  • Lauber G, Hager WH (1998b) Experiments to dam-break wave: sloping channel. J Hydraul Res 36(5):761–773

    Article  Google Scholar 

  • Liang QH, Chen KC, Hou JM, Xiong T, Wang G, Qiang J (2016) Hydrodynamic modeling of flow impact on structures under extreme flow conditions. J Hydrodyn 28(2):267–274

    Article  Google Scholar 

  • Lobovsky L, Botia-Vera E, Castellana F, Mas-Soler J, Souto-Iglesias A (2014) Experimental investigation of dynamic pressure loads during dam break. J Fluid Struct 48:407–434

    Article  Google Scholar 

  • Mangeney A, Heinrich P, Roche R (2000) Analytical solution for testing debris avalanche numerical models. Pure Appl Geophys 157(6–8):1081–1096

    Article  Google Scholar 

  • Marsooli R, Wu W (2014) 3-D finite-volume model of dam-break flow over uneven beds based on VOF method. Adv Water Resour 70:104–117

    Article  Google Scholar 

  • Mohapatra PK, Bhallamudi SM (1996) Computation of a dam-break flood wave in channel transitions. Adv Water Resour 19(3):181–187

    Article  Google Scholar 

  • Oertel M, Bung DB (2012) Initial stage of two-dimensional dam-break waves: laboratory versus VOF. J Hydraul Res 50(1):89–97

    Article  Google Scholar 

  • Ozmen-Cagaty H, Kocaman S (2010) Dam-break flows during initial stage using SWE and RANS approaches. J Hydraul Res 48(5):603–611

    Article  Google Scholar 

  • Park IR, Kim KS, Kim J, Van SH (2012) Numerical investigation of the effects of turbulence intensity on dam-break flows. Ocean Eng 42(1):176–187

    Article  Google Scholar 

  • Pektas AO, Erdik T (2014) Peak discharge prediction due to embankment dam break by using sensitivity analysis based ANN. KSCE J Civ Eng 18(6):1868–1876

    Article  Google Scholar 

  • Peng M, Zhang LM (2012) Analysis of human risks due to dam-break floods—part 1: a new model based on Bayesian networks. Nat Hazards 64(1):903–933

    Article  Google Scholar 

  • Pilotti M, Tomirotti M, Valerio G (2010) Simplified method for the characterization of the hydrograph following a sudden partial dam break. J Hydraul Eng 136(10):693–704

    Article  Google Scholar 

  • Pilotti M, Tomirotti M, Valerio G, Milanesi L (2013) Discussion on experimental investigation of reservoir geometry effect on dam-break flow by A. Feizi Khankandi, A. Tahershamsi and S. Soares-Frazão. J Hydraul Res 51(2):220–222

    Article  Google Scholar 

  • Powledge G, Ralston DC, Miller P, Chen YH (1989) Mechanics of overflow erosion on embankments II. Hydraulic and design considerations. J Hydraul Eng 115(8):1056–1075

    Article  Google Scholar 

  • Ritter A (1892) Die Fortpflanzung der Wasserwellen (The propagation of water waves). Z Ver Dtsch Ing 36(33):947–954 (in German)

    Google Scholar 

  • Saberi O, Zenz G (2015) Empirical relationship for calculate outflow hydrograph of embankment dam failure due to overtopping flow. Int J Hydraul Eng 4(3):45–53

    Google Scholar 

  • Shigematsu T, Liu PLF, Oda K (2004) Numerical modeling of the initial stages of dam-break waves. J Hydraul Res 42(2):183–195

    Article  Google Scholar 

  • Stansby PK, Chegini A, Barnes TCD (1998) The initial stages of dam-break flow. J Fluid Mech 374(370):407–424

    Article  Google Scholar 

  • Stoker JJ (1957) Water waves: the mathematical theory with applications. Interscience Publishers, New York

    Google Scholar 

  • Stoker JJ (1959) Numerical solution of flood wave and river regulations problems. Proc Am Philos Soc 103(4):548–553

    Google Scholar 

  • Su ST, Barnes H (1970) Geometric and frictional effects on sudden releases. J Hydraul Div 96(11):2185–2200

    Google Scholar 

  • Taher-Shamsi A, Ponce VM, Shetty AV (2003) Embankment dam breaching: geometry and peak outflow characteristics. Dam Eng 14(2):73–82

    Google Scholar 

  • Tan ZH (1992) Analysis of dam break wave in a flat prismatic reservoir. J Hydraul Eng 4:39–47 (in Chinese)

    Google Scholar 

  • Wahl TL (2010) Dam breach modeling-an overview of analysis methods. In: Joint federal interagency conference on sedimentation and hydrologic modeling, Las Vegas, June

  • Walder JS, O’Connor JE (1997) Methods for predicting peak discharge of floods caused by failure of natural and constructed earth dams. Water Resour Res 33(10):2337–2348

    Article  Google Scholar 

  • Wang J, Liang D, Zhang J, Xiao Y (2016) Comparison between shallow water and Boussinesq models for predicting cascading dam-break flows. Nat Hazards 83(1):327–343

    Article  Google Scholar 

  • Waterways Experiment Station (WES) (1960) Floods resulting from suddenly breached dams. Misc paper no. 2-374. Rep 1: conditions of minimum resistance. Rep. Prepared for U.S. Army Corps of Engineers, Vicksburg

  • Whitham GB (1955) The effects of hydraulic resistance in the dam-break problem. Proc R Soc Lond 227A:399–407

    Google Scholar 

  • Xie RZ (1982) Computation for the discharge from the site of dam-break. Hydro Sci Eng 1:43–58 (in Chinese)

    Google Scholar 

  • Xie RZ (1989) Dam hydralics. Shangdong Science and Technology Press, Jinan (in Chinese)

    Google Scholar 

  • Xiong Y (2011) A dam break analysis using HEC-RAS. J Water Resour Prot 3(6):370–379

    Article  Google Scholar 

  • Xu F, Zhou H, Zhou J, Yang X (2012) A mathematical model for forecasting the dam-break flood routing process of a landslide dam. Math Probl Eng 2:857–868

    Google Scholar 

Download references

Acknowledgements

This research was supported financially by the State Key Laboratory Base of Eco-hydraulic Engineering in Arid Area, China (Grant No. 2017ZZKT-5), the National Natural Science Foundation of China (Grant No. 51609197), CAS “Light of West China” Program (Grant No. XAB2016AW06) and the Xian Science and Technology Program (Grant No. SF1335).

Author information

Authors and Affiliations

  1. State Key Laboratory Base of Eco-Hydraulic Engineering in Arid Area, School of Water Resources and Hydropower, Xi’an University of Technology, Xi’an, 710048, China

    Hui Hu, Jianfeng Zhang, Tao Li & Jie Yang

Authors
  1. Hui Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianfeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jie Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tao Li.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, H., Zhang, J., Li, T. et al. A simplified mathematical model for the dam-breach hydrograph for three reservoir geometries following a sudden full dam break. Nat Hazards 102, 1515–1540 (2020). https://doi.org/10.1007/s11069-020-03979-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11069-020-03979-w

Keywords

Search

Navigation