Skip to main content
SpringerLink
Log in

Shannon entropy maximization supplemented by neurocomputing to study the consequences of a severe weather phenomenon on some surface parameters

  • Original Paper
  • Published:
Natural Hazards Aims and scope Submit manuscript

Abstract

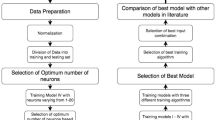
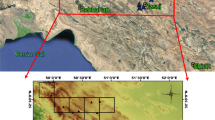
An information theoretic approach based on Shannon entropy is adopted in this study to discern the influence of pre-monsoon thunderstorm on some surface parameters. A few parameters associated with pre-monsoon thunderstorms over a part of east and northeast India are considered. Maximization of Shannon entropy is employed to test the relative contributions of these parameters in creating this weather phenomenon. It follows as a consequence of this information theoretic approach that surface temperature is the most important parameter among those considered. Finally, artificial neural network in the form of multilayer perceptron with backpropagation learning is attempted to develop predictive model for surface temperature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Abderrahim H, Reda Chellali M, Hamou A (2016) Forecasting PM10 in Algiers: efficacy of multilayer perceptron networks. Environ Sci Pollut Res 23:1634–1641

    Article  Google Scholar 

  • Brunsell NA (2010) A multiscale information theory approach to assess spatial-temporal variability of daily precipitation. J Hydrol 385:165–172

    Article  Google Scholar 

  • Chattopadhyay S (2007) Feed forward Artificial Neural Network model to predict the average summer-monsoon rainfall in India. Acta Geophys 55:369–382

    Article  Google Scholar 

  • Chattopadhyay S, Bandyopadhyay G (2008) Artificial neural network with backpropagation learning to predict mean monthly total ozone in Arosa, Switzerland. Int J Remote Sens 28:4471–4482. https://doi.org/10.1080/01431160701250440

    Article  Google Scholar 

  • Chattopadhyay G, Chattopadhyay S, Jain R (2010) Multivariate forecast of winter monsoon rainfall in India using SST anomaly as a predictor: Neurocomputing and statistical approaches. Comptes Rendus Geosci 342:755–765

    Article  Google Scholar 

  • Chaudhuri S (2006) Predictability of chaos inherent in the occurrence of severe thunderstorms. Adv Complex Syst 9:77–85

    Article  Google Scholar 

  • Chaudhuri S (2008) Preferred type of cloud in the genesis of severe thunderstorms—a soft computing approach. Atmos Res 88:149–156

    Article  Google Scholar 

  • Chaudhuri S, Chattopadhyay S (2003) Viewing the relative importance of some surface parameters associated with pre-monsoon thunderstorms through Ampliative Reasoning. Solstice: An Electronic Journal of Geography and Mathematics, Volume XIV, Number 1. Ann Arbor: Institute of Mathematical Geography, 2003. Persistent URL: http://hdl.handle.net/2027.42/60292

  • Chaudhuri S, Chattopadhyay S (2005) Neuro-computing based short range prediction of some meteorological parameters during the pre-monsoon season. Soft Comput 9:349–354

    Article  Google Scholar 

  • De SS, Bandyopadhyay B, Paul S (2011a) A neurocomputing approach to the forecasting of monthly maximum temperature over Kolkata, India using total ozone concentration as predictor. Comptes Rendus Geosci 343:664–676

    Article  Google Scholar 

  • De SS, De BK, Chattopadhyay G, Paul S, Haldar DK, Chakrabarty DK (2011b) Identification of the best architecture of a multilayer perceptron in modeling daily total ozone concentration over Kolkata, India. Acta Geophysica 59:361–376

    Article  Google Scholar 

  • Gardner MW, Dorling SR (1998) Artificial neural networks (the multilayer perceptron) a review of applications in the atmospheric sciences. Atmos Environ 32:2627–2636

    Article  Google Scholar 

  • Gray RM (1990) Entropy and information theory. Springer, New York

    Book  Google Scholar 

  • Gutierrez-Coreaa F-V, Manso-Callejo M-A, Moreno-Regidora M-P, Manrique-Sanchoa M-T (2016) Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Sol Energy 134:119–131

    Article  Google Scholar 

  • Hontoria L, Aguilera J, Zufiria P (2005) An application of the multilayer perceptron: solar radiation maps in Spain. Sol Energy 79:523–530

    Article  Google Scholar 

  • Hsieh WW, Tang B (1998) Applying neural network models to prediction and data analysis in meteorology and oceanography. Bull Am Meteorol Soc 79:1855–1870

    Article  Google Scholar 

  • Kawachi T, Maruyama T, Singh VP (2001) Rainfall entropy for delineation of water resources zones in Japan. J Hydrol 246:36–44

    Article  Google Scholar 

  • Klir GJ, Folger TA (2009) Fuzzy-sets. Uncertainty and information. Prentice-Hall, New Jersey

    Google Scholar 

  • Koutsoyiannis D, Pachakis D (1996) Deterministic chaos versus stochasticity in analysis and modeling of point rainfall series. J Geophys Res Atmos 101(D21):26441–26451. https://doi.org/10.1029/96JD01389

    Article  Google Scholar 

  • Lesne A (2014) Shannon entropy: a rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics. Math Struct Comp Sci 24:e240311. https://doi.org/10.1017/S0960129512000783

    Article  Google Scholar 

  • Litta AJ, Idicula SM, Mohanty UC (2013) Artificial neural network model in prediction of meteorological parameters during premonsoon thunderstorms. Int J Atmos Sci, (2013), Article ID 525383, 14 p

  • Liu Y, Liu C, Wang D (2011) Understanding atmospheric behaviour in terms of entropy: a review of applications of the second law of thermodynamics to meteorology. Entropy 13:211–240. https://doi.org/10.3390/e13010211

    Article  Google Scholar 

  • Michael S, Koutsoyiannis PD (2012) Entropy based derivation of probability distributions: a case study to daily rainfall. Adv Water Resour 45:51–57

    Article  Google Scholar 

  • Nagendra SMS, Khare M (2006) Artificial neural network approach for modelling nitrogen dioxide dispersion from vehicular exhaust emissions. Ecol Model 190:99–115

    Article  Google Scholar 

  • Nebot A, Mugica V, Escobet A (2008) Ozone prediction based on meteorological variables: a fuzzy inductive reasoning approach. Atmos Chem Phys Discuss 8:12343–12370

    Article  Google Scholar 

  • Özbaya B, Aydin G, Senay K, Dogruparmaka şÇ, Ayberka S (2011) Predicting tropospheric ozone concentrations in different temporal scales by using multilayer perceptron models. Ecological Informatics 6:242–247

  • Palmer TN (2000) Predicting uncertainty in forecats of weather and climate. Rep Prog Phys 63:71–116

    Article  Google Scholar 

  • Perez P, Reyes J (2002) Prediction of maximum of 24-h average of PM10 concentrations 30h in advance in Santiago, Chile. Atmos Environ 36:4555–4561

    Article  Google Scholar 

  • Perez P, Trier A, Reyes J (2000) Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile. Atmos Environ 34:1189–1196

    Article  Google Scholar 

  • Richardson DS (2000) Skill and relative economic value of the ECMWF ensemble prediction system. Q J R Meteorol Soc. 126:649–667

    Article  Google Scholar 

  • Roulston MS, Smith LA (2002) Evaluating probabilistic forecats using information theory. Mon Weather Rev 130:1653–1660

    Article  Google Scholar 

  • Sivakumar B (2017) Chaos in hydrology: bridging determinism and stochasticity, 1st edn. Springer, Berlin

    Book  Google Scholar 

  • Varotsos C (2007) Power-law correlations in column ozone over Antarctica. Int J Remote Sens 27:3333–3342

    Google Scholar 

  • Varotsos CA, Efstathiou MN, Cracknell AP (2013) Plausible reasons for the inconsistencies between the modeled and observed temperatures in the tropical troposphere. Geophys Res Lett 40:4906–4910

    Article  Google Scholar 

  • Varotsos CA, Tzanis C, Cracknell AP (2016b) Precursory signals of the major El Niño Southern Oscillation events. Theoret Appl Climatol 124:903–912

    Article  Google Scholar 

  • Varotsos C, Tzanis C, Efstathiou M, Deligiorgi D (2015) Tempting long-memory in the historic surface ozone concentrations at Athens, Greece. Atmos Pollut Res 6:1055–1057

    Article  Google Scholar 

  • Varotsos CA, Tzanis CG, Sarlis NV (2016) On the progress of the 2015–2016 El Niño event. Atmos Chem Phys 16:2007–2011

    Article  Google Scholar 

  • Varotsos CA, Sarlis NV, Efstathiou M (2017) On the association between the recent episode of the quasi-biennial oscillation and the strong El Niño event. Theoretical and Applied Climatology, On-line first, https://doi.org/10.1007/s00704-017-2191-9

  • Willmott CJ (1982) Some comments on the evaluation of model performance. Bull Am Meteorol Soc 63:1309–1313

    Article  Google Scholar 

  • Xiao R, Chandrasekar V (1997) Development of a neural network based algorithm for rainfall estimation from radar observations. IEEE Trans Geosci Remote Sens 35:160–171

    Article  Google Scholar 

  • Xu Q (2007) Measuring information content from observations for data assimilation: relative entropy versus shannon entropy difference. Tellus A Dyn Meteorol Oceanogr 59:198–209. https://doi.org/10.1111/j.1600-0870.2006.00222.x

    Article  Google Scholar 

  • Zeng X, Pielke RA, Eykholt R (1993) Chaos theory and its applications to the atmosphere. Bull Am Meteorol Soc 74:631–644

    Article  Google Scholar 

Download references

Acknowledgements

Sincere thanks are due to the anonymous reviewers for their thoughtful suggestions. Financial support from DST, Govt. of India, under Project Grant No. SR/WOS-A/EA-10/2017(G) is thankfully acknowledged by Goutami Chattopadhyay. Authors Surajit Chattopadhyay and Goutami Chattopadhyay are thankful to IUCAA, Pune, India, for the hospitality.

Author information

Authors and Affiliations

  1. Department of Mathematics, Amity University, Major Arterial Road, Action Area II, Rajarhat, New Town, Kolkata, 700135, India

    Surajit Chattopadhyay

  2. Department of Atmospheric Sciences, University of Calcutta, 51/2 Hazra Road, Kolkata, 700019, India

    Goutami Chattopadhyay & Subrata Kumar Midya

Authors
  1. Surajit Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Goutami Chattopadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Subrata Kumar Midya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Surajit Chattopadhyay.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chattopadhyay, S., Chattopadhyay, G. & Midya, S.K. Shannon entropy maximization supplemented by neurocomputing to study the consequences of a severe weather phenomenon on some surface parameters. Nat Hazards 93, 237–247 (2018). https://doi.org/10.1007/s11069-018-3298-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11069-018-3298-8

Keywords

Search

Navigation