Abstract
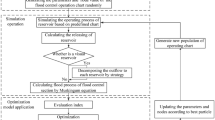
As the large-scale cascaded reservoirs have been developed rapidly in recent years, river basin flood control (RBFC) has become a complex, multi-objective and multi-reservoir problem. In order to realize the optimal operation and management of reservoirs in mainstreams and branches, this paper presents a generalized multi-objective flood control model (MOFCM) for joint optimal dispatching of cascade reservoirs, which is applied to cascade reservoirs in lower reaches of Jinsha River and Three Gorges Reservoir in Yangtze River (JFCR–TGR). Meanwhile, a multi-objective cultural self-adaptive electromagnetism-like mechanism (MOSEM) algorithm is introduced to solve RBFC problem. In the case study, comparing with the natural runoff of the Chuan River, the maximum release of optimal schemes is lesser, its reduced range is from 1727 to 12,887 m3/s and the flood peak deduction rate is from 6.4 to 48 %. Results of case studies demonstrate that MOFCM is practicable and efficient for multipurpose multi-reservoir flood control. The optimal operation schemes obtained by MOSEM in JFCR–TGR system can be used to assist the decision makers in choosing the most efficient scheme. Furthermore, MOFCM can accomplish multiple-object optimization effectively under various scheduling situations.






Similar content being viewed by others
References
Alikhani MG, Javadian N, Tavakkoli-Moghaddam R (2009) A novel hybrid approach combining electromagnetism-like method with Solis and Wets local search for continuous optimization problems. J. Glob. Optim 44(2):227–234
Birbil SI, Fang SC (2003) An electromagnetism-like mechanism for global optimization. J. Glob. Optim 25(3):263–282
Birbil SI, Fang SC, Sheu RL (2004) On the convergence of a population-based global optimization algorithm. J. Glob. Optim 30(2–3):301–318
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Goor Q, Kelman R, Tilmant A (2011) Optimal multipurpose-multireservoir operation model with variable productivity of hydropower plants. J Water Res Pl-Asce 137(3):258–267
Jood M, Dashti M, Abrishamchi A (2012) A system dynamics model for improving flood control operation policies, World Environmental and Water Resources Congress 2012, pp 962–972
Knox JC (2000) Sensitivity of modern and Holocene floods to climate change. Quat Sci Rev 19(1–5):439–457
Kumar DN, Baliarsingh F, Raju KS (2010) Optimal reservoir operation for flood control using folded dynamic programming. Water Resour Manag 24(6):1045–1064
Li YH, Zhou JZ, Zhang YC, Qin H, Liu L (2010) Novel multiobjective shuffled frog leaping algorithm with application to reservoir flood control operation. J Water Resour Plan Manag 136(2):217–226. http://ascelibrary.org/doi/abs/10.1061/(ASCE)WR.1943-5452.0000027
Marien JL, Damázio JM, Costa FS (1994) Building flood control rule curves for multipurpose multireservoir systems using controllability conditions. Water Resour Res 30(4):1135–1144
Needham J, Watkins D Jr, Lund J, Nanda S (2000) Linear programming for flood control in the Iowa and Des Moines Rivers. J Water Resour Plan Manag 126(3):118–127
Qian WY, Li A (2008) Adaptive differential evolution algorithm for multiobjective optimization problems. Appl Math Comput 201(1–2):431–440
Qin H, Zhou JZ, Lu YL, Li YH, Zhang YC (2010) Multi-objective cultured differential evolution for generating optimal trade-offs in reservoir flood control operation. Water Resour Manag 24(11):2611–2632
Reynolds RG (1994) An introduction to cultural algorithms. In: Proceedings of the third annual conference on evolutionary programming. Singapore, pp 131–139
Saleem SM (2001) Knowledge-based solution to dynamic optimization problems using cultural algorithms, Wayne State University, 286 pp
Tsou CS (2009) Evolutionary Pareto optimizers for continuous review stochastic inventory systems. Eur J Oper Res 195(2):364–371
Tsou CS, Kao CH (2006) An electromagnetism-like meta-heuristic for multi-objective optimization. In IEEE congress on evolutionary computation, CEC 2006 (pp. 1172-1178). New York, IEEE
Tsou CS, Kao CH (2008) Multi-objective inventory control using electromagnetism-like meta-heuristic. Int J Prod Res 46(14):3859–3874
Wang XJ, Zhao RH, Hao YW (2011) Flood control operations based on the theory of variable fuzzy sets. Water Resour Manag 25(3):777–792
Ward FA (2012) Cost-benefit and water resources policy: a survey. Water Policy 14(2):250–280
Wasimi SA, Kitanidis PK (1983) Real-time forecasting and daily operation of a multireservoir system during floods by linear quadratic Gaussian control. Water Resour Res 19(6):1511–1522
Wei C-C, Hsu N-S (2008) Multireservoir real-time operations for flood control using balanced water level index method. J Environ Manag 88(4):1624–1639
Wei CC, Hsu NS (2009) Optimal tree-based release rules for real-time flood control operations on a multipurpose multireservoir system. J Hydrol 365(3–4):213–224
Windsor JS (1973) Optimization model for the operation of flood control systems. Water Resour Res 9(5):1219–1226
Yazdi J, Neyshabouri S (2012) Optimal design of flood-control multi-reservoir system on a watershed scale. Nat Hazards 63(2):629–646
Zhang R, Zhou JZ, Wang YQ (2012) Multi-objective optimization of hydrothermal energy system considering economic and environmental aspects. Int J Electr Power Energy Syst 42(1):384–395
Zitzler E, Laumanns M, Thiele L (2001) SPEA2: improving the strength pareto evolutionary algorithm, Eidgenössische Technische Hochschule Zürich (ETH)
Acknowledgments
This study is financially supported by the basic research funds of central public welfare research institutes of China (numbers CKSF2013011/SZ and CKSF2013010/SZ).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, Q., Ouyang, S. Research on multi-objective joint optimal flood control model for cascade reservoirs in river basin system. Nat Hazards 77, 2097–2115 (2015). https://doi.org/10.1007/s11069-015-1692-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11069-015-1692-z