Skip to main content
SpringerLink
Log in

An investigation on the predictability of thunderstorms over Kolkata, India using fuzzy inference system and graph connectivity

  • Original Paper
  • Published:
Natural Hazards Aims and scope Submit manuscript

Abstract

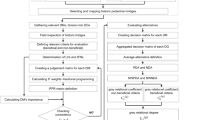
The purpose of this study was to develop a computing system (CS) with fuzzy membership and graph connectivity approach to estimate the predictability of thunderstorms during the pre-monsoon season (April–May) over Kolkata (22°32′N, 88°20′E), India. The stability indices are taken to form the inputs of the CS. Ten important stability indices are selected to prepare the input of the fuzzy set. The data analysis during the period from 1997 to 2006 led to identify the ranges of the stability indices through membership function for preparing the fuzzy inputs. The possibility of thunderstorms with the given ranges of the stability indices is validated with the bipartite graph connectivity method. The bipartite graphs are prepared with two sets of vertices, one set for three membership functions (strong, moderate and weak) with the stability indices and the other set includes the three membership functions for the probability of thunderstorms (high, medium and low). The percentages of degree of vertex (ΔG) are computed from a sample set of bipartite graph on thunderstorm days and are assigned as the measure of the likelihood of thunderstorms. The results obtained from graph connectivity analysis are found to be in conformity with the output of fuzzy interface system (FIS). The result reveals that the skill of graph connectivity is better and supports the FIS in estimating the predictability of thunderstorms over Kolkata during the pre-monsoon season. The result further reveals from the minimum degree of vertex connectivity that among the ten selected stability indices, only four indices: lifted index, bulk Richardson number, Boyden index and convective available potential energy, are most relevant for estimating the predictability of thunderstorms over Kolkata, India.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Abraham A, Philip NS, Joseph B (2001) Will we have a wet summer? Long term rain forecasting using soft computing models. In: Kerchoffs EJH SnorekM (ed) Modeling and simulation 2001, publication of the society for computer simulation international. Czech Republic, Prague, pp 1044–1048

    Google Scholar 

  • Anderson T, Anderson M, Jacobson C, Nilsson S (1989) Thermodynamic indices for forecasting thunderstorms in southern Sweden. Meteorol Mag 118:141–146

    Google Scholar 

  • Anthes RA (1976) Numerical prediction of severe storms—certainty, probability, or dream. Bull Amer Met Soc 57:423–430

    Google Scholar 

  • Basak P, Sarkar D and Mukhopadhyay AK (2012) Estimation of thunderstorm days from the radio-sonde observations at Kolkata (22.53oN, 88.33oE), India during pre-monsoon season: an ANN based approach earth science India, eISSN: 0974–8350 Vol. 5 (IV), October, 2012, pp. 139–151

  • Bluestein HB, Parker SS (1993) Modes of isolated, severe convective storm formation along the dryline. Mon Wea Rev 121:1354–1372

  • Chaudhuri S (2005) Genetic algorithm to recognize apt energy for the genesis of severe thunderstorms. Vatabaran AFAC J Meteorol 29(2):1–8

    Google Scholar 

  • Chaudhuri S (2006a) Predictability of chaos inherent in the occurrence of severe thunderstorms. Adv Complex Sys 9:1–9

    Article  Google Scholar 

  • Chaudhuri S (2006b) A hybrid model to estimate the depth of potential convective instability during severe thunderstorms. Soft Comput 10:243–248

    Article  Google Scholar 

  • Chaudhuri S (2007) Chaotic graph theory approach for identification of convective available potential energy (CAPE) patterns required for the genesis of severe thunderstorm. Adv Complex Sys 10:413–422

    Article  Google Scholar 

  • Chaudhuri S (2008a) Identification of the level of downdraft formation during severe thunderstorms: a frequency domain analysis. Meteorol Atmos Phys 102:123–129

    Article  Google Scholar 

  • Chaudhuri S (2008b) Preferred type of cloud in the genesis of severe thunderstorms—a soft computing approach. Atmos Res 88:149–156

    Article  Google Scholar 

  • Chaudhuri S (2010) Convective energies in forecasting severe thunderstorms with one hidden layer neural net and variable learning rate back propagation algorithm. Asia-Pacific. J Atmos Sci 46(2):173–183

    Google Scholar 

  • Chaudhuri S (2011) Implementation of intuitionistic fuzzy logic to assess the predictability of severe thunderstorms. Asia-Pacific J Atmos Sci 47(5):477–483

    Article  Google Scholar 

  • Chaudhuri S, Das D and Middey A An investigation on the predictability of thunderstorms over Kolkata, India using fuzzy inference system and graph connectivity” (present study)

  • Chaudhuri S, Middey A (2009) Applicability of bipartite graph model for thunderstorms forecast over Kolkata. Adv Meteorol 2009:1–12

    Article  Google Scholar 

  • Chaudhuri S, Middey A (2011a) Nowcasting thunderstorms with graph spectral distance and entropy estimation. Meteorol Appl 18(2):238–249

    Article  Google Scholar 

  • Chaudhuri S, Middey A (2011b) Adaptive neuro-fuzzy inference system to forecast peak gust speed during thunderstorms. Meteorol Atmos Phys 14:139–149

    Article  Google Scholar 

  • Chaudhuri S, Middey A (2012) Disparity in the characteristic of thunderstorms and associated lightning activities over dissimilar terrains. Meteorol Atmos Phys 119(3–4):151–161

    Google Scholar 

  • Chaudhuri S, Middey A (2013) Comparison of tropical and midlatitude thunderstorm characteristics anchored in thermodynamic and dynamic aspects. Asia-Pacific J Atmos Sci doi: 10.1007/s13143-014-0006-9

  • Chaudhuri S, Pal J, Middey A and Goswami S (2013) Nowcasting Bordoichila with a composite stability index. Natural Hazards (Springer), 66, 2, 591–607 (IF:1.529)

  • Chaudhuri S, Goswami S and Middey A (2014) Morphological classification pertaining to validate the climatology and category of thunderstorms over Kolkata, India theoretical and applied climatology (Springer), 116, 1–2, 61–74

  • Chung F (1992) Spectral graph theory. CBMS Regional Conference Series in Mathematics 92. American Mathematical Society, Providence RI

  • Comric AC (1997) Comparing neural networks and regression models for ozone forecasting. J Air Waste Manag As 47:653–663

    Article  Google Scholar 

  • Dance S, Ebert E, Scurrah D (2010) Thunderstorm strike probability nowcasting. J Atmos Oceanic Technol 27:79–93

    Article  Google Scholar 

  • Diestel R (2005) Graph theory. Springer, New York

    Google Scholar 

  • Djuric D (1994) Weather analysis ISBN-10: 0135011493|ISBN-13: 9780135011492

  • Doswell CA (1987) The distinction between large-scale and mesoscale contribution to severe convection: a case study example. Weather Forecast 2:3–16

    Article  Google Scholar 

  • El-Ghoul M (2002) The most general set and chaos graph, chaos. Solitons Fractals UK 18:833–838

    Article  Google Scholar 

  • Huntrieser H, Schiesser HH, Schmid W, Waldvogel A (1997) Comparison of traditional and newly developed thunderstorm indices for Switzerland. Weather Forecast 12:108–125

    Article  Google Scholar 

  • Jacovides CP, Yonetani T (1990) An evaluation of stability indices for thunderstorm prediction in greater Cyprus. Weather Forecast 5(4):559–569

    Article  Google Scholar 

  • Lakshmanan V, Witt A (1997) A fuzzy logic approach to detecting severe updrafts, A.I. Applications 11:1–12

    Google Scholar 

  • Lee RR, Passner JE (1993) The development and verification of TIPS: an expert system to forecast thunderstorm occurrence. Weather Forecast 8:271–280

    Article  Google Scholar 

  • Lilly DK (1990) Numerical prediction of thunderstorms—has its time come? Quart J Roy Meteorol Soc 116:779–798

    Google Scholar 

  • Lin Pin-Fang, Chang Pao-Liang, Jou Ben Jong-Dao, Wilson James W, Roberts Rita D (2012) Objective prediction of warm season afternoon thunderstorms in Northern Taiwan using a fuzzy logic approach. Weather Forecast 27:1178–1197

    Article  Google Scholar 

  • Litta AJ, Mary Idicula S and Mohanty UC (2013) Artificial neural network model in prediction of meteorological parameters during pre monsoon thunderstorms international journal of atmospheric sciences, 2013 (2013), Article ID 525383, 14 page http://dx.doi.org/10.1155/2013/525383MAE 19.61

  • Lorenz EN (1963) Deterministic nonperiodic flow. J Atmos Sci 20:130–141

    Article  Google Scholar 

  • Lorenz EN (1969) Three approaches to atmospheric predictability. Bull Amer Meteorol Soc 50:345–351

    Google Scholar 

  • Marzban C, Witt A (2001) A Bayesian neural network for severe-hail size prediction. Weather Forecast 16(5):600–610

    Article  Google Scholar 

  • Mull S, Rao YP (1950) On the origin of down draughts in a thunder-storm. Indian J Meteorol Geophys 1:171

    Google Scholar 

  • Murtha J (1995) Applications of fuzzy logic in operational meteorology. Scientific Services and Professional Development Newsletter, Canadian Forces Weather Service, pp 42–54

    Google Scholar 

  • Neumann CJ (1971) The thunderstorm forecasting system at the Kennedy Space Center. J Appl Meteorol 10:921–936

    Article  Google Scholar 

  • Orlanski I (1975) A rational subdivision of scales for atmospheric processes. Bull Am Meteorol Soc 56(5):527–530

    Google Scholar 

  • Pokrovsky OM, Kwok RHF, Ng CN (2002) Fuzzy logic approach for description of meteorological impacts on urban air pollution species: a Hong Kong case study. Comput Geosci 28(1):119–127

    Article  Google Scholar 

  • Rasmussen EN, Blanchard DO (1998) A baseline climatology of sounding-derived supercell and tornado forecast parameters. Weather Forecast 13:1148–1164

    Article  Google Scholar 

  • Reap RM, Foster DS (1979) Automated 12–36 hour probability forecasts of thunderstorms and severe local storms. J Appl Meteorol 18:1304–1315

    Article  Google Scholar 

  • Schultz P (1989) Relationship of several stability indices to convective weather events in Northest Colorado. Weather Forecast 4:73–80

    Article  Google Scholar 

  • Stone HM (1985) A comparison among various thermodynamic parameters for the prediction of convective activity, Part I, NOAA Technical Memorandum, NWS-ER 68, Washington DC

Download references

Acknowledgments

The authors acknowledge India Meteorological Department (IMD) for making data/records available for the present research. The authors thank the anonymous reviewers for their valuable comments and suggestion which helped to improve the clarity of the paper.

Author information

Author notes

  1. Anirban Middey

    Present address: Air Pollution Control Division, National Environmental Engineering Research Institute, Nehru Marg, Nagpur, 440020, India

Authors and Affiliations

  1. Department of Atmospheric Sciences, University of Calcutta, 51/2 Hazra Road, Kolkata, 700 019, India

    Sutapa Chaudhuri, Debanjana Das & Anirban Middey

Authors
  1. Sutapa Chaudhuri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Debanjana Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anirban Middey
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sutapa Chaudhuri.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chaudhuri, S., Das, D. & Middey, A. An investigation on the predictability of thunderstorms over Kolkata, India using fuzzy inference system and graph connectivity. Nat Hazards 76, 63–81 (2015). https://doi.org/10.1007/s11069-014-1477-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11069-014-1477-9

Keywords

Search

Navigation