Prediction of the run-out distance of the debris flow based on the velocity attenuation coefficient

Abstract

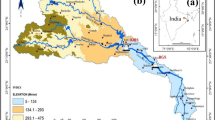
Our aim is to determine the run-out distance of the debris flow that is crucial in the assessment, prevention and control of the debris flow hazard. Based on the variation characteristic of debris flow velocity in the alluvial fan, this paper proposes the calculation method of the velocity attenuation coefficient of the debris flow. By defining the velocity attenuation coefficient and deducing its calculating formula, this paper puts forward a new method to determine the run-out distance of the debris flow based on the velocity attenuation coefficient, and Gangou debris flow in Luding County, Sichuan Province is selected as a case for calculation and verification. Having 10 m as its measuring spacing, this paper measured 19 sections at the alluvial fan of the Gangou debris flow (among them, 11 sets of data are valid). And based on the measurement, this paper analyzes the characteristic of the velocity attenuation and calculates its velocity attenuation coefficient after the 2005 debris flow. The study indicates that when the velocity of Gangou debris flow at the alluvial fan is greater than 12 % of the initial velocity (at the mouth of gully), the attenuation is quite remarkable. But when the velocity at the alluvial fan is less than 12 % of the initial velocity, the attenuation is quite slow. Besides, when Gangou debris flow rushes out of the gully mouth (the initial velocity is 10 m/s) and when it attenuates to the 32 time, its velocity is less than 0.1 m/s, the debris flow is considered to stop flowing, and the run-out distance of Gangou debris flow is calculated to be 320 m. But the present alluvial fan of Gangou debris flow is measured to be 285 m in length, and the calculated run-out distance is 320 m, which is 35 m longer than its present length. This means when the debris flow runs out in 2005, it blocked up the main river (Dadu River) in some extent. And this finding is generally in accordance with that from the field survey. The findings can be of theoretical and practical significance in the debris flow hazard assessment, as well as its prevention and mitigation.