Skip to main content
SpringerLink
Log in

Planar Location and Design of a New Facility with Inner and Outer Competition: An Interval Lexicographical-like Solution Procedure

  • Published:
Networks and Spatial Economics Aims and scope Submit manuscript

Abstract

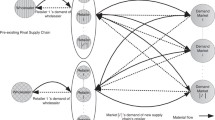
A chain has to decide the location and design for a single new facility in a region where a set of facilities already exists offering the same type of product. Some of the existing facilities belong to the chain and the others are competitors. Since competition comes from outside the chain, the maximization of the profit is the main objective of the chain’s owner. Customers are supposed to patronize all the facilities, the old and the new, proportionally to the attraction they feel for them. The entrance of the new facility may thus also have a detrimental effect on the market shares of the existing chain-owned facilities, and this cannibalization should be minimized as a secondary objective. This problem is formulated as a biobjective optimization problem, and a variant of the lexicographic method is proposed to generate certain efficient solutions. This requires solving two related optimization problems, both neither convex nor concave, for which a unified interval branch and bound method is developed. Computational experiments on randomly generated problems show the feasibility of the approach, while an application of the model with real data demonstrates its use for economical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Achabal D, Gorr WL, Mahajan V (1982) MULTILOC: a multiple store location model. J Retail 58:5–25

    Google Scholar 

  • Centro Regional de Estadística de Murcia (2003) Anuario estadístico de la Región de Murcia : Dirección General de Economía, Planificación y Estadística, Centro Regional de Estadística de Murcia (2003)

  • Colomé R, Serra D (2001) Consumer choice and optimal location models: formulations and heuristics. Pap Reg Sci 80:439–464

    Article  Google Scholar 

  • Current JR, Storbeck JE (1994) A multiobjective approach to design franchise outlet networks. J Oper Res Soc 45:71–81

    Article  Google Scholar 

  • Drezner T (1994a) Locating a single new facility among existing, unequally attractive facilities. J Reg Sci 34:237–252

    Article  Google Scholar 

  • Drezner T (1994b) Optimal continuous location of a retail facility, facility attractiveness, and market share: an interactive model. J Retail 70:49–64

    Article  Google Scholar 

  • Drezner T, Drezner Z (2004) Finding the optimal solution to the Huff based competitive location model. Comput Manage Sci 1:193–208

    Article  Google Scholar 

  • Drezner T, Drezner Z, Salhi S (2002) Solving the multiple competitive facility location problem. Eur J Oper Res 142:138–151

    Article  Google Scholar 

  • Drezner Z (ed) (1995) Facility Location: A Survey of Applications and Methods. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Eiselt HA, Laporte G, Thisse J-F (1993) Competitive location models: a framework and bibliography. Transp Sci 27:44–54

    Google Scholar 

  • Ehrgott M (2005) Multicriteria Optimization, 2nd edn. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Fernández J, Fernández P, Pelegrín B (2000) A continuous location model for siting a non-noxious undesirable facility within a geographical region. Eur J Oper Res 121:259–274

    Article  Google Scholar 

  • Fernández J, Fernández P, Pelegrín B (2002) Estimating actual distances by norm functions: a comparison between the l k,p,θ -norm and the \(l_{b_1,b_2,\theta}\)-norm and a study about the selection of the data set. Comput Oper Res 29:609–623

    Article  Google Scholar 

  • Fernández J, Pelegrín B (2000) Sensitivity analysis in continuous location models via interval analysis. Stud Locat Anal 14:121–136

    Google Scholar 

  • Fernández J, Pelegrín B (2001) Using interval analysis for solving planar single-facility location problems: new discarding tests. J Glob Optim 19:61–81

    Article  Google Scholar 

  • Fernández J, Pelegrín B, Plastria F, Tóth B (2005) Solving a Huff-like competitive location and design model for profit maximization in the plane. Eur J Oper Res DOI: 10.1016/j.ejor.2006.02.005. (to appear)

  • Fernández J, Pelegrín B, Plastria F, Tóth B (2004) Sensitivity of optimal solutions to a Huff-type competitive location and design problem (Working paper)

  • Fernández J, Tóth B, Plastria F, Pelegrín B (2006) Reconciling franchisor and franchisee: a planar biobjective competitive location and design model. In: Recent Advances in Optimization. Lectures Notes in Economics and Mathematical Systems vol. 563. Springer, Berlin Heidelberg New York, pp375–398

    Google Scholar 

  • Fishburn PC (1974) Lexicographic orders, utilities and decision rules: a survey. Manage Sci 20:1442–1471

    Article  Google Scholar 

  • Friesz TL, Miller T, Tobin RL (1988) Competitive networks facility location models: a survey. Pap Reg Sci Assoc 65:47–57

    Google Scholar 

  • Ghosh A, Craig CS (1991) FRANSYS: a franchise distribution system location model. J Retail 67:466–495

    Google Scholar 

  • Hammer R, Hocks M, Kulisch U, Ratz D (1995) C++ Toolbox for Verified Computing. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Hansen E (1992) Global Optimization Using Interval Analysis. Marcel Dekker, New York

    Google Scholar 

  • Hansen P, Jaumard B (1995) Lipschitz optimization. In: Handbook of Global Optimization. Kluwer, Dordrecht, The Netherlands, pp407–494

    Google Scholar 

  • Hansen P, Jaumard B, Tuy H (1995) Global optimization in location. In: Facility Location: A Survey of Applications and Methods. Springer, Berlin Heidelberg New York, pp 43–68

    Google Scholar 

  • Hodgson MJ (1981) A location-allocation model maximizing consumers’ welfare. Reg Stud 15:493–506

    Article  Google Scholar 

  • Huff DL (1964) Defining and estimating a trading area. J Mark 28:34–38

    Article  Google Scholar 

  • Huff DL (1966) A programmed solution for approximating an optimum reail location. Land Econ 42:293–303

    Article  Google Scholar 

  • Jain AK, Mahajan V (1979) Evaluating the competitive environment in retailing using multiplicative competitive interactive models. In: Sheth J (ed) Research in Marketing. JAI Press, Greenwich, Connecticut, pp 217–235

    Google Scholar 

  • Kearfott RB (1996) Rigorous Global Search: Continuous Problems. Kluwer, Dordrecht, The Netherlands

    Google Scholar 

  • Kearfott RB, Nakao MT, Neumaier A, Rump SM, Shary SP, van Hentenryck P (2002) Standardized notation in interval analysis. Reliab Comput. Submitted for publication, available at http://www.mat.univie.ac.at/~neum/software/int/

  • Kilkenny M, Thisse JF (1999) Economics of location: a selective survey. Comput Oper Res 26:1369–1394

    Article  Google Scholar 

  • Knüppel O (1994) PROFIL/BIAS—a fast interval library. Comput 53:277–287

    Article  Google Scholar 

  • Markót MC, Fernández J, Casado LG, Csendes T (2006) New interval methods for constrained global optimization. Math Prog Ser A 106:287–318

    Article  Google Scholar 

  • Martínez JA, Casado LG, García I, Tóth B, AMIGO: Advanced Multidimensional Interval analysis Global Optimization algorithm. In: Frontiers in Global Optimization. Nonconvex Optimization and its Applications, vol. 74. Kluwer, pp313–326 (2003)

  • Miettinen KS (1998) Nonlinear multiobjective optimization. Kluwer, Boston, Massachusetts

    Google Scholar 

  • Miller TC, Friez TL, Tobin RL (1996) Equilibrium Facility Location on Networks. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Nakanishi M, Cooper LG (1974) Parameter estimate for mutiplicative interactive choice model: least square approach. J Mark Res 11:303–311

    Article  Google Scholar 

  • Peeters PH, Plastria F (1992) Discretization results for the Huff and Pareto–Huff competitive location models on networks. Top 6:247–260

    Google Scholar 

  • Plastria F (1992) GBSSS: the generalized big square small square method for planar single-facility location. Eur J Oper Res 62:163–174

    Article  Google Scholar 

  • Plastria F (2001) Static competitive facility location: an overview of optimisation approaches. Eur J Oper Res 129:461–470

    Article  Google Scholar 

  • Plastria F (2005) Avoiding cannibalization and/or competitor reaction in planar single facility location. J Oper Res Soc Jpn 48:148–157

    Google Scholar 

  • Ratschek H, Rokne J (1984) Computer Methods for the Range of Functions. Ellis Horwood, Chichester, UK

    Google Scholar 

  • Ratschek H, Rokne J (1988) New Computer Methods for Global Optimization. Ellis Horwood, Chichester, UK

    Google Scholar 

  • Schmalensee R, Thisse JF (1988) Perceptual maps and the optimal location of new products: an integrative essay. Int J Res Mark 5:225–249

    Article  Google Scholar 

  • Suarez-Vega R, Santos-Peñate DR, Dorta-González P (2004) Discretization and resolution of the (r/X p ) medianoid problem involving quality criteria. Top 12:111–133

    Google Scholar 

  • Tóth B, Csendes T (2005) Empirical investigation of the convergence speed of inclusion functions. Reliab Comput 11:253–273

    Article  Google Scholar 

  • Tóth B, Fernández J, Csendes T (2007) Empirical convergence speed of inclusion functions for facility location problems. J Comput Appl Math 199:384–389 DOI:10.1016/j.cam.2005.07.037

    Google Scholar 

  • Visual GIS Engineering (2003) VisualMap. Basauri 17 (La Florida) 28023 Madrid

  • Wendell RE, McKelvey RD (1981) New perspectives in competitive location theory. Eur J Oper Res 6:174–182

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Facultad de Matemáticas, Universidad de Murcia, 30100 Espinardo, Murcia, Spain

    José Fernández

  2. Department of Statistics and Operations Research, University of Murcia, Murcia, Spain

    José Fernández, Blas Pelegrín & Boglárka Tóth

  3. MOSI-Department of Mathematics, Operations Research and Information Systems for Management, Vrije Universiteit Brussel, Brussels, Belgium

    Frank Plastria

Authors
  1. José Fernández
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Blas Pelegrín
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Frank Plastria
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Boglárka Tóth
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to José Fernández.

Additional information

This paper has been supported by the Ministry of Education and Science of Spain under the research project SEJ2005-06273/ECON, in part financed by the European Regional Development Fund (ERDF).

Boglárka Tóth, on leave from the Research Group on Artificial Intelligence of the Hungarian Academy of Sciences and the University of Szeged, H-6720 Szeged, Aradi vértanúk tere 1., Hungary.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fernández, J., Pelegrín, B., Plastria, F. et al. Planar Location and Design of a New Facility with Inner and Outer Competition: An Interval Lexicographical-like Solution Procedure. Netw Spat Econ 7, 19–44 (2007). https://doi.org/10.1007/s11067-006-9005-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11067-006-9005-4

Keywords

Search

Navigation