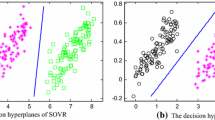
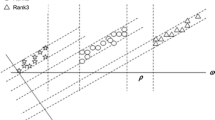
Abstract
Ordinal regression is to predict categories of ordinal scale and it has wide applications in many domains where the human evaluation plays a major role. So far several algorithms have been proposed to tackle ordinal regression problems from a machine learning perspective. However, most of these algorithms only seek one direction where the projected samples are well ranked. So a common shortcoming of these algorithms is that only one dimension in the sample space is used, which would definitely lose some useful information in its orthogonal subspaces. In this paper, we propose a novel ordinal regression strategy which consists of two stages: firstly orthogonal feature vectors are extracted and then these projector vectors are combined to learn an ordinal regression rule. Compared with previous ordinal regression methods, the proposed strategy can extract multiple features from the original data space. So the performance of ordinal regression could be improved because more information of the data is used. The experimental results on both benchmark and real datasets proves the performance of the proposed method.










Similar content being viewed by others
References
Kramer S, Widmer G, Pfahringer B, DeGroeve M (2001) Prediction of ordinal classes using regression trees. Fundamenta Informaticae 47(1–2):1–13
Herbrich R, Graepel T, Obermayer K (2000) Large margin rank boundaries for ordinal regression. In: Smola AJ, Bartlett PL, Schölkopf B, Schuurmans D (eds) Advances in large margin classifiers. MIT Press, Cambridge, pp 115–132
Crammer K, Singer Y (2002) Pranking with ranking. In: Dietterich TG, Becker S, Ghahramani Z (eds) Advances in neural information processing systems. MIT Press, Cambridge, pp 641–647
Shashua A, Levin A (2003) Ranking with large margin principle: two approaches. In: Becker S, Thrun S, Obermayer K (eds) Advances in neural information processing systems. MIT Press, Cambridge, pp 961–968
Chu W, Keerthi SS (2005) New approaches to support vector ordinal regression. In: Proceedings of the 22nd international conference on machine learning (ICML 2005). Omnipress, pp 145–152
Lin L, Lin H-T (2007) Ordinal regression by extended binary classification. In: Advances in neural information processing systems 19: proceedings of the 2006 Conference (NIPS 2006). MIT Press, pp 865–872
Cardoso JS, Pinto da Costa JF (2007) Learning to classify ordinal data: the data replication method. J Mach Learn Res 8:1393–1429
Liu Y, Liu Y, Chan KCC (2011) Ordinal regression via manifold learning. In: Proceedings of 25th AAAI conference on artificial Intelligence (AAAI11), pp 398–403
Baccianella S, Esuli A, SebastianiF F (2010) Feature selection for ordinal regression. In: Proceedings of the 2010 ACM symposium on applied computing (SAC ’10). ACM, New York, pp 1748–1754
Bishop CM (2006) Pattern recognition and machine learning. Springer, Heidelberg
Duda RO, Hart PE, Stork D (2000) Pattern classification. Wiley, Chichester
Li H, Jiang T, Zhang K (2006) Efficient and robust feature extraction by maximum margin criterion. IEEE Trans Neural Netw 17(1):157–165
Min W, Lu K, He X (2004) Locality pursuit embedding. Pattern Recognit 37(4):781–788
Zhang T, Huang K, Li X, Yang J, Tao D (2010) Generalized discriminant analysis: a matrix exponential approach. IEEE Trans Syst Man Cybern B 40(1):253–263
Xia F, Tao Q, Wang J, Zhang W (2007) Recursive feature extraction for ordinal regression. In: International joint conference on neural networks (IJCNN’07), pp 78–83
Sun B-Y, Li J, Wu DD, Zhang X-M, Li W-B (2010) Kernel discriminant learning for ordinal regression. IEEE Trans Knowl Data Eng 22(6):906–910
Ye J (2005) Characterization of a family of algorithms for generalized discriminant analysis on undersampled problems. J Mach Learn Res 6:4831502
Ji S, Ye J (2008) Generalized linear discriminant analysis: a unified framework and efficient model selection. IEEE Trans Neural Netw 19(10):1768–1782
Vapnik V (1998) The nature of statistical learning theory. Wiley, New York
Muller K-R, Mika S, Ratsch G, Tsuda K, Scholkopf B (2001) An introduction to Kernel-based learning algorithms. IEEE Trans Neural Netw 12(2):181–201
Mika S (2002) Kernel fisher discriminants. PhD thesis, University of Technology, Berlin
Guo Y, Hastie T, Tibshirani R (2007) Regularized linear discriminant analysis and its application in microarrays. Biostatistics 8(1):86–100
Kim H, Drake B, Park H (2006) Adaptive nonlinear discriminant analysis by regularized minimum squared errors. IEEE Trans Knowl Data Eng 18(5):603–612
Breiman L (1996) Bagging predictors. Mach Learn 24(2):123–140
Rosenwald A, Wright G, Chan WC, Connors JM, Campo E, Fisher RI, Gascoyne RD, Muller-Hermelink HK, Smeland EB, Staudt LM (2002) The use of molecular profiling to predict survival after chemotherapy for diffuse large-B-cell lymphoma. N Engl J Med 346(25):1937–1947
Acknowledgments
The authors sincerely thank anonymous reviewers’ constructive comments. The work of this paper has been supported by the Natural Science Foundation of China (Nos: 41101516 and 61203373), Guangdong Natural Science Foundation (No. S2011010006120) and the Shenzhen Science and Technology R & D funding Basic Research Program (No. JC201105190821A).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Sun, BY., Wang, HL., Li, WB. et al. Constructing and Combining Orthogonal Projection Vectors for Ordinal Regression. Neural Process Lett 41, 139–155 (2015). https://doi.org/10.1007/s11063-014-9340-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-014-9340-2