1 Introduction

Linear matrix equations are commonly encountered in science and engineering fields [1–5] and applied in linear least squares regression [4], disturbance decoupling [5] and linear system theorem [6, 7], etc. For example, solutions to the Sylvester matrix equation can be used to parameterize the feedback gains in pole assignment problem for linear systems [6]. Thus, many related iterative algorithms have been developed for the numerical solution of linear matrix equations [3–7]. Extending the well-known Jacobi and Gauss-Seidel iterations for system of linear equation \(Ax=b\), Ding et al. [3] derived iterative solutions of linear matrix equation as well as the generalized Sylvester matrix equation. It has been proven that the Jacobi and Gauss-Seidel algorithm completes the calculation within finite steps of iteration and has a time complexity \(O(n^3)\) [8]. Evidently, such serial-processing algorithms performed on digital computers may not be efficient enough in large-scale online applications. Especially, when applied to online solution of time-varying linear matrix equations, these related iterative algorithms should be fulfilled within every sampling period and the algorithms fail when the sampling rate is too high to allow the algorithms to complete the calculation in a single sampling period, not to mention more challenging situations.

In recent decades, as a software and hardware implementable approach [9], recurrent neural networks (RNNs) have widely arisen in scientific computation and optimization, drawing extensive interest and investigation of researchers [9–17]. Compared with traditional numerical algorithms, the neural network approach has several potential advantages in real-time applications (e.g., high-speed parallel-processing and distributed-storage natures). Therefore, RNN is generally taken into account as one of the powerful parallel-computational schemes for online solution of various challenging problems. Especially, the gradient-based RNNs designed for solving linear matrix equations are proposed and investigated [3, 7, 18]. These methods use the Frobenius norm of the error matrix as the performance criterion and design a neural network evolving along the negative gradient-descent direction to make the error norm decrease to zero with time in the time-invariant case. For the time-varying case, the Frobenius norm of the error matrix cannot converge to zero even after infinitely long time due to the lack of velocity compensation of time-varying coefficients. Quite significantly, a special class of recurrent neural network named Zhang neural network (ZNN) has been proposed to handle the lagging-error problem of the conventional gradient-based RNNs when solving time-varying problems [19–23]. Compared with gradient-based RNNs, a prominent advantage of the ZNN solution lies in that the lagging error diminishes to zero exponentially as time \(t\) goes on [19–23]. It is well known that the design of ZNN is based on a matrix- or vector-valued indefinite error function and an exponent-type formula (i.e., ZNN design formula), which makes every entry/element of the error function exponentially converge to zero. Since 2011, the concept of Zhang function has been proposed and developed from such an indefinite error function, and has been found to play the most foundational role in the development of ZNN because it largely enriches the ZNN theory [24]. By defining different Zhang functions, a series of ZNN models can be proposed for solving the same time-varying problem. Thus, it can provide various models for researchers to choose. In addition, by making good use of Zhang functions as well as the time-derivative information of the time-varying coefficients involved in time-varying problems, the resultant ZNN models can effectively avoid the lagging errors generated by gradient-based RNNs and can exponentially converge to the theoretical solution of time-varying problems.

In this paper, following the idea of Zhang function, we design two different Zhang functions for time-varying linear matrix equations. Then, based on the ZNN design formula, two ZNN models are proposed and investigated for solving such time-varying linear matrix equations. Note that such ZNN models allow us to have many choices of activation functions (e.g., any monotonically-increasing odd activation function). In addition, it has been realized that different choices of the activation function lead to different performances for RNNs (including ZNN). Therefore, this paper carries out an in-depth theoretical analysis for such two ZNN models using different activation functions. It is theoretically proved that such two ZNN models globally and exponentially converge to the theoretical solution of time-varying linear matrix equations when using linear activation functions. Inspired by the study on finite-time convergence [25, 26], we present and exploit the new activation function, which is called Li activation function [26–28], to accelerate such two ZNN models to finite-time convergence to the theoretical solution of time-varying linear matrix equations. More importantly, the upper bound of the convergence time is derived analytically via Lyapunov theory. To the best of authors’ knowledge, this is the first time to provide various ZNN models derived from different Zhang functions for solving time-varying linear matrix equations and their finite-time exact solutions to time-varying linear matrix equations.

The rest of this paper is organized into five sections. Section 2 presents the problem formulation. Section 3 designs two different Zhang functions and thus proposes two ZNN models. In Sect. 4, the convergence analysis of such two ZNN models is carried out, and the upper bound of their convergence time is derived analytically via Lyapunov theory when Li activation function is used. Section 5 substantiates the theoretical analysis of ZNN models with computer-simulation results. Section 6 concludes this paper with final remarks. Before ending this section, it is worth summarizing and listing the main contributions of this paper as follows.

  • This paper focuses on solving time-varying linear matrix equations rather than conventionally investigated static linear matrix equations, which is also quite different from Zhang et al.’s previous research on solving time-varying scalar- or vector-valued linear equations.

  • Two different Zhang functions are elaborately designed for time-varying linear matrix equations. Then, based on the ZNN design formula, two ZNN models are proposed and investigated for solving time-varying linear matrix equations.

  • The paper carries out an in-depth theoretical analysis for such two ZNN models. It is proved that such two ZNN models globally and exponentially converge to the theoretical solution of time-varying linear matrix equations when using linear activation functions. Besides, it is proved that, when using Li activation function, such two ZNN models can be further accelerated to finite-time convergence with the upper bound of the convergence time derived analytically.

  • Two illustrative examples are provided and computer-simulation results further demonstrate the effectiveness of such two ZNN models for solving time-varying linear matrix equations.

2 Problem Formulation

In this paper, let us consider the following time-varying linear matrix equation:

$$\begin{aligned} A(t)X(t)=B(t)\in R^{n\times m} , \end{aligned}$$
(1)

where \(A(t)\in R^{n\times n}\) and \(B(t)\in R^{n\times m}\) are smoothly time-varying coefficient matrices which, together with their derivatives, are assumed to be known or can be estimated accurately, and \(X(t)\in R^{n\times m}\) is an unknown matrix to be obtained. Let \(X^*(t)\in R^{n\times m}\) denote the time-varying theoretical solution of (1). This paper aims at defining different Zhang functions to generate various ZNN models for online solution of time-varying linear matrix equation (1), and then accelerating such ZNN models to finite-time convergence by finding an appropriate activation function. That is to say, an unknown \(X(t)\) can be solved by ZNN models in real time \(t\) such that it can converge to the exact time-varying theoretical solution \(X^*(t)\in R^{n\times m}\) within finite time. In order to guarantee the existence of the time-varying theoretical solution \(X^*(t)\), and also for simplicity and clarity, we limit the discussion for the situation that the given coefficient matrix \(A(t)\) is nonsingular for any time instant \(t\in [0,\infty )\).

3 Zhang Functions and ZNN Models

In this section, by defining two different Zhang functions, two ZNN models are proposed for solving time-varying linear matrix equation (1). For presentation convenience, the first ZNN model is termed ZNN-1 model, and the other one is termed ZNN-2 model.

3.1 The First Zhang Function and ZNN-1 Model

In order to solve online time-varying linear matrix equation (1), the first Zhang function (i.e., a matrix-valued lower-unbounded error function) is defined as follows:

$$\begin{aligned} E(X(t),t)=A(t)X(t)-B(t). \end{aligned}$$
(2)

Then, the ZNN design formula is adopted such that \(E(x(t),t)\) converges to zero as time \(t\) goes on; that is

$$\begin{aligned} \frac{\text{ d }{E(X(t),t)}}{\text{ d }{t}}=-\gamma \varPhi \left( E(X(t),t)\right) , \end{aligned}$$
(3)

where \(\gamma >0\in R\) denotes a positive design parameter used to scale the convergence rate of the solution, and \(\varPhi (\cdot ): R^{n\times m}\rightarrow R^{n\times m}\) denotes an activation-function matrix mapping of neural networks. It is theoretically proved that any monotonically-increasing odd activation function \(\phi (\cdot )\), being an element of matrix mapping \(\varPhi (\cdot )\), can be used for the construction of the design formula (3) [19, 20]. In the ensuing section, we are going to put research emphasis on such an activation-function matrix mapping \(\varPhi (\cdot )\), which can accelerate ZNN models’ convergence time, and even to finite-time convergence.

Now, expanding the above design formula (3) and in view of \(\dot{E}(x(t),t)=A(t)\dot{X}(t)+\dot{A}(t)X(t)-\dot{B}(t)\), we can obtain the following implicit dynamic equation of the ZNN-1 model:

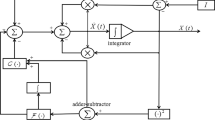
$$\begin{aligned} A(t)\dot{X}(t) =-\dot{A}(t)X(t)+\dot{B}(t)-\gamma \varPhi (A(t)X(t)-B(t)), \end{aligned}$$
(4)

where \(X(t)\in R^{n\times m}\), starting from an initial state \(X(0)\in R^{n\times m}\), denotes the state matrix corresponding to the time-varying theoretical solution \(X^*(t)\). As mentioned before, neural networks can be implemented physically by the designated hardware. In order to construct the analog circuit of ZNN-1 model (4), we can use and connect analog adders/subtractors, multipliers, integrators, and differentiators. The circuit schematic of the \(i\)th column of ZNN-1 model (4) is thus depicted in Fig. 1, which is an important and necessary step for the final hardware implementation of the neural network.

Fig. 1
figure 1

The circuit schematic which realizes the \(i\)th column of ZNN-1 model (4), where the ZNN-1 model has been rewritten as \(\dot{X}(t)=\left( I-A(t)\right) \dot{X}(t)-\dot{A}(t)X(t)+\dot{B}(t)-\gamma \varPhi \left( A(t)X(t)-B(t)\right) \) for modeling purposes

Full size image

3.2 The Second Zhang Function and ZNN-2 Model

Before defining the second Zhang function, an important theorem is presented to lay a basis for further discussion as follows.

Theorem 1

The time-derivative of time-varying matrix inversion \(A^{-1}(t)\) can be formulated as \(\dot{A}^{-1}(t)=\text{ d }A^{-1}(t)/\text{ d }t=-A^{-1}(t)\dot{A}(t)A^{-1}(t)\).

Proof

It follows from \(A(t)A^{-1}(t)=I\) that

$$\begin{aligned} \frac{\text{ d }\left( A(t)A^{-1}(t)\right) }{\text{ d }t}=\frac{\text{ d }I}{\text{ d }t}=0. \end{aligned}$$

Expanding the above equation, we obtain

$$\begin{aligned} \frac{\text{ d }A(t)}{\text{ d }t}A^{-1}(t)+A(t)\frac{\text{ d }A^{-1}(t)}{\text{ d }t}=0, \end{aligned}$$

which can be further rewritten as

$$\begin{aligned} A(t)\frac{\text{ d }A^{-1}(t)}{\text{ d }t}=-\frac{\text{ d }A(t)}{\text{ d }t}A^{-1}(t)=-\dot{A}(t)A^{-1}(t). \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{\text{ d }A^{-1}(t)}{\text{ d }t}=-A^{-1}(t)\dot{A}(t)A^{-1}(t), \end{aligned}$$

i.e.,

$$\begin{aligned} \dot{A}^{-1}(t)=-A^{-1}(t)\dot{A}(t)A^{-1}(t). \end{aligned}$$

The proof is thus complete.\(\square \)

Having the above theoretical result, we can define the second Zhang function as below:

$$\begin{aligned} E(X(t),t)=X(t)-A^{-1}(t)B(t). \end{aligned}$$
(5)

Then, in view of the above definition (5) and \(\dot{A}^{-1}(t)=-A^{-1}(t)\dot{A}(t)A^{-1}(t)\), we can obtain the ZNN-2 model by expanding ZNN design formula (3):

$$\begin{aligned} \dot{X}(t)&-[-A^{-1}(t)\dot{A}(t)A^{-1}(t)B(t)+A^{-1}(t)\dot{B}(t)]\\&=-\gamma \varPhi \left[ X(t)-A^{-1}(t)B(t)\right] , \end{aligned}$$

and equivalently

$$\begin{aligned} A(t)\dot{X}(t)&= -\dot{A}(t)A^{-1}(t)B(t)+\dot{B}(t) \nonumber \\&-\gamma A(t)\varPhi \left[ X(t)-A^{-1}(t)B(t)\right] , \end{aligned}$$
(6)

where \(X(t)\in R^{n\times m}\), starting from an initial state \(X(0)\in R^{n\times m}\), denotes the state matrix corresponding to the time-varying theoretical solution \(X^*(t)\); and the other parameters are defined as before. The reasons of proposing the ZNN-2 model are presented as follows. On one hand, ZNN-2 model (6) gives a new framework for signal processing design in a transformed space. That is to say, it can provide various models for researchers to choose. On the other hand, by using the well-known Euler forward-difference rule, a discrete-time model can be obtained from the ZNN-2 model. Then, we can exploit many existing methods (e.g., quasi-Newton BFGS method) as an alternative way of approximating the inverse of a matrix to avoid direct matrix inversion.

It is worth pointing out that, in view of the objective \(X(t)\rightarrow A^{-1}(t)B(t)\) and the use of linear activation functions, it follows from ZNN-2 model (6) that we can have

$$\begin{aligned} A(t)\dot{X}(t)=-\dot{A}(t)X(t)+\dot{B}(t)-\gamma \left( A(t)X(t)-B(t)\right) , \end{aligned}$$

which is exactly ZNN-1 model (4) using linear activation functions. Evidently, derived from different Zhang functions, the resultant ZNN models can be the same (or to say, linked). Besides, there exist clear differences by comparing such ZNN models. For example, when using nonlinear activation functions, the resultant models differ from each other. In summary, we draw a conclusion that different Zhang functions can lead to various ZNN models.

4 Convergence Analysis

In the above section, two different ZNN models are proposed to solve time-varying linear matrix equation (1). In this section, we come to prove the convergence performance of such two ZNN models using different activation functions. Specifically, the following two types of activation functions are investigated:

  1. 1)

    linear activation function

    $$\begin{aligned} \phi (e_{ij})=e_{ij}; \end{aligned}$$
    (7)
  2. 2)

    Li activation function [26–28]

    $$\begin{aligned} \phi (e_{ij})=\frac{1}{2}\text{ Lip }^r(e_{ij})+\frac{1}{2}\text{ Lip }^{1/r}(e_{ij}), \end{aligned}$$
    (8)

where \(e_{ij}\) denotes the \(ij\)th element of \(E(X(t),t)\), design parameter \(r\in (0,1)\) and the function \(\text{ Lip }^{r}(\cdot )\) is defined as

$$\begin{aligned} \text{ Lip }^{r}(e_{ij})= {\left\{ \begin{array}{ll} |e_{ij}|^r, \quad \ \ &{} \text{ if } \quad e_{ij}>0, \\ 0, \quad \ \ &{} \text{ if } \quad e_{ij}=0, \\ -|e_{ij}|^r, \quad \ \ &{} \text{ if } \quad e_{ij}<0. \\ \end{array}\right. } \end{aligned}$$

4.1 Global and Exponential Convergence

In this subsection, the global and exponential convergence results of ZNN-1 (4) and ZNN-2 (6) are presented through the following two theorems when they use linear activation function (7).

Theorem 2

Given a smoothly time-varying nonsingular coefficient matrix \(A(t)\in R^{n\times n}\) and a smoothly time-varying matrix \(B(t)\in R^{n\times m}\) in (1), if linear activation function (7) is used, then state matrix \(X(t)\in R^{n\times m}\) of ZNN-1 model (4), starting from any randomly-generated initial state \(X(0)\), converges globally exponentially to the theoretical solution of time-varying linear matrix equation (1) with time.

Proof

Let \(\tilde{X}(t)=X(t)-X^*(t)\) denote the difference between the time-varying solution \(X(t)\) generated by the proposed ZNN-1 model (4) and the time-varying theoretical solution \(X^*(t)\) of (1). Then, we have

$$\begin{aligned} X(t)=\tilde{X}(t)+X^*(t)\in R^{n\times m}. \end{aligned}$$

Substituting the above equation to (4); and in view of equation \(A(t)X^*(t)-B(t)=0\) and its time-derivative \(A(t)\dot{X}^*(t) +\dot{A}(t)X^*(t)-\dot{B}(t)=0\), we further know that \(\tilde{X}(t)\) is the solution to the ensuing dynamics:

$$\begin{aligned} A(t)\dot{\tilde{X}}(t)=-\dot{A}(t)\tilde{X}(t)-\gamma \varPhi (A(t)\tilde{X}(t)). \end{aligned}$$
(9)

On the other hand, since \(E(X(t),t)=A(t)X(t)-B(t)=A(t)[\tilde{X}(t)+X^*(t)]-B(t)=A(t)\tilde{X}(t)\), Eq. (9) can be rewritten equivalently as \(\dot{E}(X(t),t)=-\gamma \varPhi (E(X(t),t))\), which is a compact matrix form of the following set of \(n\times m\) equations

$$\begin{aligned} \dot{e}_{ij}=-\gamma \phi (e_{ij})\in R. \end{aligned}$$
(10)

Then, we can define a Lyapunov function candidate \(v=e^2_{ij}/2\geqslant 0 \) for the \(ij\)th subsystem (10). Obviously, such a Lyapunov function is positive definite, because \(v>0\) for any \(e_{ij}\ne 0\), and \(v=0\) only for \(e_{ij}=0\). Next, its time derivative can be obtained below:

$$\begin{aligned} \dot{v}=\frac{\text{ d }v}{\text{ d }t}=e_{ij}\dot{e}_{ij}=-\gamma e_{ij}\phi (e_{ij}). \end{aligned}$$

Since linear activation function \(\phi (e_{ij})=e_{ij}\) is used, we have

$$\begin{aligned} \dot{v}=-\gamma e_{ij}\phi (e_{ij})=-\gamma e^2_{ij}\leqslant 0, \end{aligned}$$

which guarantees the final negative-definiteness of \(\dot{v}\). That is to say, \(\dot{v}< 0\) for any \(e_{ij}\ne 0\), and \(\dot{v}=0\) only for \(e_{ij}= 0\). In addition, as \(e_{ij}\rightarrow \infty \), \(v\rightarrow \infty \). According to Lyapunov theory, \(e_{ij}\) globally converges to zero for any \(i\in \{1,2,\cdots ,n\},~\text{ and }~j\in \{1,2,\cdots ,m\}\). Therefore, in view of \(E(X(t),t)=A(t)\tilde{X}(t)\) and the invertible time-varying matrix \(A(t)\), we have \(\tilde{X}(t)\rightarrow 0\) as \(t\rightarrow \infty \). In other words, starting from any randomly-generated initial state \(X(0)\), state matrix \(X(t)\) of ZNN-1 model (4) converges globally to the time-varying theoretical solution \(X^*(t)\in R^{n\times m}\).

Next, we prove the exponential convergence performance of ZNN-1 model (4). In view of equation (10), we can further obtain its analytic solution in the compact matrix form (when linear activation function is used):

$$\begin{aligned} E(X(t),t)=E(X(0),0)\exp ({-\gamma t}). \end{aligned}$$

Then, we have

$$\begin{aligned} \Vert E(x(t),t)\Vert _\text{ F }=\Vert E(x(0),0)\Vert _\text{ F }\exp ({-\gamma t}), \end{aligned}$$

where \(\Vert \cdot \Vert _\text{ F }\) denotes the Frobenius norm of a matrix. Obviously, as \(t\rightarrow \infty \), \(\Vert E(x(t),t)\Vert _\text{ F }=\Vert A(t)\tilde{X}(t)\Vert _\text{ F }\rightarrow 0\) exponentially with rate \(\gamma \). Given \(\alpha >0\) as the minimum eigenvalue of \(A^\text{ T }(t)A(t)\), we have \(\Vert A(t)\tilde{X}(t)\Vert _\text{ F }=\text{ tr }\left( \tilde{X}^\text{ T }(t)A^\text{ T }(t)A(t)\tilde{X}(t)\right) \geqslant \alpha \text{ tr }\left( \tilde{X}^\text{ T }(t)\tilde{X}(t)\right) =\alpha \Vert \tilde{X}(t)\Vert _\text{ F }\) where \(\text{ tr }(\cdot )\) denotes the trace of a matrix, which implies that, starting from any randomly-generated initial state \(X(0)\), state matrix \(X(t)\) of ZNN-1 model (4) converges exponentially to time-varying theoretical solution \(X^*(t)\) of (1) as time \(t\) goes on. Based on the above analysis, the proof is thus complete. \(\square \)

Theorem 3

Given a smoothly time-varying nonsingular coefficient matrix \(A(t)\in R^{n\times n}\) and a smoothly time-varying matrix \(B(t)\in R^{n\times m}\) in (1), if linear activation function (7) is used, then state matrix \(X(t)\in R^{n\times m}\) of ZNN-2 model (6), starting from any randomly-generated initial state \(X(0)\), converges globally exponentially to the theoretical solution of time-varying linear matrix equations (1) with rate \(\gamma >0\), as time \(t\) goes on.

Proof

Let \(\tilde{X}(t)=X(t)-X^*(t)\). Substituting it to (6); and considering equation \(X^*(t)-A^{-1}(t)B(t)=0\) and its time-derivative \(\dot{X}^*(t)+A^{-1}(t)\dot{A}(t)A^{-1}(t)B(t)-A^{-1}(t)\dot{B}(t)=0\), we further know that \(\tilde{X}(t)\) is the solution to the ensuing dynamics

$$\begin{aligned} \dot{\tilde{X}}(t)=-\gamma \varPhi (\tilde{X}(t))\in R^{n\times m}. \end{aligned}$$
(11)

Thus, we can define a Lyapunov function candidate \(v=\tilde{x}^2_{ij}/2\geqslant 0 \) for the \(ij\)th subsystem of (11), where \(\tilde{x}_{ij}\) denotes the \(ij\)th element of \(\tilde{X}(t)\). Obviously, such a Lyapunov function is positive definite, because \(v>0\) for any \(\tilde{x}_{ij}\ne 0\), and \(v=0\) only for \(\tilde{x}_{ij}=0\). Then, if linear activation function (7) is used, its time derivative can be obtained below:

$$\begin{aligned} \dot{v}&=\frac{\text{ d }v}{\text{ d }t}=\tilde{x}_{ij}\dot{\tilde{x}}_{ij}=-\gamma \tilde{x}_{ij}\phi (\tilde{x}_{ij})=-\gamma \tilde{x}^2_{ij}\leqslant 0, \end{aligned}$$

which guarantees the final negative-definiteness of \(\dot{v}\). That is to say, \(\dot{v}< 0\) for any \(\tilde{x}_{ij}\ne 0\), and \(\dot{v}=0\) only for \(\tilde{x}_{ij}= 0\). In addition, as \(\tilde{x}_{ij}\rightarrow \infty \), \(v\rightarrow \infty \). By Lyapunov theory, \(\tilde{x}_{ij}\) globally converges to zero for any \(i\in \{1,2,\cdots ,n\}\) and \(j\in \{1,2,\cdots ,m\}\). Therefore, we have \(\tilde{X}(t)\rightarrow 0\) as \(t\rightarrow \infty \). That is to say, starting from any randomly-generated initial state \(X(0)\), state matrix \(X(t)\) of ZNN-2 model (6) converges globally to the time-varying theoretical solution. Now, we prove the exponential convergence of ZNN-2 model (6).

In view of Eq. (11), we can obtain its analytic solution if linear activation function (7) is used:

$$\begin{aligned} \tilde{X}(t)=\tilde{X}(0)\exp ({-\gamma t}), \end{aligned}$$

and

$$\begin{aligned} \Vert \tilde{X}(t)\Vert _\text{ F }=\Vert \tilde{X}(0)\Vert _\text{ F }\exp ({-\gamma t}), \end{aligned}$$

which means that, as \(t\rightarrow \infty \), \(\Vert \tilde{X}(t)\Vert _\text{ F }=\Vert X(t)-X^*(t)\Vert _\text{ F }\rightarrow 0\) exponentially with rate \(\gamma \). That is to say, starting from any randomly-generated initial state \(X(0)\), state matrix \(X(t)\) of ZNN-2 model (6) converges globally and exponentially to time-varying theoretical solution \(X^*(t)\) of (1) with rate \(\gamma >0\). The proof is thus complete. \(\square \)

4.2 Finite-Time Convergence

It has been realized that different choices of the activation function lead to different performances of ZNN. The convergence rate can be thoroughly improved by an elaborate design of the activation function. As proved in the above subsection, if linear activation function (7) is used, both ZNN-1 model (4) and ZNN-2 model (6) possess global and exponential convergence performance. In this subsection, we exploit Li activation function, which enables such two ZNN models to converge in finite time.

Theorem 4

Given a smoothly time-varying nonsingular coefficient matrix \(A(t)\in R^{n\times n}\) and a smoothly time-varying matrix \(B(t)\in R^{n\times m}\) in (1), if Li activation function (8) is used, then state matrix \(X(t)\) of ZNN-1 model (4), starting from any randomly-generated initial state \(X(0)\), converges to the theoretical solution of time-varying linear matrix equations (1) in finite time

$$\begin{aligned} t_c<\max \left\{ \frac{|e^-(0)|^{1-r}}{\gamma (1-r)},\frac{|e^+(0)|^{1-r}}{\gamma (1-r)}\right\} , \end{aligned}$$

where \(e^+(0)\) and \(e^-(0)\) are the largest and the smallest elements in the matrix \(A(0)X(0)-B(0)\), respectively.

Proof

For presentation convenience, we use \(E(0)=A(0)X(0)-B(0)\) standing for the initial value of Zhang function (2), i.e., \(E(X(t),t)\). Define \(e^+(t)\) to be the element in \(E(X(t),t)\) with the largest initial value \(e^+(0)=\max \{E(0)\}\); and define \(e^-(t)\) to be the element in \(E(X(t),t)\) with the smallest initial value \(e^-(0)=\min \{E(0)\}\). According to \(e^+(0)\geqslant e_{ij}(0)\) for all possible \(i\) and \(j\) and the comparison lemma [29], we know that \(e^+(t)\geqslant e_{ij}(t)\) with \(t\geqslant 0\) for all possible \(i\) and \(j\), as all dimensions in \(E(X(t),t)\) have identical dynamics \(\dot{e}_{ij}(t)=-\gamma \phi (e_{ij}(t))\) and the same Li activation function. Similarly, we get \(e^-(t)\leqslant e_{ij}(t)\) with \(t\geqslant 0\) for all possible \(i\) and \(j\). Thus, \(e^-(t)\leqslant e_{ij}(t)\leqslant e^+(t)\) for all possible \(i\) and \(j\) as time \(t\) goes on. This means that \(e_{ij}(t)\) converges to zero for all possible \(i\) and \(j\) when both \(e^+(t)\) and \(e^-(t)\) reach zero. In other words, the convergence time of ZNN-1 model (4) is bounded by the larger one between the dynamics of \(e^+(t)\) and \(e^-(t)\) , i.e., \(t_c\leqslant \max \{t_c^+,t_c^-\}\) where \(t_c^+\) and \(t_c^-\) represent the convergence time of the dynamics of \(e^+(t)\) and \(e^-(t)\), respectively.

To estimate \(t_c\), we first calculate \(t_c^+\) and \(t_c^-\). For \(t_c^+\), we have

$$\begin{aligned} \dot{e}^+(t)=-\gamma \phi (e^+(t))~\text{ with }~e^+(0)=\max \{E(0)\}, \end{aligned}$$
(12)

where \(\phi (\cdot )\) is Li activation function in this subsection. Defining a Lyapunov function candidate \(L=|e^+(t)|^2\), the time-derivative of \(L\) is thus obtained:

$$\begin{aligned} \dot{L}&= -2\gamma e^+\phi (e^+(t))\\&= -\gamma \left( |e^+(t)|^{r+1}+|e^+(t)|^{\frac{1}{r}+1}\right) \\&\leqslant -2\gamma |e^+(t)|^{r+1}\\&= -2\gamma L^{\frac{r+1}{2}}. \end{aligned}$$

Solving the above differential inequality \(\dot{L}\leqslant -2\gamma L^{\frac{r+1}{2}}\) with the initial condition \(L(0)=|e^+(0)|^2\) yields

$$\begin{aligned} L^{\frac{1-r}{2}}(t) {\left\{ \begin{array}{ll} \leqslant |e^+(0)|^{1-r}-{\gamma t(1-r)}, &{} \text{ if }~t\leqslant \frac{|e^+(0)|^{1-r}}{\gamma (1-r)}, \\ =0, &{} \text{ if }~ t>\frac{|e^+(0)|^{1-r}}{\gamma (1-r)}, \end{array}\right. } \end{aligned}$$

which means \(L(t)\) converges to zero at most after a time period \({|e^+(0)|^{1-r}}/{\gamma (1-r)}\). As a result, \(e^+(t)\) is zero for \(t>{|e^+(0)|^{1-r}}/{\gamma (1-r)}\), i.e., \(t_c^+<{|e^+(0)|^{1-r}}/{\gamma (1-r)}\). Similarly, we can conclude that \(e^-(t)\) is zero for \(t>{|e^-(0)|^{1-r}}/{\gamma (1-r)}\). That is to say, \(t_c^-<{|e^-(0)|^{1-r}}/{\gamma (1-r)}\). So we have

$$\begin{aligned} t_c<\max \left\{ \frac{|e^-(0)|^{1-r}}{\gamma (1-r)},\frac{|e^+(0)|^{1-r}}{\gamma (1-r)}\right\} , \end{aligned}$$

which means that, if Li activation function (8) is used, state matrix \(X(t)\) of ZNN-1 model (4), starting from any randomly-generated initial state \(X(0)\), converges to the theoretical solution of time-varying linear matrix equation (1) in finite time \(t_c\). This completes the proof. \(\square \)

Theorem 5

Given a smoothly time-varying nonsingular coefficient matrix \(A(t)\in R^{n\times n}\) and a smoothly time-varying matrix \(B(t)\in R^{n\times m}\) in (1), if Li activation function (8) is used, then state matrix \(X(t)\) of ZNN-2 model (6), starting from any randomly-generated initial state \(X(0)\), converges to the theoretical solution of time-varying linear matrix equation (1) in finite time

$$\begin{aligned} t_c<\max \left\{ \frac{|e^-(0)|^{1-r}}{\gamma (1-r)},\frac{|e^+(0)|^{1-r}}{\gamma (1-r)}\right\} , \end{aligned}$$

where \(e^+(0)\) and \(e^-(0)\) are the largest and the smallest elements in the matrix \(X(0)-A^{-1}(0)B(0)\), respectively.

Proof

It can be generalized from the proof of Theorem 4 by considering the initial value of Zhang function (2), and is thus omitted due to space limitation. \(\square \)

According to the theoretical analysis above, we can draw the conclusion that such two ZNN models globally and exponentially converge to the theoretical solution of time-varying linear matrix equations when using linear activation functions. If Li activation function is used, such two ZNN models can be accelerated to finite-time convergence to the theoretical time-varying solution. It is worth pointing out that the convergence time of both ZNN models can be expedited as the value of design parameter \(\gamma \) increases. For ZNN models using linear activation functions, the convergence time decreases in an exponential manner with \(\gamma \) increasing; and for ZNN models using Li activation functions, the upper bound of the convergence time has an inverse relationship with the value of design parameter \(\gamma \). That is to say, the convergence times of ZNN-1 model (4) and ZNN-2 model (6) for solving time-varying linear matrix equation (1) are decreasing as the value of \(\gamma \) increases. Therefore, design parameter \(\gamma \) plays an important role in ZNN models and thus should be selected appropriately large to satisfy the convergence rate in practice.

5 Illustrative Verification

In the previous sections, two different Zhang functions are presented, which generate two ZNN models for solving time-varying linear matrix equation (1). In addition to detailed design process of ZNN models; their excellent convergence performances are analyzed in details. In this section, two illustrative examples are provided for substantiating the efficacy of such two ZNN models. Without loss of generality, we set design parameter \(\gamma =1\) and \(r=0.1\).

Example 1

Now let us consider the following time-varying coefficients of (1) with \(A(t)\) and \(B(t)\) being respectively

$$\begin{aligned} \begin{bmatrix} \sin (3t)&\cos (3t)\\ -\cos (3t)&\sin (3t) \end{bmatrix}\text{ and } \begin{bmatrix} \sin (5t)+1&\cos (3t)\\ -\cos (3t)&\sin (5t)+2 \end{bmatrix}. \end{aligned}$$

Then, the theoretical solution \(X^*(t)\) of time-varying linear matrix equation (1) in this situation can be obtained below:

$$\begin{aligned} \begin{bmatrix} \sin (3t)&-\cos (3t)\\ \cos (3t)&\sin (3t) \end{bmatrix} \begin{bmatrix} \sin (5t)+1&\cos (3t)\\ -\cos (3t)&\sin (5t)+2 \end{bmatrix}. \end{aligned}$$

Since we have got the time-varying theoretical solution of (1), we can use it as a criterion to verify the effectiveness of such two ZNN models. The corresponding simulation results are shown in Figs. 2, 3, 4, 5 and 6.

Fig. 2
figure 2

Transient behavior of \(X(t)\) synthesized by ZNN-1 model (4) using linear activation functions starting with a randomly-generated initial state in Example 1, where red dash-dotted curves denote the time-varying theoretical solution of (1) and blue solid curves denote the neural-state solution. (Color figure online)

Full size image
Fig. 3
figure 3

Transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-1 model (4) using different activation functions in Example 1. a Using linear activation functions. b Using Li activation functions

Full size image
Fig. 4
figure 4

Transient behavior of \(X(t)\) synthesized by ZNN-2 model (6) using Li activation functions starting with a randomly-generated initial state in Example 1, where red dash-dotted curves denote the time-varying theoretical solution of (1) and blue solid curves denote the neural-state solution. (Color figure online)

Full size image
Fig. 5
figure 5

Transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-2 model (6) using different activation functions in Example 1. a Using Li activation functions. b Using linear activation functions

Full size image
Fig. 6
figure 6

Transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by different ZNN models using Li activation functions in Example 1. a By ZNN-1 model (4). b By ZNN-2 model (6)

Full size image

First, we investigate the performance of ZNN-1 model (4). If linear activation function (7) is used, starting from a randomly-generated initial state \(X(0)\in R^{2\times 2}\), the transient behavior of \(X(t)\) is shown in Fig. 2. As seen from it, state matrix \(X(t)\in R^{2\times 2}\) of ZNN-1 model (4) converges to the time-varying theoretical solution of (1) accurately. That is, \(X(t)\in R^{2\times 2}\) shown in Fig. 2 is an exact solution of time-varying linear matrix equation (1). In addition, Fig. 3a shows the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) corresponding to state matrix \(X(t)\in R^{2\times 2}\) synthesized by ZNN-1 model (4) using linear activation functions. It follows from Fig. 3a that \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) decreases exponentially to zero as time \(t\) goes on. The results demonstrate theoretical analysis of Theorem 2. Thus, the efficacy of the proposed ZNN-1 model (4) using linear activation functions for solving time-varying linear matrix equation (1) is verified primarily. On the other hand, if Li activation function (8) is used, under the same conditions, we also apply ZNN-1 model (4) to online solution of time-varying linear matrix equation (1). Figure 3b shows the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-1 model (6) using Li activation functions. It is seen from Fig. 3(b) that \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-1 model (4) decreases directly to zero within finite time \(3\) s instead of converging exponentially to zero. Compared with the results of ZNN-1 model (4) using linear activation functions, we see that ZNN-1 model (4) using Li activation functions is much superior to the one using linear activation functions, which further verifies the theoretical analysis of Theorem 4. It is worth pointing out that the transient behavior of \(X(t)\) synthesized by ZNN-1 model (4) using Li activation functions is the similar with that shown in Fig. 2 (thus not presented again).

Then, we investigate the performance of ZNN-2 model (6) under the same conditions as before. For demonstrating the effectiveness of ZNN-2 model (6) using Li activation functions, Fig. 4 shows the transient behavior of state matrix \(X(t)\in R^{2\times 2}\). As seen from it, \(X(t)\in R^{2\times 2}\) converges to the time-varying theoretical solution of (1) rapidly. Figure 5a further shows the corresponding transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\). Obviously, from Fig. 5a, we know that \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) decreases directly to zero within finite time \(3\) s. While the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\), synthesized by ZNN-2 model (6) using linear activation functions, is shown in Fig. 5b, and the corresponding transient behavior of \(X(t)\) is the similar with that shown in Fig. 4 (thus not presented again). Obviously, \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) converges exponentially to zero rather than decrease directly to zero.

For a better understanding the finite-time convergence property of ZNN models using Li activation functions, some more simulations on the convergence time of ZNN models are conducted, where 10 initial states \(X(0)\in R^{2\times 2}\) are generated randomly from \([-3,3]\in R^{2\times 2}\). Thus, the theoretical maximum of the upper bounds can be computed as follows:

$$\begin{aligned} \max \left\{ \frac{|e^-(0)|^{1-r}}{\gamma (1-r)}, \frac{|e^+(0)|^{1-r}}{\gamma (1-r)}\right\} =\frac{5^{(1-0.1)}}{1-0.1}=4.7297. \end{aligned}$$

Evidently, from the simulation results shown in Fig. 6, the convergence time of the ZNN-1 and ZNN-2 models using Li activation function is within finite time \(3\) s, which are less than the theoretically computed maximum of the upper bounds.

In summary, from the above simulation results depicted in Example 1, we can draw a conclusion that two ZNN models are both effective on solving online time-varying linear matrix equation (1). Specially speaking, if linear activation function (7) is used, such two ZNN models possess the excellent exponential-convergence performance; and if Li activation function (8) is used, two ZNN models possess the more excellent convergence performance (i.e., finite-time convergence).

Example 2

For further demonstrating the effectiveness of such two ZNN models, let us consider the following time-varying coefficients of (1):

$$\begin{aligned} A(t)= \begin{bmatrix} \cos (t)&-\sin (t)\\ \sin (t)&\cos (t) \end{bmatrix} \text{ and }~ B(t)= \begin{bmatrix} \sin (3t)&\cos (3t)&\cos (5t)\\ -\cos (3t)&\sin (3t)+2&\sin (6t) \end{bmatrix}. \end{aligned}$$

It is clear that the time-varying theoretical solution \(X^*(t)\) of (1) in this situation is

$$\begin{aligned} \begin{bmatrix} \cos (t)&\sin (t)\\ -\sin (t)&\cos (t) \end{bmatrix} \begin{bmatrix} \sin (3t)&\cos (3t)&\cos (5t)\\ -\cos (3t)&\sin (3t)+2&\sin (6t) \end{bmatrix}. \end{aligned}$$

Similarly, we apply such two ZNN models to online solution of the above time-varying linear matrix equation. First, we put emphasis on the linear activation function (7). Figure 7 show the transient behavior of state matrix \(X(t)\) synthesized by ZNN-1 model (4) using linear activation functions. As seen from Fig. 7, starting from a randomly-generated initial state \(X(0)\in R^{2\times 3}\), state matrix \(X(t)\in R^{2\times 3}\) of ZNN-1 model (4) converges to the time-varying theoretical solution of (1) in a short time. In other words, \(X(t)\in R^{2\times 3}\) is an exact solution of the above time-varying linear matrix equation. Figure 8a further shows the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) corresponding to state matrix \(X(t)\) of Fig. 7. It follows from Fig. 8a that \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-1 model (4) converges exponentially to zero as time \(t\) goes on. Along the same lines, Fig. 8b shows the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-2 model (6) using linear activation functions. The results further demonstrate the theoretical analysis of Theorems 2 and 3.

Fig. 7
figure 7

Transient behavior of \(X(t)\) synthesized by ZNN-1 model (4) using linear activation functions starting with a randomly-generated initial state in Example 2, where red dash-dotted curves denote the time-varying theoretical solution of (1) and blue solid curves denote the neural-state solution. (Color figure online)

Full size image
Fig. 8
figure 8

Transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by different ZNN models using linear activation functions in Example 2. a By ZNN-1 model (4). b By ZNN-2 model (6)

Full size image

Then, we consider Li activation function (8). Figure 9 shows the transient behavior of state matrix \(X(t)\) synthesized by ZNN-2 model (6) using Li activation functions. As seen from Fig. 9, starting from a randomly-generated initial state \(X(0)\in R^{2\times 3}\), state matrix \(X(t)\in R^{2\times 3}\) of ZNN-2 model (6) also converges to the time-varying theoretical solution of (1). Figure 10a further shows the transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) corresponding to the state matrix \(X(t)\). It is seen from Fig. 10a that \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-2 model (6) decreases directly to zero within finite time \(3\) s instead of converging exponentially to zero with time. Furthermore, as seen from Fig. 10b, \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by ZNN-1 model (4) using Li activation functions also decreases directly to zero within finite time \(3\) s. The results further demonstrate the theoretical analysis of Theorems 4 and 5. It is worth mentioning that the transient behavior of \(X(t)\) synthesized by ZNN-1 model (4) using Li activation functions is the similar with that shown in Fig. 9 and thus not presented again. Therefore, we can see that such two ZNN models are effective on solving time-varying linear matrix equation (1).

Fig. 9
figure 9

Transient behavior of \(X(t)\) synthesized by ZNN-2 model (6) using Li activation functions starting with a randomly-generated initial state in Example 2, where red dash-dotted curves denote the time-varying theoretical solution of (1) and blue solid curves denote the neural-state solution. (Color figure online)

Full size image
Fig. 10
figure 10

Transient behavior of \(\Vert A(t)X(t)-B(t)\Vert _\text{ F }\) synthesized by different ZNN models using Li activation functions in Example 2. a By ZNN-2 model (6). b By ZNN-1 model (4)

Full size image

As mentioned before, the convergence time of both ZNN models can be expedited as the value of design parameter \(\gamma \) increases. Thus, the convergence times of ZNN-1 model (4) and ZNN-2 model (6) for solving time-varying linear matrix equation (1) become shorter and shorter as the value of \(\gamma \) increases. For example, when we set \(\gamma =10^6\), the convergence time of ZNN models using Li activation functions can be expedited effectively to \(3\) microseconds. In a word, the effectiveness of the proposed ZNN models is substantiated through the theoretical analysis and computer-simulation results.

6 Conclusions

In this paper, a special class of recurrent neural network, named Zhang neural network (ZNN), has been investigated for online solution of time-varying linear matrix equations. By introducing two Zhang functions, two corresponding ZNN models are proposed to solve such time-varying linear matrix equations. Besides, two different activation functions have been investigated in ZNN models. It has been proved that such two ZNN models globally and exponentially converge to the theoretical solution of time-varying linear matrix equations when using linear activation functions. If Li activation functions have been used, such two ZNN models can be accelerated to finite-time convergence to the time-varying theoretical solution. The upper bound of the convergence time has also been derived analytically via Lyapunov theory. Computer-simulation results have further substantiated the theoretical analysis and the efficacy of ZNN models for solving time-varying linear matrix equations. Future work may lie in the circuit implementation or numerical-algorithm development of ZNN models as well as the application of ZNN models to engineering problems solving.