Abstract
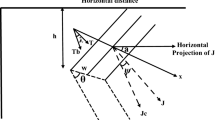
A fast and efficient technique for explanation of self-potential anomalies is of immense importance for exploration, engineering, and environmental problems. Estimation of model parameters of ore bodies in the subsurface is the primary concern in mineral exploration. In most cases, self-potential data are delineated considering various simple or idealized structures for the interpretation of lateral and vertical variations of subsurface ore bodies. In this context, we developed an inversion algorithm to determine the different parameters associated with a 2D inclined plate-type structure, which does not require any a priori information. The developed algorithm can interpret appropriately every parameter with minimum uncertainty. The position of causative source body (x0), its half-width (w) and its depth (z) were the parameters interpreted using the developed algorithm. It was found that these parameters were well resolved within the estimated uncertainty, although solutions for w showed wide variability. The technique was verified with synthetic data without noise and with different degrees of Gaussian noise. The technique was also confirmed with three field datasets for mineral exploration, and the interpreted parameters were in fair agreement with those reported in earlier works.












Similar content being viewed by others
References
Abdelazeem, M., Gobashy, M., Khalil, M. H., & Abdraboub, M. (2019). A complete model parameter optimization from self-potential data using Whale algorithm. Journal of Applied Geophysics, 170, 103825.
Abdelrahman, E. M., Abdelazeem, M., & Gobashy, M. (2019). A minimization approach to depth and shape determination of mineralized zones from potential field data using the Nelder-Mead simplex algorithm. Ore Geology Reviews, 114, 103123.
Abdelrahman, E. M., El-Araby, H. M., Hassanein, A. G., & Hafez, M. A. (2003). New methods for shape and depth determinations from SP data. Geophysics, 68, 1202–1210.
Abdelrahman, E. M., Hassaneen, A Gh, & Hafez, M. A. (1998). Interpretation of self-potential anomalies over two-dimensional plates by gradient analysis. Pure and Applied Geophysics, 152, 773–780.
Abdelrahman, E. M., & Sharafeldin, M. S. (1997). A least-squares approach to depth determination from self-potential anomalies caused by horizontal cylinders and spheres. Geophysics, 62, 44–48.
Asfahani, J., & Tlas, M. (2005). A constrained nonlinear inversion approach to quantitative interpretation of self-potential anomalies caused by cylinders, spheres and sheet-like structures. Pure and Applied Geophysics, 162, 609–624.
Biswas, A. (2013). Identification and resolution of ambiguities in interpretation of self-potential data: Analysis and integrated study around South Purulia Shear Zone, India. Ph.D. thesis, Department of Geology and Geophysics, Indian Institute of Technology Kharagpur, 199 pp. Retrieved May, 2020 from http://www.idr.iitkgp.ac.in/xmlui/handle/123456789/3247.
Biswas, A. (2016). A comparative performance of least square method and very fast simulated annealing global optimization method for interpretation of Self-Potential anomaly over 2-D inclined sheet type structure. Journal of the Geological Society of India, 88(4), 493–502.
Biswas, A. (2017). A review on modeling, inversion and interpretation of self-potential in mineral exploration and tracing Paleo-Shear zones. Ore Geology Reviews, 91, 21–56.
Biswas, A. (2018). Inversion of source parameters from magnetic anomalies for mineral/ore deposits exploration using global optimization technique and analysis of uncertainty. Natural Resources Research, 27(1), 77–107.
Biswas, A. (2019). Inversion of amplitude from the 2-D analytic signal of self-potential anomalies. In K. Essa (Ed.), Minerals (pp. 13–45). London: In-Tech Education and Publishing.
Biswas, A., & Sharma, S. P. (2014a). Resolution of multiple sheet-type structures in self-potential measurement. Journal of Earth System Science, 123(4), 809–825.
Biswas, A., & Sharma, S. P. (2014b). Optimization of Self-Potential interpretation of 2-D inclined sheet-type structures based on Very Fast Simulated Annealing and analysis of ambiguity. Journal of Applied Geophysics, 105, 235–247.
Biswas, A., & Sharma, S. P. (2015). Interpretation of self-potential anomaly over idealized body and analysis of ambiguity using very fast simulated annealing global optimization. Near Surface Geophysics, 13(2), 179–195.
Biswas, A., & Sharma, S. P. (2016). Integrated geophysical studies to elicit the structure associated with Uranium mineralization around South Purulia Shear Zone, India: A Review. Ore Geology Reviews, 72, 1307–1326.
Biswas, A., & Sharma, S. P. (2017). Interpretation of Self-potential anomaly over 2-D inclined thick sheet structures and analysis of uncertainty using very fast simulated annealing global optimization. Acta Geodaetica et Geophysica, 52(4), 439–455.
Di Maio, R., Piegari, E., Rani, P., & Avella, A. (2016a). Self-Potential data inversion through the integration of spectral analysis and tomographic approaches. Geophysical Journal International, 206, 1204–1220.
Di Maio, R., Rani, P., Piegari, E., & Milano, L. (2016b). Self-potential data inversion through a Genetic-Price algorithm. Computers & Geosciences, 94, 86–95.
Dmitriev, A. N. (2012). Forward and inverse self-potential modeling: A new approach. Russian Geology and Geophysics, 53, 611–622.
El-Kaliouby, H. M., & Al-Garani, M. A. (2009). Inversion of self-potential anomalies caused by 2D inclined sheets using neural networks. Journal of Geophysics and Engineering, 6, 29–34.
Eppelbaum, L., & Khesin, B. (2012). Methodological specificities of geophysical studies in the complex environments of the caucasus. In L. Eppelbaum & B. Khesin (Eds.), Geophysical studies in the caucasus (pp. 39–138). Berlin: Springer.
Essa, K. S. (2011). A new algorithm for gravity or self-potential data interpretation. Journal of Geophysics and Engineering, 8, 434–446.
Essa, K. S., & El-Hussein, M. (2017). A new approach for the interpretation of self-potential data by 2-D inclined plate. Journal of Applied Geophysics, 136, 455–461.
Essa, K., Mahanee, S., & Smith, P. D. (2008). A new inversion algorithm for estimating the best fitting parameters of some geometrically simple body to measured self-potential anomalies. Exploration Geophysics, 39, 155–163.
Gobashy, M., Abdelazeem, M., Abdrabou, M., & Khalil, M. H. (2020). Estimating model parameters from self-potential anomaly of 2D inclined sheet using whale optimization algorithm: Applications to mineral exploration and tracing shear zones. Natural Resources Research, 29, 499–519.
Göktürkler, G., & Balkaya, Ç. (2012). Inversion of self-potential anomalies caused by simple geometry bodies using global optimization algorithms. Journal of Geophysics and Engineering, 9, 498–507.
Hafez, M. A. (2005). Interpretation of the self-potential anomaly over a 2D inclined plate using a moving average window curves method. Journal of Geophysics and Engineering, 2, 97–102.
Ingber, L., & Rosen, B. (1992). Genetic algorithms and very fast simulated reannealing: A comparison. Mathematical and Computer Modeling, 16(11), 87–100.
Jagannadha, R. S., Rama, R. P., & Radhakrishna, M. I. V. (1993). Automatic inversion of self-potential anomalies of sheet-like bodies. Computers & Geosciences, 19, 61–73.
Jardani, A., Revil, A., Boleve, A., & Dupont, J. P. (2008). Three-dimensional inversion of self-potential data used to constrain the pattern of groundwater flow in geothermal fields. Journal of Geophysical Research-Solid Earth, 113, B09204.
Kaikkonen, P., & Sharma, S. P. (1998). 2-D nonlinear joint inversion of VLF and VLF-R data using simulated annealing. Journal of Applied Geophysics, 39, 155–176.
Kulessa, B., Hubbard, B., & Brown, G. H. (2003). Cross-coupled flow modeling of coincident streaming and electrochemical potentials and application to sub-glacial self-potential data. Journal of Geophysical Research, 108(B8), 2381.
Lile, O. B. (1994). Modeling self-potential anomalies from electric conductors. In EAGE 56th meeting and technical exhibition (Vienna, Austria).
Mehanee, S. (2014). An efficient regularized inversion approach for self-potential data interpretation of ore exploration using a mix of logarithmic and non-logarithmic model parameters. Ore Geology Reviews, 57, 87–115.
Mehanee, S. (2015). Tracing of paleo-shear zones by self-potential data inversion: case studies from the KTB, Rittsteig, & Grossensees graphite-bearing fault planes. Earth, Planets and Space, 67, 14–47.
Mehanee, S., Essa, K. S., & Smith, P. D. (2011). A rapid technique for estimating the depth and width of a two-dimensional plate from self-potential data. Journal of Geophysics and Engineering, 8, 447–456.
Mendonca, C. A. (2008). Forward and inverse self-potential modeling in mineral exploration. Geophysics, 73, F33–F43.
Monteiro Santos, F. A. (2010). Inversion of self-potential of idealized bodies anomalies using particle swarm optimization. Computers & Geosciences, 36, 1185–1190.
Mosegaard, K., & Tarantola, A. (1995). Monte Carlo sampling of solutions to inverse problems. Journal of Geophysical Research, 100(B7), 12431–12447.
Murthy, B. V. S., & Haricharan, P. (1984). Self-potential anomaly over double line of poles—interpretation through log curves. Proceedings Indian Academy of Science (Earth and Planetary Science), 93, 437–445.
Murthy, B. V. S., & Haricharan, P. (1985). Nomograms for the complete interpretation of spontaneous potential profiles over sheet like and cylindrical 2D structures. Geophysics, 50, 1127–1135.
Murthy, I. V. R., Sudhakar, K. S., & Rao, P. R. (2005). A new method of interpreting self- potential anomalies of two-dimensional inclined sheets. Computers & Geosciences, 31, 661–665.
Paul, M. K. (1965). Direct interpretation of self-potential anomalies caused by inclined sheets of infinite extension. Geophysics, 30, 418–423.
Paul, M. K., Data, S., & Banerjee, B. (1965). Interpretation of SP anomalies due to localized causative bodies. Pure and Applied Geophysics, 61, 95–100.
Rao, A. D., Babu, H., & SivakumarSinha, G. D. (1982). A Fourier transform method for the interpretation of self-potential anomalies due to two-dimensional inclined sheet of finite depth extent. Pure and Applied Geophysics, 120, 365–374.
Rao, B. S. R., Murthy, I. V. R., & Reddy, S. J. (1970). Interpretation of self-potential anomalies of some simple geometrical bodies. Pure and Applied Geophysics, 78, 60–77.
Rothman, D. H. (1985). Nonlinear inversion, statistical mechanics and residual statics estimation. Geophysics, 50, 2784–2796.
Rothman, D. H. (1986). Automatic estimation of large residual statics correction. Geophysics, 51, 337–346.
Roudsari, M. S., & Beitollahi, A. (2013). Forward modeling and inversion of self-potential anomalies caused by 2D inclined sheets. Exploration Geophysics, 44, 176–184.
Roudsari, M. S., & Beitollahi, A. (2015). Laboratory modelling of self-potential anomalies due to spherical bodies. Exploration Geophysics, 46, 320–331.
Roy, S. V. S., & Mohan, N. L. (1984). Spectral interpretation of self-potential anomalies of some simple geometric bodies. Pure and Applied Geophysics, 78, 66–77.
Sato, M., & Mooney, H. M. (1960). The electrochemical mechanism of sulfide self-potentials. Geophysics, 25, 226–249.
Sen, M. K., & Stoffa, P. L. (1996). Bayesian inference, Gibbs sampler and uncertainty estimation in geophysical inversion. Geophysical Prospecting, 44, 313–350.
Sen, M. K., & Stoffa, P. L. (2013). Global optimization methods in geophysical inversion (2nd ed.). London: Cambridge Publisher.
Sharma, S. P. (2012). VFSARES—A very fast simulated annealing FORTRAN program for interpretation of 1-D DC resistivity sounding data from various electrode array. Computers & Geosciences, 42, 177–188.
Sharma, S. P., & Biswas, A. (2013). Interpretation of self-potential anomaly over 2D inclined structure using very fast simulated annealing global optimization–An insight about ambiguity. Geophysics, 78(3), WB3–WB15.
Sundararajan, N., Arun Kumar, I., Mohan, N. L., & SeshagiriRao, S. V. (1990). Use of Hilbert transform to interpret self-potential anomalies due to two dimensional inclined sheets. Pure Applied Geophysics, 133, 117–126.
Sundararajan, N., Srinivasa Rao, P., & Sunitha, V. (1998). An analytical method to interpret self-potential anomalies caused by 2D inclined sheets. Geophysics, 63, 1551–1555.
Tlas, M., & Asfahani, J. (2007). A best-estimate approach for determining self-potential parameters related to simple geometric shaped structures. Pure and Applied Geophysics, 164, 2313–2328.
Tlas, M., & Asfahani, J. (2013). An approach for interpretation of self-potential anomalies due to simple geometrical structures using flair function minimization. Pure and Applied Geophysics, 170, 895–905.
Trivedi, S., Kumar, P., Parija, M. P., & Biswas, A. (2020). Global optimization of model parameters from the 2-D analytic signal of gravity and magnetic anomalies. In A. Biswas & S. P. Sharma (Eds.), Advances in modeling and interpretation in near surface geophysics (pp. 189–221). Berlin: Springer.
Acknowledgments
We would like to thank the Editor-in-Chief Prof. John Carranza and two anonymous reviewers for their comments, which have helped to improve the work. This work forms a part of the Ph.D. thesis of KR, who thank the Council of Scientific and Industrial Research (CSIR), New Delhi, for the research fellowship. This work is a result of a modeling approach in connection with the prospective proposal on the interpretation of mineral exploration study for submission to the Institute of Eminence (IoE) research grant, BHU by AB.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rao, K., Jain, S. & Biswas, A. Global Optimization for Delineation of Self-potential Anomaly of a 2D Inclined Plate. Nat Resour Res 30, 175–189 (2021). https://doi.org/10.1007/s11053-020-09713-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11053-020-09713-4