Skip to main content
SpringerLink
Log in

A short note for numerical analysis of dynamic contact considering impact and a very stiff spring-damper constraint on the contact point

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

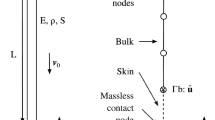
By extending the numerical technique suggested by the author for the dynamic contact problem having a very stiff spring on the contact point, it is shown that the dynamic contact problem having a very stiff damper as well as a spring on the contact point can be time integrated without instability by imposing the time-differentiated constraints with the unconditionally stable Newmark time integration rule. It is also shown that the dynamic contact involving the repeated impacts and separations can be solved without instability by using the same time-differentiated constraints, and that the spring-damper deformation (i.e., penetration) on the contact point at the time of impact (i.e., at the first time step of contact) can be most reasonably determined by the displacement contact constraint. The special features of the present technique to solve the impact problem having a very stiff spring-damper on the contact point are that the equation of motion may be time integrated with any convenient ODE technique, and that the time step size reduction or the penetration threshold need not be considered at the time of impact.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Flores, P., Ambrosio, J., Claro, J.C.P., Lankarani, H.M.: Influence of the contact-impact force model on the dynamic response of multi-body systems. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 220, 21–34 (2006)

    Google Scholar 

  2. Flores, P., Ambrosio, J., Claro, J.C.P., Lankarani, H.M.: Dynamic behavior of planar rigid multi-body systems including revolute joints with clearance. Proc. Inst. Mech. Eng., Part K, J. Multi-Body Dyn. 221, 161–174 (2007)

    Google Scholar 

  3. Ambrosio, J., Verissimo, P.: Improved bushing models for general multibody systems and vehicle dynamics. Multibody Syst. Dyn. 22, 341–365 (2009)

    Article  MATH  Google Scholar 

  4. Shabana, A.A., Zaazaa, K.E., Escalona, J.L., Sany, J.R.: Development of elastic force model for wheel/rail contact problems. J. Sound Vib. 269, 295–325 (2004)

    Article  Google Scholar 

  5. Tian, Q., Zhang, Y., Chen, L., Flores, P.: Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints. Comput. Struct. 87, 913–929 (2009)

    Article  Google Scholar 

  6. Flores, P., Ambrosio, J.: On the contact detection for contact-impact analysis in multibody systems. Multibody Syst. Dyn. 24, 103–122 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Crowther, A.R., Singh, R., Zhang, N., Chapman, C.: Impulsive response of an automatic transmission system with multiple clearances: Formulation, simulation and experiment. J. Sound Vib. 306, 444–466 (2007)

    Article  Google Scholar 

  8. Chan, C., Pisano, A.P.: Dynamic model of a fluctuating rocker-arm ratio cam system. Trans. ASME J. Mech. Trans. Autom. Des. 109, 356–365 (1987)

    Article  Google Scholar 

  9. Djerassi, S.: Collision with friction; Part A: Newton’s hypothesis. Multibody Syst. Dyn. 21, 37–54 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Djerassi, S.: Collision with friction; Part B: Poisson’s and Stronge’s hypothesis. Multibody Syst. Dyn. 21, 55–70 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  11. Flores, P., Leine, R., Glocker, C.: Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody Syst. Dyn. 23, 165–190 (2010)

    Article  MathSciNet  Google Scholar 

  12. Lee, K.: A stabilized numerical solution for dynamic contact of bodies having very stiff constraint on the contact point. Comput. Mech. 46, 533–543 (2010)

    Article  MATH  Google Scholar 

  13. Vu-Quoc, L., Olsson, M.: Formulation of a basic building block model for interaction of high speed vehicles on flexible structures. J. Appl. Mech. 56, 451–458 (1989)

    Article  MATH  Google Scholar 

  14. Lee, K.: Numerical analysis for dynamic contact between high-speed wheel and elastic beam with Coulomb friction. Int. J. Numer. Methods Eng. 78, 883–900 (2009)

    Article  MATH  Google Scholar 

  15. Lee, K.: Analysis of dynamic contact between rotating spur gears by finite element and multi-body dynamics techniques. Proc. Inst. Mech. Eng., Part C, J. Mech. Eng. Sci. 215, 423–435 (2001)

    Article  Google Scholar 

  16. Lee, K.: A numerical method for dynamic analysis of vehicles moving on flexible structures having gaps. Int. J. Numer. Methods Eng. 40, 511–531 (1997)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Chonbuk National University, Jeonju, Jeonbuk, 561-756, Korea

    Kisu Lee

Authors
  1. Kisu Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kisu Lee.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lee, K. A short note for numerical analysis of dynamic contact considering impact and a very stiff spring-damper constraint on the contact point. Multibody Syst Dyn 26, 425–439 (2011). https://doi.org/10.1007/s11044-011-9257-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-011-9257-8

Keywords

Search

Navigation