Abstract
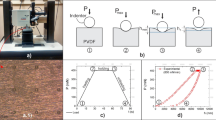
In this study, we investigate the indentation of viscoelastic composites. The composite is assumed to consist of two phases, i.e., the filler and the matrix, which are linear elastic and linear viscoelastic material, respectively. Two cases are investigated: (1) hard fillers are scattered in a very soft matrix; (2) the matrix is much harder than the fillers. Particular attention is paid to the correlation between the indentation relaxation loads and the material and geometric parameters of the composite system. To this end, we perform a theoretical analysis which is followed by finite element analysis. Our main result is a simple relation correlating the reduced relaxation modulus of the matrix, E m,r (t), with the indentation relaxation load P(t), i.e., E m,r (t)=P(t)/P(0), where P(0) represents the indentation load at the starting point of the relaxation test. This result on one hand indicates that for the two cases under study the relaxation feature of the indentation load is determined by the reduced relaxation modulus of the matrix. On the other hand, the result shows that the reduced relaxation modulus of the matrix of the composites may be simply determined from the indentation relaxation load without invoking the knowledge of both the indenter geometry and the profile of indented solids.
Similar content being viewed by others
References
ABAQUS User’s Manual, version 6.8: Providence: Hibbit, Karlsson & Sorenson (2008)
Barenblatt, G.I.: Scaling, Self-similarity and Intermediate Asymptotics. Cambridge University Press, Cambridge (1996)
Cao, Y.P.: Determination of the creep exponent of a power-law creep solid using indentation tests. Mech. Time-Depend. Mater. 11, 159–172 (2007)
Cao, Y.P., Ma, D.C., Raabe, D.: The use of flat punch indentation to determine the viscoelastic properties in the time and frequency domains of a soft layer bonded to a rigid substrate. Acta Biomaterialia 5, 240–248 (2009)
Cao, Y.P., Ji, X.Y., Feng, X.Q.: Geometry independence of the normalized relaxation functions of viscoelastic materials in indentation. Philos. Mag. 90, 1639–1655 (2010)
Cheng, Y.T., Cheng, C. M.: Scaling, dimensional analysis, and indentation measurements. Mater. Sci. Eng., R Rep. 44, 91–149 (2004)
Cheng, Y.T., Yang, F.Q.: Obtaining shear relaxation modulus and creep compliance of linear viscoelastic materials from instrumented indentation using axisymmetric indenters of power-law profiles. J. Mater. Res. 24, 3013–3017 (2009)
Cheng, Y.T., Ni, W.Y., Cheng, C.M.: Nonlinear analysis of oscillatory indentation in elastic and viscoelastic solids. Phys. Rev. Lett. 97, 075506 (2006)
Christensen, R.M.: Theory of Viscoelasticity: An Introduction. Academic Press, San Diego (1982)
Ebenstein, D.M., Pruitt, L.A.: Nanoindentation of biological materials. Nano Today 1, 26 (2006)
Fischer-Cripps, A.C.: Multiple-frequency dynamic nanoindentation testing. J. Mater. Res. 19, 2981–2989 (2004)
Fung, Y.C.: Biomechanics: Mechanical Properties of Living Tissues. Springer, New York (1993)
Giannakopoulos, A.E.: Elastic and viscoelastic indentation of flat surfaces by pyramid indentors. J. Mech. Phys. Solids 54, 1305–1332 (2006)
Graham, G.A.C.: The contact problem in the linear theory of viscoelasticity. Int. J. Eng. Sci. 3, 27–45 (1965)
Herbert, E.G., Oliver, W.C., Lumsdaine, A., Pharr, G.M.: Measuring the constitutive behavior of viscoelastic solids in the time and frequency domain using flat punch nanoindentation. J. Mater. Res. 24, 626–637 (2009)
Huang, G., Lu, H.B.: Measurement of Young’s relaxation modulus using nanoindentation. Mech. Time-Depend. Mater. 10, 229–243 (2006)
Levental, I., Georges, P.C., Janmey, P.A.: Soft biological materials and their impact on cell function. Soft Matter 3, 299–206 (2007)
Lee, B., Han, L., Frank, E.H., Chubinskaya, S., Ortiz, C., Grodzinsky, A.J.: Dynamic mechanical properties of the tissue-engineered matrix associated with individual chondrocytes. J. Biomech. 43, 469–476 (2010)
Liu, Y.J., Nishimura, N., Otani, Y.: Large-scale modeling of carbon-nanotube composites by a fast multipole boundary element method. Comput. Mater. Sci. 34, 173–187 (2005)
Lu, H., Wang, B., Ma, J., Huang, G., Viswanathan, H.: Measurement of creep compliance of solid polymers by nanoindentation. Mech. Time-Depend. Mater. 7, 189–207 (2003)
Ngan, A.H.W., Wang, H.T., Tang, B., Sze, K.Y.: Correcting power-law viscoelastic effects in elastic modulus measurement using depth-sensing indentation. Int. J. Solids Struct. 42, 1831–1846 (2005)
Oyen, M.L.: Spherical indentation creep following ramp loading. J. Mater. Res. 20, 2094–2100 (2005)
Oyen, M.L.: Sensitivity of polymer nanoindentation creep measurements to experimental variables. Acta Mater. 55, 3633 (2007)
Oyen, M.L., Cook, R.F.J.: Load–displacement behavior during sharp indentation of viscous–elastic–plastic materials. J. Mater. Res. 18, 139 (2003)
Ramakrishna, S., Huang, Z.M., Kumar, G.V., Batchelor, A.W., Mayer, J.: An Introduction to Biocomposites. Imperial College Press, London (2004)
Shimizu, S., Yanagimoto, T., Sakai, M.: Pyramidal indentation load-depth curve of viscoelastic materials. J. Mater. Res. 14, 4075–4086 (1999)
Thomas, V., Dean, D.R., Jose, M.V., Mathew, B., Chowdhury, S., Vohra, Y.K.: Nanostructured biocomposite scaffolds based on collagen coelectrospun with nanohydroxyapatite. Biomacromolecules 8, 631–637 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cao, YP., Chen, KL. Theoretical and computational modelling of instrumented indentation of viscoelastic composites. Mech Time-Depend Mater 16, 1–18 (2012). https://doi.org/10.1007/s11043-011-9132-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11043-011-9132-2