Skip to main content
SpringerLink
Log in

Construction of a new 2D Chebyshev-Sine map and its application to color image encryption

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

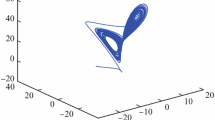
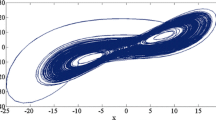
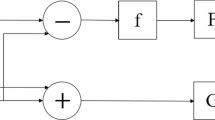
A new 2D Chebyshev-Sine map with natural evaluation is proposed and its dynamical behavior is analyzed. To investigate its application in information security, a color image encryption algorithm is designed. One-time initial condition expressed as ordered quaternion is extracted from colored non Gaussian noise before each encryption process. The algorithm can achieve desired effect after two rounds by exclusive or (XOR) operation with avalanche effect. Simulation results demonstrated that the speed is fast, so the algorithm is suitable for image encryption over the Cloud.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Abdallah E, Ben AH, Prabir B (2007) MPEG video watermarking using tensor singular value decomposition. //International Conference Image Analysis and Recognition. Springer, Berlin, Heidelberg

  2. Akhshani A, Akhavan A, Mobaraki A et al (2014) Pseudo random number generator based on quantum chaotic map[J]. Commun Nonlinear Sci Numer Simul 19(1):101–111

    Article  MATH  Google Scholar 

  3. Arroyo D, Rhouma R, Alvarez G et al (2008) On the security of a new image encryption scheme based on chaotic map lattices[J]. Chaos 18(3):033112

    Article  Google Scholar 

  4. Banerjee S, Yorke JA, Grebogi C (1998) Robust chaos[J]. Phys Rev Lett 80(14):3049

    Article  MATH  Google Scholar 

  5. Belazi A, Khan M, El-Latif AAA et al (2017) Efficient cryptosystem approaches: S-boxes and permutation–substitution-based encryption[J]. Nonlinear Dyn 87(1):337–361

    Article  Google Scholar 

  6. Cong L, Wu X, Sun S (1999) A general efficient method for chaotic signal estimation[J]. IEEE Trans Signal Process 47(5):1424–1428

    Article  Google Scholar 

  7. Gao Z, Chen D, Zhang W et al (2017) Colour image encryption algorithm using one-time key and FrFT[J]. IET Image Process 12(4):472–478

    Article  Google Scholar 

  8. Hamza AB, Krim H (2003) Jensen-Rényi divergence measure: theoretical and computational perspectives[C]//Information Theory, 2003. Proceedings. IEEE International Symposium on. IEEE, p 257–257

  9. Hussain I, Shah T, Gondal MA (2012) Image encryption algorithm based on PGL(2,GF(28)) S-boxes and TD-ERCS chaotic sequence. Nonlinear Dyn 70(1):181–187

    Article  Google Scholar 

  10. Kadir A, Aili M, Sattar M (2017) Color image encryption scheme using coupled hyper chaotic system with multiple impulse injections. Optik 129:231–238

    Article  Google Scholar 

  11. Kurian AP, Leung H (2009) Weak signal estimation in chaotic clutter using model-based coupled synchronization[J]. IEEE Trans Circuits Syst I 56(4):820–828

    Article  MathSciNet  Google Scholar 

  12. L'Ecuyer P, Simard R (2013) TestU01: a software library in ANSI C for empirical testing of random number generators--user’s guide, Compact Version[J]

  13. Liu H, Kadir A, Sun X (2017) Chaos-based fast colour image encryption scheme with true random number keys from environmental noise[J]. IET Image Process 11(5):324–332

    Article  Google Scholar 

  14. Luo C, Wang X (2014) Adaptive modified function projective lag synchronization of hyperchaotic complex systems with fully uncertain parameters[J]. J Vib Control 20(12):1831–1845

    Article  MathSciNet  MATH  Google Scholar 

  15. Rozenbaum EB, Ganeshan S, Galitski V (2017) Lyapunov exponent and out-of-time-ordered correlator’s growth rate in a chaotic system[J]. Phys Rev Lett 118(8):086801

    Article  Google Scholar 

  16. Seyedzadeh SM, Mirzakuchaki S (2012) A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal Process 92(5):1202–1215

    Article  Google Scholar 

  17. Shanon CE (1949) Communication theory of secrecy systems. Bell Syst Tech J 28(4):656–715

    Article  MathSciNet  Google Scholar 

  18. Wang X, Guo K (2014) A new image alternate encryption algorithm based on chaotic map[J]. Nonlinear Dyn 76(4):1943–1950

    Article  MATH  Google Scholar 

  19. Wang XY, Zhang YQ, Zhao YY (2015) A novel image encryption scheme based on 2-D logistic map and DNA sequence operations[J]. Nonlinear Dyn 82(3):1269–1280

    Article  MathSciNet  Google Scholar 

  20. Wang X, Wang S, Zhang Y et al (2018) A one-time pad color image cryptosystem based on SHA-3 and multiple chaotic systems[J]. Opt Lasers Eng 103:1–8

    Article  Google Scholar 

  21. Wang C, Wang X, Xia Z, Zhang C (2019) Ternary radial harmonic Fourier moments based robust stereo image zero-watermarking algorithm. Inf Sci 470:109–120

    Article  Google Scholar 

  22. Xiao D, Zhang YS (2014) Self-adaptive permutation and combined global diffusion for chaotic color image encryption. AEU Int J Electron Commun 68(4):361–368

    Article  Google Scholar 

  23. Ye G, Huang X (2017) An efficient symmetric image encryption algorithm based on an intertwining logistic map[J]. Neurocomputing 251:45–53

    Article  Google Scholar 

  24. Ye G, Zhao H, Chai H (2016) Chaotic image encryption algorithm using wave-line permutation and block diffusion[J]. Nonlinear Dyn 83(4):2067–2077

    Article  MathSciNet  Google Scholar 

  25. Zhang Y, Xiao D (2014) An image encryption scheme based on rotation matrix bit-level permutation and block diffusion[J]. Commun Nonlinear Sci Numer Simul 19(1):74–82

    Article  MATH  Google Scholar 

  26. Zhen P, Zhao G, Min L, Jin X (2016) Chaos-based image encryption scheme combining DNA coding and entropy. Multimed Tools Appl 75(11):6303–6319

    Article  Google Scholar 

Download references

Acknowledgments

This research is supported by the National Natural Science Foundation of China (No: 61662073, 61363082), the Natural Science Foundation of Shandong Province (No: ZR2018LF006).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Jinan, Jinan, 250022, Shandong, China

    Hongjun Liu & Fengtong Wen

  2. Shandong Famous Teacher’s Workshop, Weifang Vocational College, Weifang, 261041, Shandong, China

    Hongjun Liu

  3. School of Computer Science and Engineering, Xinjiang University of Finance and Economics, Urumqi, 830012, China

    Abdurahman Kadir

Authors
  1. Hongjun Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fengtong Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abdurahman Kadir
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongjun Liu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest concerning the publication of this manuscript.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, H., Wen, F. & Kadir, A. Construction of a new 2D Chebyshev-Sine map and its application to color image encryption. Multimed Tools Appl 78, 15997–16010 (2019). https://doi.org/10.1007/s11042-018-6996-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-018-6996-z

Keywords

Search

Navigation