Fracture of a composite reinforced by unidirectional fibers

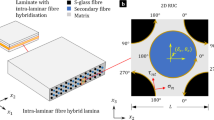
An elastic medium weakened by a periodic system of circular holes filled with homogeneous elastic fibers whose surface is coated with a homogeneous film is considered. A fracture model for a medium with a periodic structure is proposed, which is based on an analysis of the fracture zone near the crack tip. It is assumed that the fracture zone is a layer of finite length containing a material with partially broken bonds between separate structural elements (end zone). The fracture zone is considered as part of the crack. The bonds between crack faces in the end zone are modeled by applying the cohesive forces caused by the presence of bonds to the crack surface. An analysis of the limit equilibrium of shear cracks in the end zone of the model is performed on the basis of a nonlocal fracture criterion together with a force condition for the motion of crack tip and a deformation condition for determining the motion of faces of end-zone cracks. In the analysis, relationships between the cohesive forces and the shear of crack faces are established, the stress state near the crack is assessed with account of external loading, cohesive forces, and fiber arrangement, and the critical external loads as functions of geometric parameters of the composite are determined.