Skip to main content
SpringerLink
Log in

Superposition of large butt-end and coaxial torsional and axial shear deformations of homogeneous and fiber-reinforced thick-wall cylinders

  • Published:
Mechanics of Composite Materials Aims and scope

Abstract

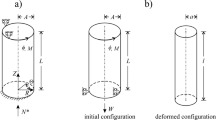
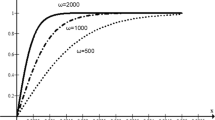
A mathematical model of superposition of large butt-end and coaxial torsional and axial shear deformations of homogeneous and fiber-reinforced thick-wall cylinders is constructed. The macroscopic stresses of the reinforced material are additively determined by matrix stresses and by tensile or constrained compression stresses in the reinforcing fibers. The model is based on the numerical solution of two boundary-value problems, one of which corresponds to the butt-end torsion and the other to the coaxial torsion and axial shear. The boundary-value problem on joint deformations is solved with the use of the displacement field determined from the solution to the boundary-value problem on butt-end torsion. The results obtained by applying this method to homogeneous and axially-radially reinforced thick-wall cylinders subjected to butt-end torsion with subsequent coaxial torsion and axial shear are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. E. Green and J. E. Adkins, Large Elastic Deformations and Non-Linear Continuum Mechanics, Clarendon Press, Oxford (1960).

    Google Scholar 

  2. A. I. Lur’e, Nonlinear Elasticity Theory [in Russian], Nauka, Moscow (1980).

    Google Scholar 

  3. K. F. Chernykh, “Biomechanics of soft tissue (in the eyes of a strength expert),” in: Trans. I All-Union Symp. “Nonlinear Theory of Thin-Walled Structures and Biomechanics,” [in Russian], Kutaisi-Tkibuli, 22–24 May (1985), pp. 469–481.

  4. V. G. Ryzhankov and K. F. Chernykh, “Nonlinear deformation of a thick-walled cylinder,” in: Applied Problems of Strength and Plasticity: Algorithmization and Automation of Scientific Investigations [in Russian], Gorki (1988), pp. 98–104.

  5. K. F. Chernykh, Introduction to the Anisotropic Elasticity [in Russian], Nauka, Moscow (1988).

    Google Scholar 

  6. V. M. Akhundov, “Large tensile, inflation, and torsional deformations of a round cylinder,” Probl. Obchisl. Mekh. Mitsn. Konstr., Dnipr. Nats. Univ., Dnipropetrovs’k, Iss. 8., 9–20 (2004).

  7. V. M. Akhundov, “Applied model of a round cylinder reinforced with systems of yarns at large tensile, inflation, and torsional deformations,” Mech. Compos. Mater., 43, No. 2, 159–172 (2007).

    Article  Google Scholar 

  8. V. M. Akhundov, “Applied theory of composites with small contents of yarns under large deformations,” Mekh. Kompozits. Mater. Konstr., 7, No. 1, 3–15 (2001).

    Google Scholar 

  9. K. F. Chernykh (ed.), Introduction to the Continuum Mechanics [in Russian], Izdat. Leningrad. Univ., Leningrad (1984).

    Google Scholar 

  10. V. M. Akhundov, “Method of calculation of deformational characteristics of composites with small contents of yarns under large deformations,” Visn. Dnipropetr. Univ. Ser. Mekhanika, Iss. 5, 1, 151–160 (2001).

    Google Scholar 

  11. V. M. Akhundov, “Analysis of elastomeric composites based on fiber-reinforced systems. 1. Development of design methods for composite materials,” Mech. Compos. Mater., 34, No. 6, 515–524 (1998).

    Article  Google Scholar 

  12. G. A. Kom and T. M. Kom, Mathematical Handbook for Scientists and Engineers, McGraw-Hill Book Company, New York-San Francisco-Toronto-London-Sydney (1968).

    Google Scholar 

  13. J. Ortega and V. Reinboldt, Iterative Methods of Solving Nonlinear Equation Systems with Many Unknowns [Russian translation], Mir, Moscow (1975).

    Google Scholar 

  14. M. Levinson and I. W. Burgess, “A comparison of some simple constitutive relations for slightly compressible rubber-like materials,” Int. J. Mech. Sci., 13, 563–572 (1971).

    Article  Google Scholar 

  15. P. J. Blatz and W. L. Ko, “Application of finite elastic theory to the deformation of rubber materials,” Trans. Soc. Rheol, 7, No. 6, 223–251 (1962).

    Article  Google Scholar 

  16. R. V. Uzina, I. P. Nagdaseva, V. A. Pugin, and B. I. Volnukhin, Processing Technology of Tire Cord [in Russian], Khimiya, Moscow (1986).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Metallurgical Academy of Ukraine, Dnepropetrovsk, Ukraine

    V. M. Akhundov & T. A. Skripochka

Authors
  1. V. M. Akhundov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. A. Skripochka
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Translated from Mekhanika Kompozitnykh Materialov, Vol. 43, No. 4, pp. 465–492, July–August, 2007.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Akhundov, V.M., Skripochka, T.A. Superposition of large butt-end and coaxial torsional and axial shear deformations of homogeneous and fiber-reinforced thick-wall cylinders. Mech Compos Mater 43, 311–330 (2007). https://doi.org/10.1007/s11029-007-0030-2

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-007-0030-2

Keywords

Search

Navigation