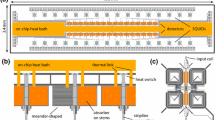
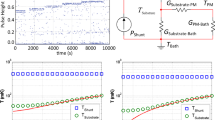
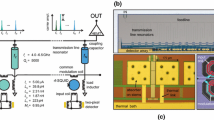
The design of a magnetic calorimeter for the measurement of releases of energy that correspond to a number of rare events, for example, cosmic particles, particles of dark matter, isolated x-ray quanta, and so on, is proposed. The calorimeter is set into a working state by means of the method of adiabatic demagnetization and the response to energy release is measured by a quantum interferometer (squid). The action of the calorimeter in different practical problems is considered, and the sensitivity of the device and its measurement precision are estimated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. Barone and J. Paterno, The Josephson Effect. Physics and Applications [Russian translation], Mir, Moscow (1984).
J. Clarke, Phys. Today, 39, No. 3, 36 (1986).
R. F. Voss et al., Proc. Second Intern. Conf. Superconducting Quantum Devices, Berlin (May, 1980), p. 94.
R. F. Voss et al., J. Appl. Phys., 51, 2306 (1980).
M. B. Ketchen and F. Voss, Appl. Phys. Lett., 35, 812 (1979).
J. Clarke, IEEE Trans. Electron. Dev., ED-27, 1896 (1980).
M. B. Ketchen and J. M. Jaycox, Appl. Phys. Lett., 40, 736 (1982).
J. M. Pierce, J. E. Opfer, and L. H. Rorden, IEEE Trans. Magn., MAG-10, 599 (1974).
P. Falferi, Class. Quantum Grav., 21, S973 (2004).
L. Gottardi et al., Class. Quantum Grav., 21, S1191 (2004).
M. Buhler and E. Umlauf, J. Low Temp. Phys., 93, 697 (1993).
T. Fausch, M. Buhler, and E. Umlauf, J. Low Temp. Phys., 93, 703 (1993).
R. Bandler et al., J. Low Temp. Phys., 93, 709 (1993).
O. V. Lounasmaa, Experimental Principles and Methods Below 1 K, Academic Press, London-New York (1974).
B. B. Schwartz and S. Foner (eds.), Superconductor Applications: Squids and Machines, Plenum Press, New York (1974).
L. D. Landau and E. M. Lifshits, Theoretical Physics. Vol. 5. Statistical Physics [in Russian], Fiz.-Mat. Lit., Moscow (1976).
R. P. Feynman, Statistical Mechanics, Addison-Wesley (1990).
M. J. Steenland, Thesis, Leiden (1952), p. 10.
M. J. Steenland, D. de Klerk, and C. J. Gorter, Leiden Commun. 284b; Physica, 15, 711 (1949).
A. I. Golovashkin et al., Kratkie Soobsh. Fizike, FIAN, Moscow, No. 10, 35 (2007).
E. R. Mueller and J. Walkman, www.aip.org/tip.INPHFA/vol-9/iss-4/p27.html.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Izmeritel'naya Tekhnika, No. 11, pp. 24–30, November, 2008.
Rights and permissions
About this article
Cite this article
Golovashkin, A.I., Zherikhina, L.N., Kuleshova, G.V. et al. Capabilities of a magnetic adiabatic calorimeter in measurement technology. Meas Tech 51, 1178–1187 (2008). https://doi.org/10.1007/s11018-009-9183-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11018-009-9183-9